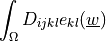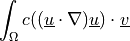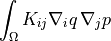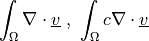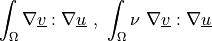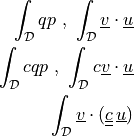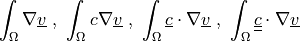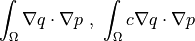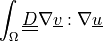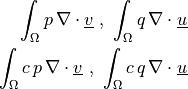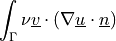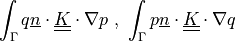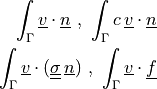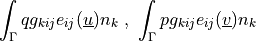Term Overview¶
Term Syntax¶
In general, the syntax of a term call is:
<term name>.<i>.<r>( <arg1>, <arg2>, ... ),
where <i> denotes an integral name (i.e. a name of numerical quadrature
to use) and <r> marks a region (domain of the integral).
The following notation is used:
symbol |
meaning |
|---|---|
|
cell (volume) (sub)domain |
|
facet (surface) (sub)domain |
|
cell or facet (sub)domain |
|
dimension of space |
|
time |
|
any function |
|
any vector function |
|
unit outward normal |
|
scalar test or parameter function |
|
scalar unknown or parameter function |
|
vector test or parameter function |
|
vector unknown or parameter function |
|
Cauchy strain tensor ( |
|
deformation gradient |
|
|
|
right Cauchy-Green deformation tensor |
|
Green strain tensor |
|
second Piola-Kirchhoff stress tensor |
|
vector volume forces |
|
scalar volume force (source) |
|
density |
|
kinematic viscosity |
|
any constant |
|
Kronecker delta, identity matrix |
|
trace of a second order tensor ( |
|
deviator of a second order tensor
( |
|
|
|
|
The suffix “ ” denotes a quantity related to a previous time step.
” denotes a quantity related to a previous time step.
Term names are (usually) prefixed according to the following conventions:
prefix |
meaning |
evaluation modes |
meaning |
|---|---|---|---|
dw |
discrete weak |
‘weak’ |
terms having a virtual (test) argument and zero or more unknown arguments, used for FE assembling |
ev |
evaluate |
‘eval’, ‘el_eval’, ‘el_avg’, ‘qp’ |
terms having all arguments known, modes ‘el_avg’, ‘qp’ are not supported by all ev_ terms |
de |
discrete einsum |
any (work in progress) |
multi-linear terms defined using an enriched einsum notation |
Evaluation modes ‘eval’, ‘el_avg’ and ‘qp’ are defined as follows:
mode |
definition |
|---|---|
‘eval’ |
|
‘el_avg’ |
vector for |
‘qp’ |
|
Term Table¶
Below we list all the terms available in automatically generated tables. The first column lists the name, the second column the argument lists and the third column the mathematical definition of each term. The terms are devided into the following tables:
Table of large deformation terms (total/updated Lagrangian formulation)
The notation <virtual> corresponds to a test function,
<state> to a unknown function and <parameter> to a known function. By
<material> we denote material (constitutive) parameters, or, in general, any
given function of space and time that parameterizes a term, for example
a given traction force vector.
Table of basic terms¶
name/class |
arguments |
definition |
examples |
|---|---|---|---|
dw_advect_div_free |
|
|
|
dw_bc_newton |
|
|
|
dw_biot |
|
|
bio.npb.lag, the.ela.ess, bio, the.ela, bio.npb, bio.sho.syn |
ev_biot_stress |
|
|
|
ev_cauchy_strain |
|
|
|
ev_cauchy_stress |
|
|
|
dw_contact |
|
|
|
dw_contact_ipc |
|
|
|
dw_contact_plane |
|
|
|
dw_contact_sphere |
|
|
|
dw_convect |
|
|
|
dw_convect_v_grad_s |
|
|
|
ev_def_grad |
|
|
|
dw_dg_advect_laxfrie_flux |
|
where
|
|
dw_dg_diffusion_flux |
|
where
|
|
dw_dg_interior_penalty |
|
where
|
|
dw_dg_nonlinear_laxfrie_flux |
|
where
|
|
dw_diffusion |
|
|
pie.ela, poi.neu, bio.npb.lag, bio, vib.aco, bio.npb, pie.ela, bio.sho.syn, dar.flo.mul |
dw_diffusion_coupling |
|
|
|
dw_diffusion_r |
|
|
|
ev_diffusion_velocity |
|
|
|
ev_div |
|
|
|
dw_div |
|
|
|
dw_div_grad |
|
|
|
dw_dot |
|
|
ref.evp, pie.ela, tim.hea.equ.mul.mat, vib.aco, poi.fun, tim.poi, sto.sli.bc, wel, hel.apa, aco, poi.per.bou.con, aco, dar.flo.mul, mod.ana.dec, tim.adv.dif, adv.1D, adv.2D, tim.poi.exp, lin.ela.up, the.ele, bor, pie.ela, hyd, bur.2D, lin.ela.dam, osc, bal |
dw_elastic_wave |
|
|
|
dw_elastic_wave_cauchy |
|
|
|
dw_electric_source |
|
|
|
ev_grad |
|
|
|
ev_integrate |
|
|
|
dw_integrate |
|
|
poi.neu, tim.hea.equ.mul.mat, hel.apa, aco, poi.per.bou.con, vib.aco, aco, dar.flo.mul |
ev_integrate_mat |
|
|
|
dw_jump |
|
|
|
dw_laplace |
|
|
ref.evp, cub, adv.dif.2D, tim.hea.equ.mul.mat, lap.flu.2d, vib.aco, poi.fie.dep.mat, lap.tim.ebc, poi.iga, poi.fun, tim.poi, sto.sli.bc, wel, lap.2D, hel.apa, aco, poi.per.bou.con, aco, lap.cou.lcb, tim.adv.dif, poi.sho.syn, tim.poi.exp, the.ele, bor, sin, hyd, lap.1d, the.ela.ess, bur.2D, osc, poi.par.stu, poi |
dw_lin_convect |
|
|
|
dw_lin_convect2 |
|
|
|
dw_lin_dspring |
|
|
|
dw_lin_dspring_rot |
|
|
|
dw_lin_elastic |
|
|
pie.ela, bio, nod.lcb, mix.mes, vib.aco, bio.npb, sei.loa, mat.non, com.ela.mat, tru.bri, mul.poi.con, lin.vis, pie.ela.mac, lin.ela.iga, its.1, ela.con.pla, lin.ela, its.3, mod.ana.dec, ela.shi.per, lin.ela.opt, lin.ela.up, bio.sho.syn, pie.ela, lin.ela.tra, lin.ela.mM, mul.nod.lcb, its.2, ela, bio.npb.lag, its.4, the.ela.ess, pre.fib, lin.ela.dam, the.ela, wed.mes, two.bod.con, ela.con.sph |
dw_lin_elastic_iso |
|
|
|
dw_lin_elastic_l_ad |
|
|
|
dw_lin_elastic_yp_ad |
|
|
|
dw_lin_prestress |
|
|
|
dw_lin_spring |
|
|
|
dw_lin_strain_fib |
|
|
|
dw_lin_truss |
|
|
|
ev_lin_truss_force |
|
|
|
dw_mass_ad |
|
|
|
dw_nl_diffusion |
|
|
|
dw_non_penetration |
|
|
|
dw_non_penetration_p |
|
|
|
dw_nonsym_elastic |
|
|
|
dw_ns_dot_grad_s |
|
|
|
dw_piezo_coupling |
|
|
|
ev_piezo_strain |
|
|
|
ev_piezo_stress |
|
|
|
dw_point_load |
|
|
|
dw_point_lspring |
|
|
|
dw_s_dot_grad_i_s |
|
|
|
dw_s_dot_mgrad_s |
|
|
|
dw_shell10x |
|
|
|
dw_stokes |
|
|
sta.nav.sto, nav.sto, lin.ela.up, nav.sto, nav.sto.iga, sto, sto.sli.bc |
dw_stokes_wave |
|
|
|
dw_stokes_wave_div |
|
|
|
ev_sum_vals |
|
||
ev_surface_flux |
|
|
|
dw_surface_flux |
|
|
|
dw_surface_ltr |
|
|
lin.vis, mix.mes, nod.lcb, lin.ela.opt, com.ela.mat, lin.ela.tra, wed.mes, ela.shi.per, tru.bri |
ev_surface_moment |
|
|
|
dw_surface_ndot |
|
|
|
ev_surface_piezo_flux |
|
|
|
dw_v_dot_grad_s |
|
|
|
dw_vm_dot_s |
|
|
|
ev_volume |
|
|
|
dw_volume_lvf |
|
|
|
dw_volume_nvf |
|
|
|
ev_volume_surface |
|
|
|
dw_zero |
|
|
Table of sensitivity terms¶
name/class |
arguments |
definition |
examples |
|---|---|---|---|
dw_adj_convect1 |
|
|
|
dw_adj_convect2 |
|
|
|
dw_adj_div_grad |
|
|
|
ev_sd_convect |
|
|
|
ev_sd_diffusion |
|
|
|
de_sd_diffusion |
|
|
|
ev_sd_div |
|
|
|
ev_sd_div_grad |
|
|
|
de_sd_div_grad |
|
|
|
ev_sd_dot |
|
|
|
de_sd_dot |
|
|
|
ev_sd_lin_elastic |
|
|
|
de_sd_lin_elastic |
|
|
|
de_sd_piezo_coupling |
|
|
|
ev_sd_piezo_coupling |
|
|
|
de_sd_stokes |
|
|
|
ev_sd_surface_integrate |
|
|
|
de_sd_surface_ltr |
|
|
|
ev_sd_surface_ltr |
|
|
|
de_sd_v_dot_grad_s |
|
|
Table of large deformation terms¶
name/class |
arguments |
definition |
examples |
|---|---|---|---|
dw_tl_bulk_active |
|
|
|
dw_tl_bulk_penalty |
|
|
|
dw_tl_bulk_pressure |
|
|
|
dw_tl_diffusion |
|
|
|
dw_tl_fib_a |
|
|
|
dw_tl_fib_e |
|
|
|
dw_tl_fib_spe |
|
|
|
dw_tl_he_genyeoh |
|
|
|
dw_tl_he_mooney_rivlin |
|
|
|
dw_tl_he_neohook |
|
|
act.fib, hyp, bal, per.tl, com.ela.mat |
dw_tl_he_neohook_ad |
|
|
|
dw_tl_he_ogden |
|
|
|
dw_tl_he_ogden_ad |
|
|
|
dw_tl_membrane |
|
||
ev_tl_surface_flux |
|
|
|
dw_tl_surface_traction |
|
|
|
dw_tl_volume |
|
|
|
ev_tl_volume_surface |
|
|
|
dw_ul_bulk_penalty |
|
|
|
dw_ul_bulk_pressure |
|
|
|
dw_ul_compressible |
|
|
|
dw_ul_he_by_fun |
|
|
|
dw_ul_he_mooney_rivlin |
|
|
|
dw_ul_he_neohook |
|
|
|
dw_ul_volume |
|
|
Table of special terms¶
name/class |
arguments |
definition |
examples |
|---|---|---|---|
dw_biot_eth |
|
|
|
dw_biot_th |
|
|
|
ev_cauchy_stress_eth |
|
|
|
ev_cauchy_stress_th |
|
|
|
dw_lin_elastic_eth |
|
|
|
dw_lin_elastic_th |
|
|
|
ev_of_ns_surf_min_d_press |
|
|
|
dw_of_ns_surf_min_d_press_diff |
|
|
|
ev_sd_st_grad_div |
|
|
|
ev_sd_st_pspg_c |
|
|
|
ev_sd_st_pspg_p |
|
|
|
ev_sd_st_supg_c |
|
|
|
dw_st_adj1_supg_p |
|
|
|
dw_st_adj2_supg_p |
|
|
|
dw_st_adj_supg_c |
|
|
|
dw_st_grad_div |
|
|
|
dw_st_pspg_c |
|
|
|
dw_st_pspg_p |
|
|
|
dw_st_supg_c |
|
|
|
dw_st_supg_p |
|
|
|
dw_volume_dot_w_scalar_eth |
|
|
|
dw_volume_dot_w_scalar_th |
|
|
Table of multi-linear terms¶
name/class |
arguments |
definition |
examples |
|---|---|---|---|
de_cauchy_stress |
|
|
|
de_convect |
|
|
|
de_diffusion |
|
|
|
de_div |
|
|
|
de_div_grad |
|
|
|
de_dot |
|
|
|
de_grad |
|
|
|
de_integrate |
|
|
|
de_laplace |
|
|
|
de_lin_convect |
|
|
|
de_lin_elastic |
|
|
|
de_m_flexo |
|
|
|
de_m_flexo_coupling |
|
|
|
de_m_sg_elastic |
|
|
|
de_mass |
|
|
|
de_non_penetration_p |
|
|
|
de_nonsym_elastic |
|
|
|
de_s_dot_mgrad_s |
|
|
|
de_stokes |
|
|
|
de_stokes_traction |
|
|
|
de_surface_flux |
|
|
|
de_surface_ltr |
|
|
|
de_surface_piezo_flux |
|
|
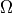
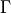
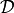
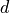
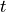
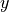
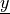
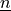
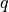


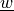 ,
, 
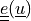
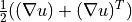 )
)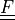
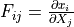
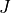
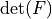
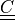
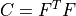
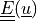
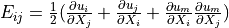
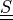
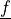
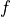
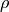
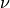
 ,
, 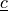 ,
, 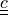
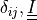
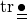
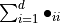 )
)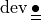
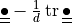 )
)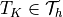
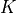 -th element of triangulation (= mesh)
-th element of triangulation (= mesh) 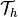 of
domain
of
domain 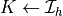
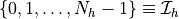 in ascending order
in ascending order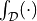
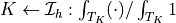
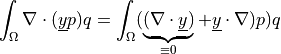
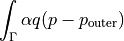
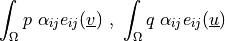


![\int_{\partial{T_K}} D \langle \nabla p \rangle [q] \mbox{
, } \int_{\partial{T_K}} D \langle \nabla q \rangle [p]](_images/math/40eee7c5fee7eeb0af0fee28f5caa69ecf49394d.png)
![[\phi] = \phi_{in} - \phi_{out}](_images/math/93f3b2071ecd9b131f2fd0d22b4c2801b4b86a5f.png)
![\int_{\partial{T_K}} \bar{D} C_w
\frac{Ord^2}{d(\partial{T_K})}[p][q]](_images/math/997ef0fcd99b567a45b72bdb9ac0675f11108038.png)
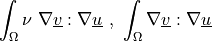
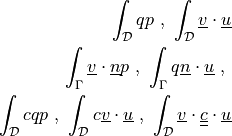
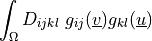
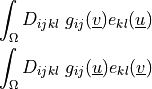
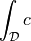
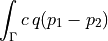
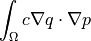
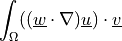
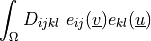
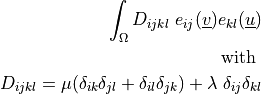
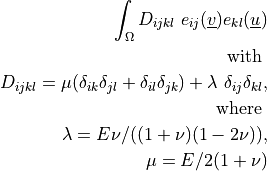
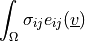
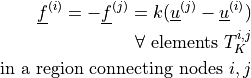
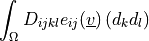
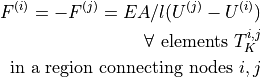
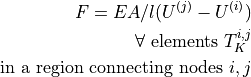
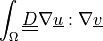
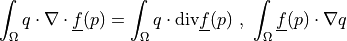
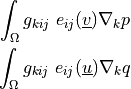
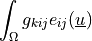
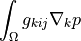
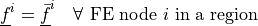
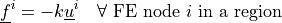
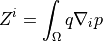
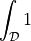

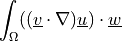
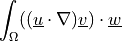
![\int_{\Omega} [ u_k \pdiff{u_i}{x_k} w_i (\nabla \cdot
\Vcal) - u_k \pdiff{\Vcal_j}{x_k} \pdiff{u_i}{x_j} w_i ]](_images/math/4c2921fc7c7deca6230f1ccba3f95f6b3605b4cb.png)
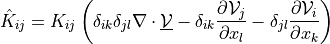
![\int_{\Omega} p [ (\nabla \cdot \ul{w}) (\nabla \cdot
\ul{\Vcal}) - \pdiff{\Vcal_k}{x_i} \pdiff{w_i}{x_k} ]](_images/math/874e29215a40bbd325c7face1df3c3751a4ba909.png)
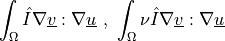
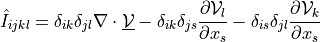
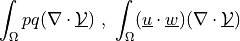
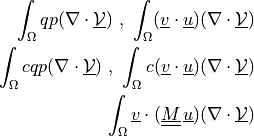
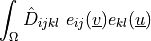
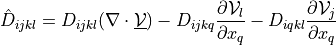
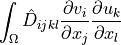
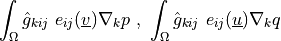
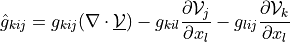
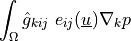
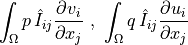
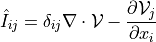
![\int_{\Gamma} \ul{v} \cdot
\left[\left(\ull{\hat{\sigma}}\, \nabla \cdot \ul{\cal{V}} -
\ull{{\hat\sigma}}\, \nabla \ul{\cal{V}} \right)\ul{n}\right]](_images/math/cc22dce1e0d84cbf47bee6ffbae8a983f9658ca7.png)
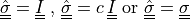
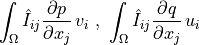
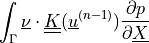
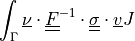
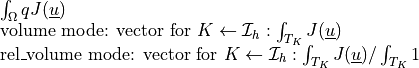
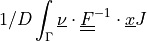
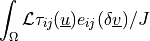
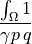
![\begin{array}{l} \int_{\Omega} \left [\int_0^t
\alpha_{ij}(t-\tau)\,p(\tau)) \difd{\tau} \right]\,e_{ij}(\ul{v})
\mbox{ ,} \\ \int_{\Omega} \left [\int_0^t \alpha_{ij}(t-\tau)
e_{kl}(\ul{u}(\tau)) \difd{\tau} \right] q \end{array}](_images/math/ae74335e72d41cd71f741f01a8e3d24d2546deb2.png)
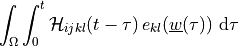
![\int_{\Omega} \left [\int_0^t
\Hcal_{ijkl}(t-\tau)\,e_{kl}(\ul{u}(\tau)) \difd{\tau}
\right]\,e_{ij}(\ul{v})](_images/math/e8480ee3ec2210daf9504fe05bc9e759bfd97e14.png)
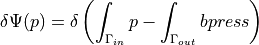
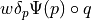
![\gamma \int_{\Omega} [ (\nabla \cdot \ul{u}) (\nabla \cdot
\ul{w}) (\nabla \cdot \ul{\Vcal}) - \pdiff{u_i}{x_k}
\pdiff{\Vcal_k}{x_i} (\nabla \cdot \ul{w}) - (\nabla \cdot \ul{u})
\pdiff{w_i}{x_k} \pdiff{\Vcal_k}{x_i} ]](_images/math/1d993de9a7a8fddb21c9dabe827b673d836a84fd.png)
![\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ [ \pdiff{r}{x_i}
(\ul{b} \cdot \nabla u_i) (\nabla \cdot \Vcal) - \pdiff{r}{x_k}
\pdiff{\Vcal_k}{x_i} (\ul{b} \cdot \nabla u_i) - \pdiff{r}{x_k}
(\ul{b} \cdot \nabla \Vcal_k) \pdiff{u_i}{x_k} ]](_images/math/302dfa868e9ae2d47ded773ed48c621272b2cc79.png)
![\sum_{K \in \Ical_h}\int_{T_K} \tau_K\ [ (\nabla r \cdot
\nabla p) (\nabla \cdot \Vcal) - \pdiff{r}{x_k} (\nabla \Vcal_k
\cdot \nabla p) - (\nabla r \cdot \nabla \Vcal_k) \pdiff{p}{x_k} ]](_images/math/4aacda02e8f0f40c57b55a38ddb8eea832031d68.png)
![\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ [ (\ul{b} \cdot
\nabla u_k) (\ul{b} \cdot \nabla w_k) (\nabla \cdot \Vcal) -
(\ul{b} \cdot \nabla \Vcal_i) \pdiff{u_k}{x_i} (\ul{b} \cdot
\nabla w_k) - (\ul{u} \cdot \nabla u_k) (\ul{b} \cdot \nabla
\Vcal_i) \pdiff{w_k}{x_i} ]](_images/math/ab76e6b282a0a506b5418ba1f82c29ef97a1a394.png)
![\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ [ ((\ul{v} \cdot
\nabla) \ul{u}) ((\ul{u} \cdot \nabla) \ul{w}) + ((\ul{u} \cdot
\nabla) \ul{u}) ((\ul{v} \cdot \nabla) \ul{w}) ]](_images/math/92142b1b6d83ed0bfc672b7ef9fb207b2846f157.png)
![\int_\Omega \left [\int_0^t \Gcal(t-\tau) p(\tau)
\difd{\tau} \right] q](_images/math/e6b2ee8fc64b715209b0f9d6699194157d31e048.png)