linear_elasticity/modal_analysis_declarative.py¶
Description
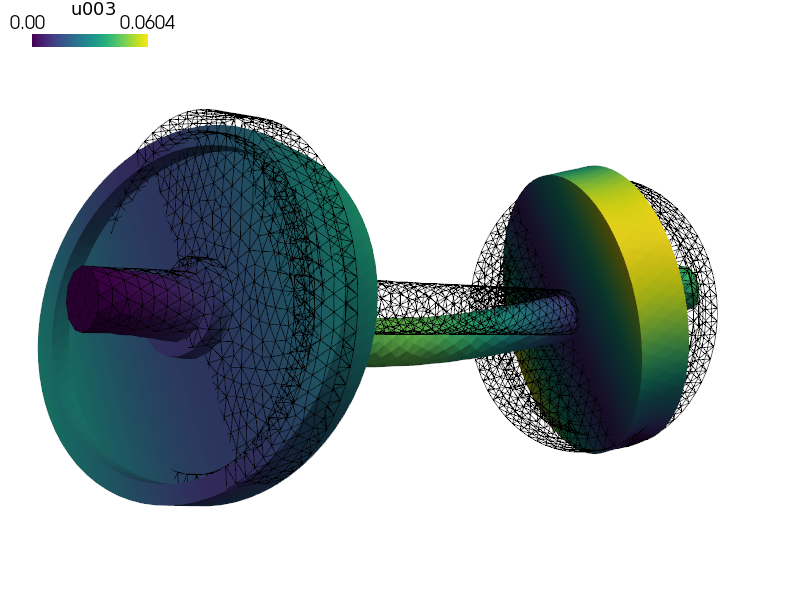
Modal analysis of a wheel set.
The first six modes are the rigid body modes because no boundary conditions are applied.
Running the simulation:
sfepy-run sfepy/examples/linear_elasticity/modal_analysis_declarative.py
The eigenvalues are saved to wheelset_eigs.txt and the eigenvectros to wheelset.vtk. View the results using:
sfepy-view wheelset.vtk -f u003:wu003:f30%:p0 1:vw:p0
The first six frequencies calculated by SfePy:
[11.272, 11.322, 34.432, 80.711, 80.895, 93.149]
The results of modal analysis performed in Ansys:
[11.306, 11.316, 34.486, 80.901, 81.139, 93.472]
"""
Modal analysis of a wheel set.
The first six modes are the rigid body modes because no boundary
conditions are applied.
Running the simulation::
sfepy-run sfepy/examples/linear_elasticity/modal_analysis_declarative.py
The eigenvalues are saved to wheelset_eigs.txt and the eigenvectros to
wheelset.vtk. View the results using::
sfepy-view wheelset.vtk -f u003:wu003:f30%:p0 1:vw:p0
The first six frequencies calculated by SfePy::
[11.272, 11.322, 34.432, 80.711, 80.895, 93.149]
The results of modal analysis performed in Ansys::
[11.306, 11.316, 34.486, 80.901, 81.139, 93.472]
"""
import numpy as nm
from sfepy.base.base import output
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy import data_dir
def report_eigs(pb, evp):
eigs = evp.eigs
n_rbm = evp.pb.conf.n_rbm
output('%d eigenvalues converged (%d ignored as rigid body modes)' %
(len(eigs), n_rbm))
eigs = eigs[n_rbm:]
omegas = nm.sqrt(eigs)
freqs = omegas / (2 * nm.pi)
output('number | eigenvalue | angular frequency '
'| frequency')
for ii, eig in enumerate(eigs):
output('%6d | %17.12e | %17.12e | %17.12e'
% (ii + 1, eig, omegas[ii], freqs[ii]))
def define(n_eigs=6, approx_order=1, density=7850., young=210e9, poisson=0.3):
filename_mesh, dim = data_dir + '/meshes/3d/wheelset.vtk', 3
n_rbm = 0
options = {
'n_eigs': n_eigs + n_rbm,
'eigs_only': False,
'post_process_hook_final': 'report_eigs',
'evps': 'eig',
}
regions = {
'Omega': 'all',
'Fix': ('vertices in (x < -1.08999)', 'vertex'),
}
materials = {
'm': ({
'D': stiffness_from_youngpoisson(dim, young, poisson),
'rho': density,
},),
}
fields = {
'displacement': ('real', 'vector', 'Omega', approx_order),
}
variables = {
'u': ('unknown field', 'displacement'),
'v': ('test field', 'displacement', 'u'),
}
integrals = {
'i': 2 * approx_order,
}
equations = {
'lhs': 'dw_lin_elastic.i.Omega(m.D, v, u)',
'rhs': 'dw_dot.i.Omega(m.rho, v, u)',
}
ebcs = {
'fix': ('Fix', {'u.all': 0.0}) # fix rigid body modes
}
solvers = {
# 'eig': ('eig.matlab', {
# 'method': 'eigs',
# 'which': 'sm',
# 'eps': 1e-6,
# }),
#'eig': ('eig.primme', {
# 'which': 'SM',
# 'tol': 1e-8,
#}),
'eig': ('eig.scipy', {
'method': 'eigsh',
'which': 'LM',
'sigma': 0,
'tol': 1e-8,
'linear_solver': ('ls.scipy_superlu', {}),
# 'linear_solver': ('ls.cholesky', {}),
# 'linear_solver': ('ls.mumps', {}),
# 'ls.cholesky' and 'ls.mumps' linear solvers are much faster,
# but scikit-sparse package and MUMPS library are required
'maxiter': 1000,
}),
}
return locals()