linear_elasticity/modal_analysis.py¶
Description
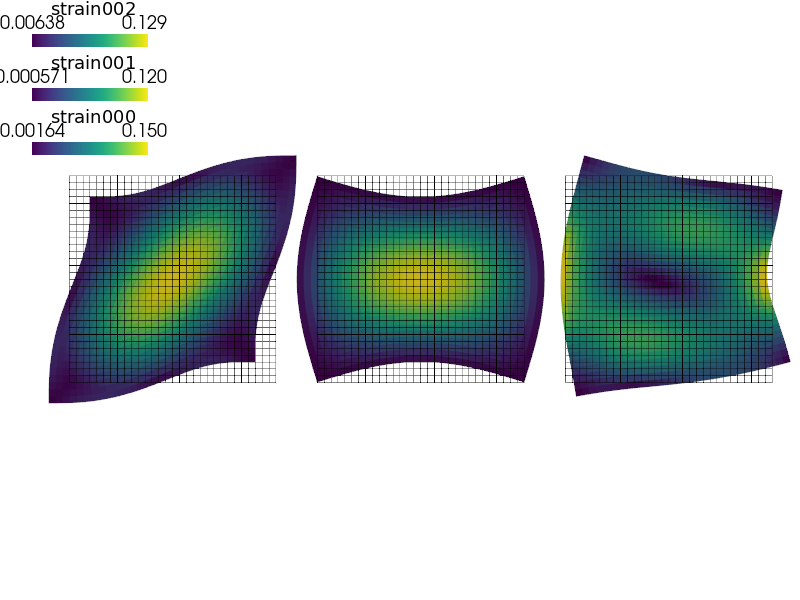
Modal analysis of a linear elastic block in 2D or 3D.
The dimension of the problem is determined by the length of the vector
in --dims option.
Optionally, a mesh file name can be given as a positional argument. In that case, the mesh generation options are ignored.
The default material properties correspond to aluminium in the following units:
length: m
mass: kg
stiffness / stress: Pa
density: kg / m^3
Examples¶
Run with the default arguments:
python sfepy/examples/linear_elasticity/modal_analysis.py
Fix bottom surface of the domain:
python sfepy/examples/linear_elasticity/modal_analysis.py -b cantilever
Increase mesh resolution:
python sfepy/examples/linear_elasticity/modal_analysis.py -s 31,31
Use 3D domain:
python sfepy/examples/linear_elasticity/modal_analysis.py -d 1,1,1 -c 0,0,0 -s 8,8,8
Change the eigenvalue problem solver to LOBPCG:
python sfepy/examples/linear_elasticity/modal_analysis.py --solver="eig.scipy_lobpcg,i_max:100,largest:False"
See
sfepy.solvers.eigenfor available solvers.
#!/usr/bin/env python
"""
Modal analysis of a linear elastic block in 2D or 3D.
The dimension of the problem is determined by the length of the vector
in ``--dims`` option.
Optionally, a mesh file name can be given as a positional argument. In that
case, the mesh generation options are ignored.
The default material properties correspond to aluminium in the following units:
- length: m
- mass: kg
- stiffness / stress: Pa
- density: kg / m^3
Examples
--------
- Run with the default arguments::
python sfepy/examples/linear_elasticity/modal_analysis.py
- Fix bottom surface of the domain::
python sfepy/examples/linear_elasticity/modal_analysis.py -b cantilever
- Increase mesh resolution::
python sfepy/examples/linear_elasticity/modal_analysis.py -s 31,31
- Use 3D domain::
python sfepy/examples/linear_elasticity/modal_analysis.py -d 1,1,1 -c 0,0,0 -s 8,8,8
- Change the eigenvalue problem solver to LOBPCG::
python sfepy/examples/linear_elasticity/modal_analysis.py --solver="eig.scipy_lobpcg,i_max:100,largest:False"
See :mod:`sfepy.solvers.eigen` for available solvers.
"""
import sys
sys.path.append('.')
from argparse import ArgumentParser, RawDescriptionHelpFormatter
import numpy as nm
import scipy.sparse.linalg as sla
from sfepy.base.base import assert_, output, Struct
from sfepy.discrete import (FieldVariable, Material, Integral, Integrals,
Equation, Equations, Problem)
from sfepy.discrete.fem import Mesh, FEDomain, Field
from sfepy.terms import Term
from sfepy.discrete.conditions import Conditions, EssentialBC
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy.mesh.mesh_generators import gen_block_mesh
from sfepy.solvers import Solver
helps = {
'dims' :
'dimensions of the block [default: %(default)s]',
'centre' :
'centre of the block [default: %(default)s]',
'shape' :
'numbers of vertices along each axis [default: %(default)s]',
'bc_kind' :
'kind of Dirichlet boundary conditions on the bottom and top surfaces,'
' one of: free, cantilever, fixed [default: %(default)s]',
'axis' :
'the axis index of the block that the bottom and top surfaces are related'
' to [default: %(default)s]',
'young' : "the Young's modulus [default: %(default)s]",
'poisson' : "the Poisson's ratio [default: %(default)s]",
'density' : "the material density [default: %(default)s]",
'order' : 'displacement field approximation order [default: %(default)s]',
'n_eigs' : 'the number of eigenvalues to compute [default: %(default)s]',
'ignore' : 'if given, the number of eigenvalues to ignore (e.g. rigid'
' body modes); has precedence over the default setting determined by'
' --bc-kind [default: %(default)s]',
'solver' : 'the eigenvalue problem solver to use. It should be given'
' as a comma-separated list: solver_kind,option0:value0,option1:value1,...'
' [default: %(default)s]',
}
def main():
parser = ArgumentParser(description=__doc__,
formatter_class=RawDescriptionHelpFormatter)
parser.add_argument('--version', action='version', version='%(prog)s')
parser.add_argument('-d', '--dims', metavar='dims',
action='store', dest='dims',
default='[1.0, 1.0]', help=helps['dims'])
parser.add_argument('-c', '--centre', metavar='centre',
action='store', dest='centre',
default='[0.0, 0.0]', help=helps['centre'])
parser.add_argument('-s', '--shape', metavar='shape',
action='store', dest='shape',
default='[11, 11]', help=helps['shape'])
parser.add_argument('-b', '--bc-kind', metavar='kind',
action='store', dest='bc_kind',
choices=['free', 'cantilever', 'fixed'],
default='free', help=helps['bc_kind'])
parser.add_argument('-a', '--axis', metavar='0, ..., dim, or -1',
type=int, action='store', dest='axis',
default=-1, help=helps['axis'])
parser.add_argument('--young', metavar='float', type=float,
action='store', dest='young',
default=6.80e+10, help=helps['young'])
parser.add_argument('--poisson', metavar='float', type=float,
action='store', dest='poisson',
default=0.36, help=helps['poisson'])
parser.add_argument('--density', metavar='float', type=float,
action='store', dest='density',
default=2700.0, help=helps['density'])
parser.add_argument('--order', metavar='int', type=int,
action='store', dest='order',
default=1, help=helps['order'])
parser.add_argument('-n', '--n-eigs', metavar='int', type=int,
action='store', dest='n_eigs',
default=6, help=helps['n_eigs'])
parser.add_argument('-i', '--ignore', metavar='int', type=int,
action='store', dest='ignore',
default=None, help=helps['ignore'])
parser.add_argument('--solver', metavar='solver', action='store',
dest='solver',
default= \
"eig.scipy,method:'eigsh',tol:1e-5,maxiter:1000",
help=helps['solver'])
parser.add_argument('filename', nargs='?', default=None)
options = parser.parse_args()
aux = options.solver.split(',')
kwargs = {}
for option in aux[1:]:
key, val = option.split(':')
kwargs[key.strip()] = eval(val)
eig_conf = Struct(name='evp', kind=aux[0], **kwargs)
output('using values:')
output(" Young's modulus:", options.young)
output(" Poisson's ratio:", options.poisson)
output(' density:', options.density)
output('displacement field approximation order:', options.order)
output('requested %d eigenvalues' % options.n_eigs)
output('using eigenvalue problem solver:', eig_conf.kind)
output.level += 1
for key, val in kwargs.items():
output('%s: %r' % (key, val))
output.level -= 1
assert_((0.0 < options.poisson < 0.5),
"Poisson's ratio must be in ]0, 0.5[!")
assert_((0 < options.order),
'displacement approximation order must be at least 1!')
filename = options.filename
if filename is not None:
mesh = Mesh.from_file(filename)
dim = mesh.dim
dims = nm.diff(mesh.get_bounding_box(), axis=0)
else:
dims = nm.array(eval(options.dims), dtype=nm.float64)
dim = len(dims)
centre = nm.array(eval(options.centre), dtype=nm.float64)[:dim]
shape = nm.array(eval(options.shape), dtype=nm.int32)[:dim]
output('dimensions:', dims)
output('centre: ', centre)
output('shape: ', shape)
mesh = gen_block_mesh(dims, shape, centre, name='mesh')
output('axis: ', options.axis)
assert_((-dim <= options.axis < dim), 'invalid axis value!')
eig_solver = Solver.any_from_conf(eig_conf)
# Build the problem definition.
domain = FEDomain('domain', mesh)
bbox = domain.get_mesh_bounding_box()
min_coor, max_coor = bbox[:, options.axis]
eps = 1e-8 * (max_coor - min_coor)
ax = 'xyz'[:dim][options.axis]
omega = domain.create_region('Omega', 'all')
bottom = domain.create_region('Bottom',
'vertices in (%s < %.10f)'
% (ax, min_coor + eps),
'facet')
bottom_top = domain.create_region('BottomTop',
'r.Bottom +v vertices in (%s > %.10f)'
% (ax, max_coor - eps),
'facet')
field = Field.from_args('fu', nm.float64, 'vector', omega,
approx_order=options.order)
u = FieldVariable('u', 'unknown', field)
v = FieldVariable('v', 'test', field, primary_var_name='u')
mtx_d = stiffness_from_youngpoisson(dim, options.young, options.poisson)
m = Material('m', D=mtx_d, rho=options.density)
integral = Integral('i', order=2*options.order)
t1 = Term.new('dw_lin_elastic(m.D, v, u)', integral, omega, m=m, v=v, u=u)
t2 = Term.new('dw_dot(m.rho, v, u)', integral, omega, m=m, v=v, u=u)
eq1 = Equation('stiffness', t1)
eq2 = Equation('mass', t2)
lhs_eqs = Equations([eq1, eq2])
pb = Problem('modal', equations=lhs_eqs)
if options.bc_kind == 'free':
pb.time_update()
n_rbm = dim * (dim + 1) // 2
elif options.bc_kind == 'cantilever':
fixed = EssentialBC('Fixed', bottom, {'u.all' : 0.0})
pb.time_update(ebcs=Conditions([fixed]))
n_rbm = 0
elif options.bc_kind == 'fixed':
fixed = EssentialBC('Fixed', bottom_top, {'u.all' : 0.0})
pb.time_update(ebcs=Conditions([fixed]))
n_rbm = 0
else:
raise ValueError('unsupported BC kind! (%s)' % options.bc_kind)
if options.ignore is not None:
n_rbm = options.ignore
pb.update_materials()
# Assemble stiffness and mass matrices.
mtx_k = eq1.evaluate(mode='weak', dw_mode='matrix', asm_obj=pb.mtx_a)
mtx_m = mtx_k.copy()
mtx_m.data[:] = 0.0
mtx_m = eq2.evaluate(mode='weak', dw_mode='matrix', asm_obj=mtx_m)
try:
eigs, svecs = eig_solver(mtx_k, mtx_m, options.n_eigs + n_rbm,
eigenvectors=True)
except sla.ArpackNoConvergence as ee:
eigs = ee.eigenvalues
svecs = ee.eigenvectors
output('only %d eigenvalues converged!' % len(eigs))
output('%d eigenvalues converged (%d ignored as rigid body modes)' %
(len(eigs), n_rbm))
eigs = eigs[n_rbm:]
svecs = svecs[:, n_rbm:]
omegas = nm.sqrt(eigs)
freqs = omegas / (2 * nm.pi)
output('number | eigenvalue | angular frequency '
'| frequency')
for ii, eig in enumerate(eigs):
output('%6d | %17.12e | %17.12e | %17.12e'
% (ii + 1, eig, omegas[ii], freqs[ii]))
# Make full eigenvectors (add DOFs fixed by boundary conditions).
variables = pb.set_default_state()
vecs = nm.empty((variables.di.n_dof_total, svecs.shape[1]),
dtype=nm.float64)
for ii in range(svecs.shape[1]):
vecs[:, ii] = variables.make_full_vec(svecs[:, ii])
# Save the eigenvectors.
out = {}
for ii in range(eigs.shape[0]):
variables.set_state(vecs[:, ii])
aux = variables.create_output()
strain = pb.evaluate('ev_cauchy_strain.i.Omega(u)',
integrals=Integrals([integral]),
mode='el_avg', verbose=False)
out['u%03d' % ii] = aux.popitem()[1]
out['strain%03d' % ii] = Struct(mode='cell', data=strain)
pb.save_state('eigenshapes.vtk', out=out)
pb.save_regions_as_groups('regions')
if __name__ == '__main__':
main()