multi_physics/piezo_elasticity_macro.py

Description

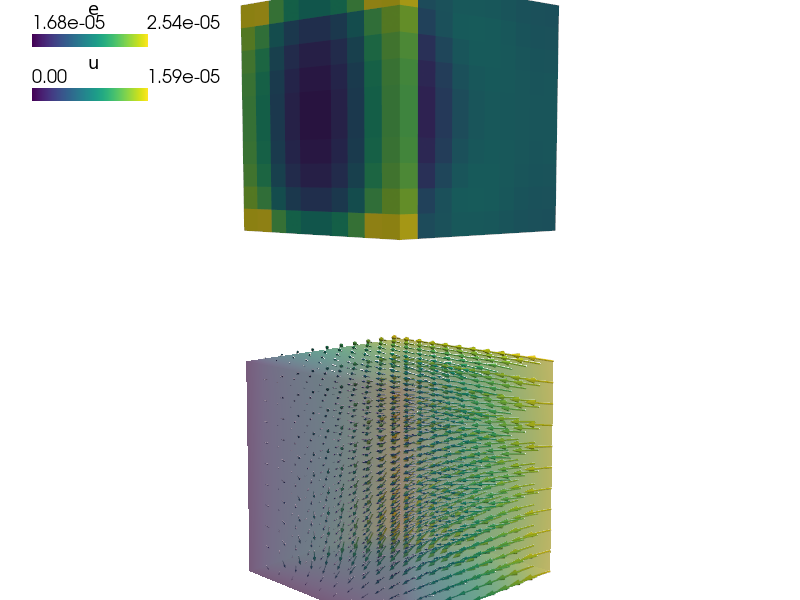
Piezo-elasticity problem - homogenization of a piezoelectric linear elastic matrix with embedded metalic electrodes, see [1] for details.

[1] E.Rohan, V.Lukes: Homogenization of the fluid-saturated piezoelectric porous media. International Journal of Solids and Structures 147, 2018, pages 110-125. https://doi.org/10.1016/j.ijsolstr.2018.05.017

source code

r"""
Piezo-elasticity problem - homogenization of a piezoelectric linear elastic
matrix with embedded metalic electrodes, see [1] for details.

[1] E.Rohan, V.Lukes: Homogenization of the fluid-saturated piezoelectric
porous media. International Journal of Solids and Structures 147, 2018,
pages 110-125. https://doi.org/10.1016/j.ijsolstr.2018.05.017
"""

import numpy as nm
from sfepy import data_dir, base_dir
from sfepy.base.base import Struct
from sfepy.homogenization.micmac import get_homog_coefs_linear
import os.path as osp
from sfepy.homogenization.recovery import recover_micro_hook


def post_process(out, pb, state, extend=False):
    # evaluate macroscopic strain
    strain = pb.evaluate('ev_cauchy_strain.i2.Omega(u)', mode='el_avg')
    out['e'] = Struct(name='output_data', mode='cell', dofs=None,
                      var_name='u', data=strain)

    # micro recovery
    rreg = pb.domain.regions['Recovery']
    dim = rreg.dim

    state_dict = state.get_state_parts()
    displ = state_dict['u']

    displ = displ.reshape((displ.shape[0] // dim, dim))
    macro = {
        'u': ('val', 'svar', displ),
        'strain': ('cauchy_strain', 'svar', displ),
        '_phi': pb.conf.phi,
    }

    def_args = {
        'eps0': pb.conf.eps0,
        'filename_mesh': pb.conf.filename_mesh_micro,
    }

    pvar = pb.create_variables(['svar'])

    recover_micro_hook(pb.conf.filename_micro, rreg, macro, pb.conf.eps0,
                       region_mode=pb.conf.region_mode,
                       eval_mode=pb.conf.eval_mode,
                       eval_vars=pvar, define_args=def_args)

    return out


def get_homog_fun(fname):
    return lambda ts, coors, mode=None, problem=None, **kwargs:\
        get_homog(coors, mode, problem, fname, **kwargs)


def get_homog(coors, mode, pb, micro_filename, **kwargs):
    if not (mode == 'qp'):
        return

    nqp = coors.shape[0]
    coefs_filename = osp.join(pb.conf.options.get('output_dir', '.'),
                              'coefs_piezo.h5')

    def_args = {
        'eps0': pb.conf.eps0,
        'filename_mesh': pb.conf.filename_mesh_micro,
    }

    coefs = get_homog_coefs_linear(0, 0, None,
                                   micro_filename=micro_filename,
                                   coefs_filename=coefs_filename,
                                   define_args=def_args)

    Vf = coefs['V0'] * pb.conf.phi[0] + coefs['V1'] * pb.conf.phi[1]

    out = {
        'A': nm.tile(coefs['A'], (nqp, 1, 1)),
        'Vf': nm.tile(Vf[:, nm.newaxis], (nqp, 1, 1)),
    }

    return out


def define(region_mode='el_centers', eval_mode='constant'):
    """
    Parameters
    ----------
    region_mode : {'el_centers', 'tiled')
    eval_mode : {'constant', 'continuous'}
    """
    eps0 = 1. / 30  # real size of the reference cell

    phi = nm.array([1, -1]) * 1e4  # prescribed el. potential

    filename_mesh = data_dir + '/meshes/3d/cube_medium_hexa.mesh'

    # define the micro problem - homogenization procedure
    filename_micro = base_dir +\
        '/examples/multi_physics/piezo_elasticity_micro.py'
    filename_mesh_micro = data_dir + '/meshes/3d/piezo_mesh_micro.vtk'

    fields = {
        'displacement': ('real', 'vector', 'Omega', 1),
        'sfield': ('real', 'scalar', 'Omega', 1),
    }

    variables = {
        'u': ('unknown field', 'displacement'),
        'v': ('test field', 'displacement', 'u'),
        'svar': ('parameter field', 'sfield', 'set-to-none'),
    }

    # define material - homogenization
    functions = {
        'get_homog': (get_homog_fun(filename_micro),),
    }

    materials = {
        'hom': 'get_homog',
    }

    integrals = {
        'i2': 2,
    }

    regions = {
        'Omega': 'all',
        'Left': ('vertices in (x < -0.4999)', 'facet'),
        'Recovery': ('cell 266'),
    }

    ebcs = {
        'fixed_u': ('Left', {'u.all': 0.0}),
    }

    equations = {
        'balance_of_forces': """
            dw_lin_elastic.i2.Omega(hom.A, v, u)
          =
          - dw_lin_prestress.i2.Omega(hom.Vf, v)""",
    }

    solvers = {
        'ls': ('ls.scipy_direct', {}),
        'newton': ('nls.newton',
                   {'i_max': 10,
                    'eps_a': 1e-3,
                    'eps_r': 1e-3,
                    'problem': 'nonlinear',
                    })
    }

    options = {
        'output_dir': 'output',
        'nls': 'newton',
        'post_process_hook': 'post_process',
    }

    return locals()