diffusion/laplace_1d.py¶
Description
Laplace equation in 1D with a variable coefficient.
Because the mesh is trivial in 1D, it is generated by mesh_hook(), and
registered using UserMeshIO.
Find 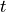 such that:
such that:
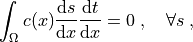
where the coefficient 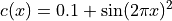 is computed in
is computed in
get_coef().
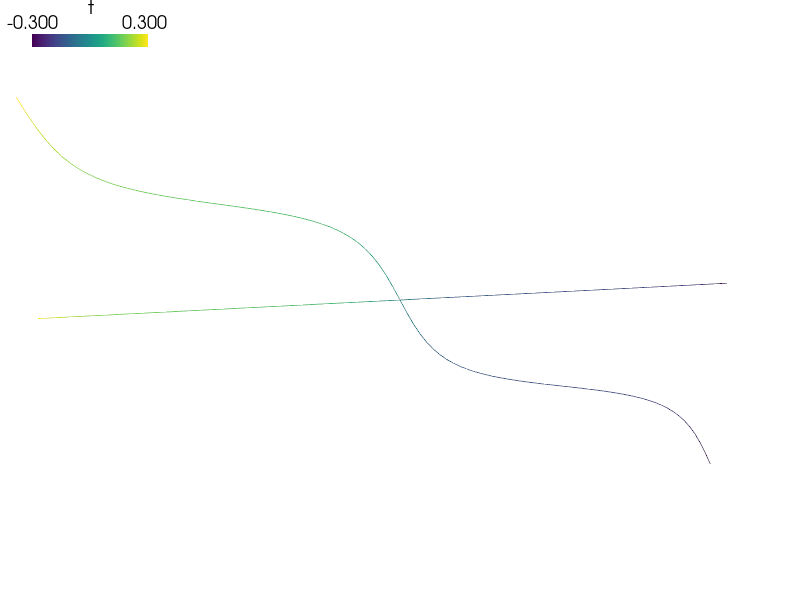
View the results using:
sfepy-view laplace_1d.vtk -f t:wt 1:vw
r"""
Laplace equation in 1D with a variable coefficient.
Because the mesh is trivial in 1D, it is generated by :func:`mesh_hook()`, and
registered using :class:`UserMeshIO <sfepy.discrete.fem.meshio.UserMeshIO>`.
Find :math:`t` such that:
.. math::
\int_{\Omega} c(x) \tdiff{s}{x} \tdiff{t}{x}
= 0
\;, \quad \forall s \;,
where the coefficient :math:`c(x) = 0.1 + \sin(2 \pi x)^2` is computed in
:func:`get_coef()`.
View the results using::
sfepy-view laplace_1d.vtk -f t:wt 1:vw
"""
import numpy as nm
from sfepy.discrete.fem import Mesh
from sfepy.discrete.fem.meshio import UserMeshIO
def mesh_hook(mesh, mode):
"""
Generate the 1D mesh.
"""
if mode == 'read':
n_nod = 101
coors = nm.linspace(0.0, 1.0, n_nod).reshape((n_nod, 1))
conn = nm.arange(n_nod, dtype=nm.int32).repeat(2)[1:-1].reshape((-1, 2))
mat_ids = nm.zeros(n_nod - 1, dtype=nm.int32)
descs = ['1_2']
mesh = Mesh.from_data('laplace_1d', coors, None,
[conn], [mat_ids], descs)
return mesh
elif mode == 'write':
pass
def get_coef(ts, coors, mode=None, **kwargs):
if mode == 'qp':
x = coors[:, 0]
val = 0.1 + nm.sin(2 * nm.pi * x)**2
val.shape = (coors.shape[0], 1, 1)
return {'val' : val}
filename_mesh = UserMeshIO(mesh_hook)
materials = {
'coef' : 'get_coef',
}
functions = {
'get_coef' : (get_coef,),
}
regions = {
'Omega' : 'all',
'Gamma_Left' : ('vertices in (x < 0.00001)', 'facet'),
'Gamma_Right' : ('vertices in (x > 0.99999)', 'facet'),
}
fields = {
'temperature' : ('real', 1, 'Omega', 1),
}
variables = {
't' : ('unknown field', 'temperature', 0),
's' : ('test field', 'temperature', 't'),
}
ebcs = {
't1' : ('Gamma_Left', {'t.0' : 0.3}),
't2' : ('Gamma_Right', {'t.0' : -0.3}),
}
integrals = {
'i' : 2,
}
equations = {
'Temperature' : """dw_laplace.i.Omega(coef.val, s, t) = 0"""
}
solvers = {
'ls' : ('ls.scipy_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 1,
'eps_a' : 1e-10,
}),
}
options = {
'nls' : 'newton',
'ls' : 'ls',
}