linear_elasticity/linear_elastic_iga.py¶
Description
Linear elasticity solved in a single patch NURBS domain using the isogeometric analysis (IGA) approach.
Find  such that:
such that:
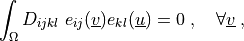
where
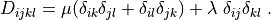
The domain geometry was created by:
sfepy-mesh iga-patch -d [1,0.5,0.1] -s [11,5,3] --degrees [2,2,2] -o meshes/iga/block3d.iga
View the results using:
sfepy-view block3d.vtk -f u:wu 1:vw

r"""
Linear elasticity solved in a single patch NURBS domain using the isogeometric
analysis (IGA) approach.
Find :math:`\ul{u}` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
= 0
\;, \quad \forall \ul{v} \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
The domain geometry was created by::
sfepy-mesh iga-patch -d [1,0.5,0.1] -s [11,5,3] --degrees [2,2,2] -o meshes/iga/block3d.iga
View the results using::
sfepy-view block3d.vtk -f u:wu 1:vw
"""
from sfepy.mechanics.matcoefs import stiffness_from_lame
from sfepy import data_dir
filename_domain = data_dir + '/meshes/iga/block3d.iga'
regions = {
'Omega' : 'all',
'Gamma1' : ('vertices of set xi00', 'facet'),
'Gamma2' : ('vertices of set xi01', 'facet'),
}
materials = {
'solid' : ({
'D' : stiffness_from_lame(3, lam=5.769, mu=3.846),
},),
}
fields = {
'displacement': ('real', 'vector', 'Omega', None, 'H1', 'iga'),
}
integrals = {
'i' : 3,
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
}
ebcs = {
'u1' : ('Gamma1', {'u.all' : 0.0}),
'u2' : ('Gamma2', {'u.0' : 0.1, 'u.[1,2]' : 'get_ebcs'}),
}
def get_ebcs(ts, coors, **kwargs):
import numpy as nm
aux = nm.empty_like(coors[:, 1:])
aux[:, 0] = 0.1 * coors[:, 1]
aux[:, 1] = -0.05 + 0.03 * nm.sin(coors[:, 1] * 5 * nm.pi)
return aux
functions = {
'get_ebcs' : (get_ebcs,),
}
equations = {
'balance_of_forces' : """dw_lin_elastic.i.Omega(solid.D, v, u) = 0""",
}
solvers = {
'ls' : ('ls.scipy_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 1,
'eps_a' : 1e-10,
}),
}