dg/laplace_2D.py

Description

Laplace equation solved in 2d by discontinous Galerkin method

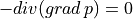
on rectangle

p = 0 p_y = 0

[0,b]—————————–[a, b]

|

|

p_x = -a | p(x,y) | p_x = 0 p = 0 | | p = 0

|

[0,0]—————————–[a, 0]

p_y = b p = 0

solution to this is

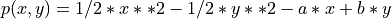
Usage Examples

Run:

sfepy-run sfepy/examples/dg/laplace_2D.py

Results are saved to output/dg/laplace_2D folder by default as .msh files, the best way to view them is through GMSH (http://gmsh.info/) version 4.6 or newer. Start GMSH and use File | Open menu or Crtl + O shortcut, navigate to the output folder, select all .msh files and hit Open, all files should load as one item in Post-processing named p_cell_nodes.

GMSH is capable of rendering high order approximations in individual elements, to modify fidelity of rendering, double click the displayed mesh, quick options menu should pop up, click on All view options.... This brings up the Options window with View [0] selected in left column. Under the tab General ensure that Adapt visualization grid is ticked, then you can adjust Maximum recursion depth and `Target visualization error to tune the visualization. To see visualization elements (as opposed to mesh elements) go to Visibility tab and tick Draw element outlines, this option is also available from quick options menu as View element outlines or under shortcut Alt+E. In the quick options menu, you can also modify normal raise by clicking View Normal Raise to see solution rendered as surface above the mesh. Note that for triangular meshes normal raise -1 produces expected raise above the mesh. This is due to the opposite orientation of the reference elements in GMSH and Sfepy and might get patched in the future.

source code

r"""
Laplace equation solved in 2d by discontinous Galerkin method

.. math:: - div(grad\,p) = 0

on rectangle
                    p = 0
                    p_y = 0
    [0,b]-----------------------------[a, b]
         |                           |
         |                           |
p_x = -a |         p(x,y)            | p_x = 0
p = 0    |                           | p = 0
         |                           |
    [0,0]-----------------------------[a, 0]
                    p_y = b
                    p = 0

solution to this is
   .. math:: p(x,y) = 1/2*x**2 - 1/2*y**2 - a*x + b*y


Usage Examples
--------------

Run::

  sfepy-run sfepy/examples/dg/laplace_2D.py

Results are saved to output/dg/laplace_2D folder by default as ``.msh`` files,
the best way to view them is through GMSH (http://gmsh.info/) version 4.6 or
newer. Start GMSH and use ``File | Open`` menu or Crtl + O shortcut, navigate to
the output folder, select all ``.msh`` files and hit Open, all files should load
as one item in Post-processing named p_cell_nodes.

GMSH is capable of rendering high order approximations in individual elements,
to modify fidelity of rendering, double click the displayed mesh, quick options
menu should pop up, click on ``All view options...``. This brings up the Options
window with ``View [0]`` selected in left column. Under the tab ``General``
ensure that ``Adapt visualization grid`` is ticked, then you can adjust
``Maximum recursion depth`` and ```Target visualization error`` to tune
the visualization. To see visualization elements (as opposed to mesh elements)
go to ``Visibility`` tab and tick ``Draw element outlines``, this option is also
available from quick options menu as ``View element outlines`` or under shortcut
``Alt+E``. In the quick options menu, you can also modify normal raise by
clicking ``View Normal Raise`` to see solution rendered as surface above the
mesh. Note that for triangular meshes normal raise -1 produces expected raise
above the mesh. This is due to the opposite orientation of the reference
elements in GMSH and Sfepy and might get patched in the future.
"""

from sfepy.examples.dg.example_dg_common import *

def define(filename_mesh=None,
           approx_order=2,

          adflux=None,
           limit=False,

           cw=100,
           diffcoef=1,
           diffscheme="symmetric",

           cfl=None,
           dt=None,
           ):

    cfl = None
    dt = None

    functions = {}
    def local_register_function(fun):
        try:
            functions.update({fun.__name__: (fun,)})

        except AttributeError:  # Already a sfepy Function.
            fun = fun.function
            functions.update({fun.__name__: (fun,)})

        return fun

    example_name = "laplace_2D"
    dim = 2

    if filename_mesh is None:
        filename_mesh = get_gen_block_mesh_hook((1., 1.), (16, 16), (.5, .5))

    a = 1
    b = 1
    c = 0

    regions = {
        'Omega'     : 'all',
        'left' : ('vertices in x == 0', 'edge'),
        'right': ('vertices in x == 1', 'edge'),
        'top' : ('vertices in y == 1', 'edge'),
        'bottom': ('vertices in y == 0', 'edge')
    }
    fields = {
        'f': ('real', 'scalar', 'Omega', str(approx_order) + 'd', 'DG', 'legendre')  #
    }

    variables = {
        'p': ('unknown field', 'f', 0, 1),
        'v': ('test field', 'f', 'p'),
    }

    def analytic_sol(coors, t):
        x_1, x_2 = coors[..., 0], coors[..., 1]
        res = 1/2*x_1**2 - 1/2*x_2**2 - a*x_1 + b*x_2 + c
        return res


    @local_register_function
    def sol_fun(ts, coors, mode="qp", **kwargs):
        t = ts.time
        if mode == "qp":
            return {"p": analytic_sol(coors, t)[..., None, None]}

    @local_register_function
    def bc_funs(ts, coors, bc, problem):
        t = ts.time
        x_1, x_2 = coors[..., 0], coors[..., 1]
        res = nm.zeros(x_1.shape)
        if bc.diff == 0:
            res[:] = analytic_sol(coors, t)

        elif bc.diff == 1:
            res = nm.stack((x_1 - a, -x_2 + b),
                           axis=-2)
        return res

    materials = {
        'D'     : ({'val': [diffcoef], '.Cw': cw},),
    }

    dgebcs = {
        'u_left' : ('left', {'p.all': "bc_funs", 'grad.p.all': "bc_funs"}),
        'u_right' : ('right', {'p.all': "bc_funs", 'grad.p.all': "bc_funs"}),
        'u_bottom' : ('bottom', {'p.all': "bc_funs", 'grad.p.all': "bc_funs"}),
        'u_top' : ('top', {'p.all': "bc_funs", 'grad.p.all': "bc_funs"}),

    }

    integrals = {
        'i': 2 * approx_order,
    }

    equations = {
        'laplace': " dw_laplace.i.Omega(D.val, v, p) " +
                     diffusion_schemes_implicit[diffscheme] +
                     " + dw_dg_interior_penalty.i.Omega(D.val, D.Cw, v, p)" +
                     " = 0"
    }

    solver_0 = {
        'name' : 'ls',
        'kind' : 'ls.scipy_direct',
    }

    solver_1 = {
        'name' : 'newton',
        'kind' : 'nls.newton',

        # 'i_max'      : 5,
        # 'eps_a'      : 1e-8,
        # 'eps_r'      : 1.0,
        # 'macheps'   : 1e-16,
        # 'lin_red'    : 1e-2,  # Linear system error < (eps_a * lin_red).
        # 'ls_red'     : 0.1,
        # 'ls_red_warp' : 0.001,
        # 'ls_on'      : 0.99999,
        # 'ls_min'     : 1e-5,
        # 'check'     : 0,
        # 'delta'     : 1e-6,
    }

    options = {
        'nls'             : 'newton',
        'ls'              : 'ls',
        'output_dir'      : 'output/dg/' + example_name,
        'output_format'   : 'msh',
        'file_format'     : 'gmsh-dg',
        # 'pre_process_hook': get_cfl_setup(cfl)
    }
    return locals()