sfepy.terms.terms_adj_navier_stokes module¶

class sfepy.terms.terms_adj_navier_stokes.AdjConvect1Term(name, arg_str, integral, region, **kwargs)[source]¶

The first adjoint term to nonlinear convective term dw_convect.

Definition:

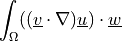
$\int_{\Omega} ((\ul{v} \cdot \nabla) \ul{u}) \cdot \ul{w}$

Call signature:

dw_adj_convect1

(virtual, state, parameter)

Arguments:

virtual : $\ul{v}$
state : $\ul{w}$
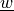
parameter : $\ul{u}$

arg_shapes = {'parameter': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶

arg_types = ('virtual', 'state', 'parameter')¶

static function(out, state_w, grad_u, cmap, is_diff)¶

get_fargs(virtual, state, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_adj_convect1'¶

class sfepy.terms.terms_adj_navier_stokes.AdjConvect2Term(name, arg_str, integral, region, **kwargs)[source]¶

The second adjoint term to nonlinear convective term dw_convect.

Definition:

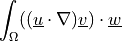
$\int_{\Omega} ((\ul{u} \cdot \nabla) \ul{v}) \cdot \ul{w}$

Call signature:

dw_adj_convect2

(virtual, state, parameter)

Arguments:

virtual : $\ul{v}$
state : $\ul{w}$
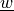
parameter : $\ul{u}$

arg_shapes = {'parameter': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶

arg_types = ('virtual', 'state', 'parameter')¶

static function(out, state_w, state_u, cmap, is_diff)¶

get_fargs(virtual, state, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_adj_convect2'¶

class sfepy.terms.terms_adj_navier_stokes.AdjDivGradTerm(name, arg_str, integral, region, **kwargs)[source]¶

Gateaux differential of 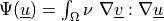$\Psi(\ul{u}) = \int_{\Omega} \nu\ \nabla \ul{v} : \nabla \ul{u}$ w.r.t. $\ul{u}$ in the direction $\ul{v}$ or adjoint term to dw_div_grad.

Definition:

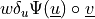
$w \delta_{u} \Psi(\ul{u}) \circ \ul{v}$

Call signature:

dw_adj_div_grad

(material_1, material_2, virtual, parameter)

Arguments:

material_1 : 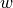$w$ (weight)
material_2 : 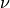$\nu$ (viscosity)
virtual : $\ul{v}$
state : $\ul{u}$

arg_shapes = {'material_1': '1, 1', 'material_2': '1, 1', 'parameter': 'D', 'virtual': ('D', None)}¶

arg_types = ('material_1', 'material_2', 'virtual', 'parameter')¶

static function(out, grad, viscosity, cmap_v, cmap_s, is_diff)¶

get_fargs(mat1, mat2, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_adj_div_grad'¶

class sfepy.terms.terms_adj_navier_stokes.NSOFMinGradTerm(name, arg_str, integral, region, **kwargs)[source]¶

Call signature:

d_of_ns_min_grad

(material_1, material_2, parameter)

arg_shapes = {'material_1': '1, 1', 'material_2': '1, 1', 'parameter': 1}¶

arg_types = ('material_1', 'material_2', 'parameter')¶

static function(out, grad, viscosity, cmap)¶

get_eval_shape(weight, mat, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(weight, mat, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'd_of_ns_min_grad'¶

class sfepy.terms.terms_adj_navier_stokes.NSOFSurfMinDPressDiffTerm(name, arg_str, integral, region, **kwargs)[source]¶

Gateaux differential of 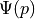$\Psi(p)$ w.r.t. $p$ in the direction $q$ .

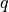Definition:

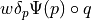
$w \delta_{p} \Psi(p) \circ q$

Call signature:

dw_of_ns_surf_min_d_press_diff

(material, virtual)

Arguments:

material : 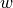$w$ (weight)
virtual : $q$

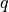
arg_shapes = {'material': 1, 'virtual': (1, None)}¶

arg_types = ('material', 'virtual')¶

get_fargs(weight, virtual, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_of_ns_surf_min_d_press_diff'¶

class sfepy.terms.terms_adj_navier_stokes.NSOFSurfMinDPressTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity of $\Psi(p)$ .

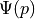Definition:

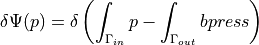
$\delta \Psi(p) = \delta \left( \int_{\Gamma_{in}}p - \int_{\Gamma_{out}}bpress \right)$

Call signature:

ev_of_ns_surf_min_d_press

(material_1, material_2, parameter)

Arguments:

material_1 : 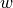$w$ (weight)
material_2 : 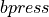$bpress$ (given pressure)
parameter : $p$

arg_shapes = {'material_1': 1, 'material_2': 1, 'parameter': 1}¶

arg_types = ('material_1', 'material_2', 'parameter')¶

static function(out, pressure, weight, bpress, cmap, is_diff)¶

get_eval_shape(weight, bpress, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(weight, bpress, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = 'facet'¶

name = 'ev_of_ns_surf_min_d_press'¶

class sfepy.terms.terms_adj_navier_stokes.SDConvectTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of convective term dw_convect.

Supports the following term modes: 1 (sensitivity) or 0 (original term value).

Definition:

$\int_{\Omega} [ u_k \pdiff{u_i}{x_k} w_i (\nabla \cdot \Vcal) - u_k \pdiff{\Vcal_j}{x_k} \pdiff{u_i}{x_j} w_i ]$

Call signature:

ev_sd_convect

(parameter_u, parameter_w, parameter_mv)

Arguments:

parameter_u : $\ul{u}$
parameter_w : $\ul{w}$
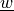
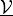
parameter_mv : $\ul{\Vcal}$

arg_shapes = {'parameter_mv': 'D', 'parameter_u': 'D', 'parameter_w': 'D'}¶

arg_types = ('parameter_u', 'parameter_w', 'parameter_mv')¶

static function(out, state_u, grad_u, state_w, div_mv, grad_mv, cmap_u, mode)¶

get_eval_shape(par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_convect'¶

class sfepy.terms.terms_adj_navier_stokes.SDDivGradTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of diffusion term dw_div_grad.

Supports the following term modes: 1 (sensitivity) or 0 (original term value).

Definition:

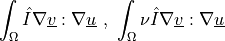
$\int_{\Omega} \hat{I} \nabla \ul{v} : \nabla \ul{u} \mbox{ , } \int_{\Omega} \nu \hat{I} \nabla \ul{v} : \nabla \ul{u}$

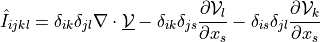
$\hat{I}_{ijkl} = \delta_{ik}\delta_{jl} \nabla \cdot \ul{\Vcal} - \delta_{ik}\delta_{js} {\partial \Vcal_l \over \partial x_s} - \delta_{is}\delta_{jl} {\partial \Vcal_k \over \partial x_s}$

Call signature:

ev_sd_div_grad

(opt_material, parameter_u, parameter_w, parameter_mv)

Arguments:

material : 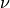$\nu$ (viscosity, optional)
parameter_u : $\ul{u}$
parameter_w : $\ul{w}$
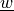
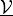
parameter_mv : $\ul{\Vcal}$

arg_shapes = [{'opt_material': '1, 1', 'parameter_mv': 'D', 'parameter_u': 'D', 'parameter_w': 'D'}, {'opt_material': None}]¶

arg_types = ('opt_material', 'parameter_u', 'parameter_w', 'parameter_mv')¶

static function(out, grad_u, grad_w, div_mv, grad_mv, viscosity, cmap_u, mode)¶

get_eval_shape(mat, par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(mat, par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_div_grad'¶

class sfepy.terms.terms_adj_navier_stokes.SDDivTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of Stokes term dw_stokes in ‘div’ mode.

Supports the following term modes: 1 (sensitivity) or 0 (original term value).

Definition:

$\int_{\Omega} p [ (\nabla \cdot \ul{w}) (\nabla \cdot \ul{\Vcal}) - \pdiff{\Vcal_k}{x_i} \pdiff{w_i}{x_k} ]$

Call signature:

ev_sd_div

(parameter_u, parameter_p, parameter_mv)

Arguments:

parameter_u : $\ul{u}$
parameter_p : $p$
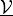
parameter_mv : $\ul{\Vcal}$

arg_shapes = {'parameter_mv': 'D', 'parameter_p': 1, 'parameter_u': 'D'}¶

arg_types = ('parameter_u', 'parameter_p', 'parameter_mv')¶

static function(out, div_u, grad_u, state_p, div_mv, grad_mv, cmap_u, mode)¶

get_eval_shape(par_u, par_p, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(par_u, par_p, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_div'¶

class sfepy.terms.terms_adj_navier_stokes.SDDotTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of dot product of scalars or vectors.

Definition:

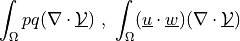
$\int_{\Omega} p q (\nabla \cdot \ul{\Vcal}) \mbox{ , } \int_{\Omega} (\ul{u} \cdot \ul{w}) (\nabla \cdot \ul{\Vcal})$

Call signature:

ev_sd_dot

(parameter_1, parameter_2, parameter_mv)

Arguments:

parameter_1 : $p$ or $\ul{u}$
parameter_2 : 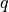$q$ or $\ul{w}$
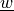
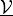
parameter_mv : $\ul{\Vcal}$

arg_shapes = [{'parameter_1': 'D', 'parameter_2': 'D', 'parameter_mv': 'D'}, {'parameter_1': 1, 'parameter_2': 1}]¶

arg_types = ('parameter_1', 'parameter_2', 'parameter_mv')¶

static function(out, state_p, state_q, div_mv, cmap, mode)¶

get_eval_shape(par1, par2, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(par1, par2, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_dot'¶

class sfepy.terms.terms_adj_navier_stokes.SDGradDivStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of stabilization term dw_st_grad_div.

Definition:

$\gamma \int_{\Omega} [ (\nabla \cdot \ul{u}) (\nabla \cdot \ul{w}) (\nabla \cdot \ul{\Vcal}) - \pdiff{u_i}{x_k} \pdiff{\Vcal_k}{x_i} (\nabla \cdot \ul{w}) - (\nabla \cdot \ul{u}) \pdiff{w_i}{x_k} \pdiff{\Vcal_k}{x_i} ]$

Call signature:

ev_sd_st_grad_div

(material, parameter_u, parameter_w, parameter_mv)

Arguments:

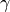
material : $\gamma$
parameter_u : $\ul{u}$
parameter_w : $\ul{w}$
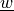
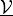
parameter_mv : $\ul{\Vcal}$
mode : 1 (sensitivity) or 0 (original term value)

arg_shapes = {'material': '1, 1', 'parameter_mv': 'D', 'parameter_u': 'D', 'parameter_w': 'D'}¶

arg_types = ('material', 'parameter_u', 'parameter_w', 'parameter_mv')¶

static function(out, div_u, grad_u, div_w, grad_w, div_mv, grad_mv, coef, cmap_u, mode)¶

get_eval_shape(mat, par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(mat, par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_st_grad_div'¶

class sfepy.terms.terms_adj_navier_stokes.SDPSPGCStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of stabilization terms dw_st_supg_p or dw_st_pspg_c.

Definition:

$\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ [ \pdiff{r}{x_i} (\ul{b} \cdot \nabla u_i) (\nabla \cdot \Vcal) - \pdiff{r}{x_k} \pdiff{\Vcal_k}{x_i} (\ul{b} \cdot \nabla u_i) - \pdiff{r}{x_k} (\ul{b} \cdot \nabla \Vcal_k) \pdiff{u_i}{x_k} ]$

Call signature:

ev_sd_st_pspg_c

(material, parameter_b, parameter_u, parameter_r, parameter_mv)

Arguments:

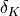
material : $\delta_K$
parameter_b : $\ul{b}$
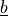
parameter_u : $\ul{u}$
parameter_r : $r$
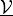
parameter_mv : $\ul{\Vcal}$
mode : 1 (sensitivity) or 0 (original term value)

arg_shapes = {'material': '1, 1', 'parameter_b': 'D', 'parameter_mv': 'D', 'parameter_r': 1, 'parameter_u': 'D'}¶

arg_types = ('material', 'parameter_b', 'parameter_u', 'parameter_r', 'parameter_mv')¶

static function(out, state_b, grad_u, grad_r, div_mv, grad_mv, coef, cmap_u, mode)¶

get_eval_shape(mat, par_b, par_u, par_r, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(mat, par_b, par_u, par_r, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_st_pspg_c'¶

class sfepy.terms.terms_adj_navier_stokes.SDPSPGPStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of stabilization term dw_st_pspg_p.

Definition:

$\sum_{K \in \Ical_h}\int_{T_K} \tau_K\ [ (\nabla r \cdot \nabla p) (\nabla \cdot \Vcal) - \pdiff{r}{x_k} (\nabla \Vcal_k \cdot \nabla p) - (\nabla r \cdot \nabla \Vcal_k) \pdiff{p}{x_k} ]$

Call signature:

ev_sd_st_pspg_p

(material, parameter_r, parameter_p, parameter_mv)

Arguments:

material : $\tau_K$
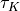
parameter_r : $r$
parameter_p : $p$
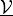
parameter_mv : $\ul{\Vcal}$
mode : 1 (sensitivity) or 0 (original term value)

arg_shapes = {'material': '1, 1', 'parameter_mv': 'D', 'parameter_p': 1, 'parameter_r': 1}¶

arg_types = ('material', 'parameter_r', 'parameter_p', 'parameter_mv')¶

static function(out, grad_r, grad_p, div_mv, grad_mv, coef, cmap_p, mode)¶

get_eval_shape(mat, par_r, par_p, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(mat, par_r, par_p, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_st_pspg_p'¶

class sfepy.terms.terms_adj_navier_stokes.SDSUPGCStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

Sensitivity (shape derivative) of stabilization term dw_st_supg_c.

Definition:

$\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ [ (\ul{b} \cdot \nabla u_k) (\ul{b} \cdot \nabla w_k) (\nabla \cdot \Vcal) - (\ul{b} \cdot \nabla \Vcal_i) \pdiff{u_k}{x_i} (\ul{b} \cdot \nabla w_k) - (\ul{u} \cdot \nabla u_k) (\ul{b} \cdot \nabla \Vcal_i) \pdiff{w_k}{x_i} ]$

Call signature:

ev_sd_st_supg_c

(material, parameter_b, parameter_u, parameter_w, parameter_mv)

Arguments:

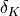
material : $\delta_K$
parameter_b : $\ul{b}$
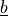
parameter_u : $\ul{u}$
parameter_w : $\ul{w}$
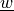
parameter_mv : $\ul{\Vcal}$
mode : 1 (sensitivity) or 0 (original term value)

arg_shapes = {'material': '1, 1', 'parameter_b': 'D', 'parameter_mv': 'D', 'parameter_u': 'D', 'parameter_w': 'D'}¶

arg_types = ('material', 'parameter_b', 'parameter_u', 'parameter_w', 'parameter_mv')¶

static function(out, state_b, grad_u, grad_w, div_mv, grad_mv, coef, cmap_u, mode)¶

get_eval_shape(mat, par_b, par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

get_fargs(mat, par_b, par_u, par_w, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'ev_sd_st_supg_c'¶

class sfepy.terms.terms_adj_navier_stokes.SUPGCAdjStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

Adjoint term to SUPG stabilization term dw_st_supg_c.

Definition:

$\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ [ ((\ul{v} \cdot \nabla) \ul{u}) ((\ul{u} \cdot \nabla) \ul{w}) + ((\ul{u} \cdot \nabla) \ul{u}) ((\ul{v} \cdot \nabla) \ul{w}) ]$

Call signature:

dw_st_adj_supg_c

(material, virtual, parameter, state)

Arguments:

material : $\delta_K$
virtual : $\ul{v}$
state : $\ul{w}$
parameter : $\ul{u}$

arg_shapes = {'material': '1, 1', 'parameter': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶

arg_types = ('material', 'virtual', 'parameter', 'state')¶

static function(out, state_w, state_u, grad_u, coef, cmap, conn, is_diff)¶

get_fargs(mat, virtual, state, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_st_adj_supg_c'¶

class sfepy.terms.terms_adj_navier_stokes.SUPGPAdj1StabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

The first adjoint term to SUPG stabilization term dw_st_supg_p.

Definition:

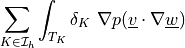
$\sum_{K \in \Ical_h}\int_{T_K} \delta_K\ \nabla p (\ul{v} \cdot \nabla \ul{w})$

Call signature:

dw_st_adj1_supg_p

(material, virtual, state, parameter)

Arguments:

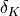
material : $\delta_K$
virtual : $\ul{v}$
state : $\ul{w}$
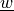
parameter : $p$

arg_shapes = {'material': '1, 1', 'parameter': 1, 'state': 'D', 'virtual': ('D', 'state')}¶

arg_types = ('material', 'virtual', 'state', 'parameter')¶

static function(out, state_w, grad_p, coef, cmap_w, conn_w, is_diff)¶

get_fargs(mat, virtual, state, parameter, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_st_adj1_supg_p'¶

class sfepy.terms.terms_adj_navier_stokes.SUPGPAdj2StabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶

The second adjoint term to SUPG stabilization term dw_st_supg_p as well as adjoint term to PSPG stabilization term dw_st_pspg_c.

Definition:

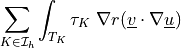
$\sum_{K \in \Ical_h}\int_{T_K} \tau_K\ \nabla r (\ul{v} \cdot \nabla \ul{u})$

Call signature:

dw_st_adj2_supg_p

(material, virtual, parameter, state)

Arguments:

material : $\tau_K$
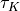
virtual : $\ul{v}$
parameter : $\ul{u}$
state : $r$

arg_shapes = {'material': '1, 1', 'parameter': 'D', 'state': 1, 'virtual': ('D', 'state')}¶

arg_types = ('material', 'virtual', 'parameter', 'state')¶

static function(out, grad_u, state_r, coef, cmap_u, cmap_r, conn_r, is_diff)¶

get_fargs(mat, virtual, parameter, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

name = 'dw_st_adj2_supg_p'¶

sfepy.terms.terms_adj_navier_stokes.grad_as_vector(grad)[source]¶