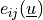Developer Guide¶
This section purports to document the SfePy internals. It is mainly useful for those who wish to contribute to the development of SfePy and understand the inner workings of the code.
We use git to track source code, documentation, examples, and other files related to the project.
It is not necessary to learn git in order to contribute to SfePy but we strongly suggest you do so as soon as possible - it is an extremely useful tool not just for writing code, but also for tracking revisions of articles, Ph.D. theses, books, … it will also look well in your CV :-) It is also much easier for us to integrate changes that are in form of a github pull request than in another form.
Retrieving the Latest Code¶
The first step is to obtain the latest development version of the code from the SfePy git repository:
git clone git://github.com/sfepy/sfepy.git
For development, it is preferable to build the extension modules in place (see Compilation of C Extension Modules):
python setup.py build_ext --inplace
On Unix-like systems, you can simply type make in the top-level folder to
build in-place.
After the initial compilation, or after making changes, do not forget to run the tests, see Testing Installation.
SfePy Directory Structure¶
Here we list and describe the directories that are in the main sfepy directory.
name |
description |
|---|---|
build/ |
directory created by the build process (generated) |
doc/ |
source files of this documentation |
meshes/ |
finite element mesh files in various formats shared by the examples |
output/ |
default output directory for storing results of the examples |
sfepy/ |
the source code including examples and tests |
tools/ |
various helper scripts (build, documentation generation etc.) |
New users/developers (after going through the Tutorial) should explore the sfepy/examples/ directory. For developers, the principal directory is sfepy/, which has the following contents:
name |
description |
field-specific |
|---|---|---|
applications/ |
top level application classes (e.g. |
|
base/ |
common utilities and classes used by most of the other modules |
|
discrete/ |
general classes and modules for describing a discrete problem, taking care of boundary conditions, degrees of freedom, approximations, variables, equations, meshes, regions, quadratures, etc. Discretization-specific classes are in subdirectories:
|
|
examples/ |
the examples using both the declarative and imperative problem description API |
|
homogenization/ |
the homogenization engine and supporting modules - highly specialized code, one of the reasons of SfePy existence |
|
linalg/ |
linear algebra functions not covered by NumPy and SciPy |
|
mechanics/ |
modules for (continuum) mechanics: elastic constant conversions, tensor, units utilities, etc. |
|
mesh/ |
some utilities to interface with tetgen and triangle mesh generators |
|
parallel/ |
modules supporting parallel assembling and solution of problems |
|
postprocess/ |
Matplotlib and VTK based post-processing modules |
|
scripts/ |
the main as well as auxiliary scripts |
|
solvers/ |
interface classes to various internal/external solvers (linear, nonlinear, eigenvalue, optimization, time stepping) |
|
terms/ |
implementation of the terms (weak formulation integrals), see Term Overview |
|
tests/ |
the tests |
The directories in the “field-specific” column are mostly interesting for specialists working in the respective fields.
The discrete/ is the heart of the code, while the terms/ contains the particular integral forms usable to build equations - new term writers should look there.
Exploring the Code¶
It is convenient to install IPython to have the tab completion available. Moreover, all SfePy classes can be easily examined by printing them:
1In [1]: from sfepy.discrete.fem import Mesh
2
3In [2]: mesh = Mesh.from_file('meshes/2d/rectangle_tri.mesh')
4sfepy: reading mesh [line2, tri3, quad4, tetra4, hexa8] (meshes/2d/rectangle_tri.mesh)...
5sfepy: ...done in 0.00 s
6
7In [3]: print(mesh)
8Mesh:meshes/2d/rectangle_tri
9 cmesh:
10 CMesh: n_coor: 258, dim 2, tdim: 2, n_el 454
11 descs:
12 list: ['2_3']
13 dim:
14 2
15 dims:
16 list: [2]
17 io:
18 None
19 n_el:
20 454
21 n_nod:
22 258
23 name:
24 meshes/2d/rectangle_tri
25 nodal_bcs:
26 dict with keys: []
We recommend going through the interactive example in the tutorial Interactive Example: Linear Elasticity in this way, printing all the variables.
Another useful tool is the debug() function,
that can be used as follows:
from sfepy.base.base import debug; debug()
Try to use it in the examples with user defined functions to explore their parameters etc. It works best with IPython installed, as then the tab completion is available also when debugging.
How to Contribute¶
Read this section if you wish to contribute some work to the SfePy project - everyone is welcome to contribute. Contributions can be made in a variety of forms, not just code. Reporting bugs and contributing to the documentation, tutorials, and examples is in great need!
Below we describe
where to report problems or find existing issues and additional development suggestions
what to do to apply changes/fixes
what to do after you made your changes/fixes
Reporting problems¶
Reporting a bug is the first way in which to contribute to an open source project
Short version: go to the main SfePy site and follow the links given there.
When you encounter a problem, try searching that site first - an answer may already be posted in the SfePy mailing list (to which we suggest you subscribe…), or the problem might have been added to the SfePy issues. As is true in any open source project, doing your homework by searching for existing known problems greatly reduces the burden on the developers by eliminating duplicate issues. If you find your problem already exists in the issue tracker, feel free to gather more information and append it to the issue. In case the problem is not there, create a new issue with proper labels for the issue type and priority, and/or ask us using the mailing list.
Note: A google account (e.g., gmail account) is needed to join the mailing list. A github account is needed for working with the source code repository and issues.
Note: When reporting a problem, try to provide as much information as possible concerning the version of SfePy, the OS / Linux distribution, and the versions of Python, NumPy and SciPy, and other prerequisites. The versions found on your system can be printed by running:
python setup.py --help
If you are a new user, please let us know what difficulties you have with this documentation. We greatly welcome a variety of contributions not limited to code only.
Contributing changes¶
Note: To avoid duplicating work, it is highly advised that you contact the developers on the mailing list or create an enhancement issue before starting work on a non-trivial feature.
Before making any changes, read the Notes on commits and patches.
Using git and github¶
The preferred way to contribute to SfePy is to fork the main repository on github, then submit a “pull request” (PR):
Create a github account if you do not already have one.
Fork the project repository: click on the “Fork” button near the top of the sfepy git repository page. This creates a copy of the repository under your account on the github server.
Clone your fork to your computer:
git clone git@github.com:YourLogin/sfepy.git
If you have never used git before, introduce yourself to git and make (optionally) some handy aliases either in
.gitconfigin your home directory (global settings for all your git projects), or directly in.git/configin the repository:1[user] 2 email = mail@mail.org 3 name = Name Surname 4 5[color] 6 ui = auto 7 interactive = true 8 9[alias] 10 ci = commit 11 di = diff --color-words 12 st = status 13 co = checkout
Create a feature branch to hold your changes:
git checkout -b my-feature
Then you can start to make your changes. Do not work in the master branch!
Modify some files and use git to track your local changes. The changed added/modified files can be listed using:
git status
and the changes can be reviewed using:
git diff
A more convenient way of achieving the above is to run:
gitk --all
in order to visualize of project history (all branches). There are other GUIs for this purpose, e.g.
qgit. You may need to install those tools, as they usually are not installed with git by default. Record a set of changes by:1# schedule some of the changed files for the next commit 2git add file1 file2 ... 3# an editor will pop up where you should describe the commit 4git commit
We recommend
git guicommand in case you want to add and commit only some changes in a modified file.Note: Do not be afraid to experiment - git works with your local copy of the repository, so it is not possible to damage the master repository. It is always possible to re-clone a fresh copy, in case you do something that is really bad.
The commit(s) now reflect changes, but only in your local git repository. To update your github repository with your new commit(s), run:
git push origin my-feature:my-feature
Finally, when your feature is ready, and all tests pass, go to the github page of your sfepy repository fork, and click “Pull request” to send your changes to the maintainers for review. Continuous integration (CI) will run and check that the changes pass tests on Windows, Linux and Mac using Github Actions. The results will be displayed in the Pull Request discussion. The CI setup is located in the file .github/workflows/build_and_test_matrix.yml. It is recommended to check that your contribution complies with the Notes on commits and patches.
In the above setup, your origin remote repository points to
YourLogin/sfepy.git. If you wish to fetch/merge from the main repository
instead of your forked one, you will need to add another remote to use instead
of origin. The main repository is usually called “upstream”. To add it, type:
git remote add upstream https://github.com/sfepy/sfepy.git
To synchronize your repository with the upstream, proceed as follows:
Fetch the upstream changes:
git fetch upstream
Never start with
git pull upstream!Check the changes of the upstream master branch. You can use
gitk --allto visualize all your and remote branches. The upstream master is namedremotes/upstream/master.Make sure all your local changes are either committed in a feature branch or stashed (see
git stash). Then reset your master to the upstream master:git checkout master git reset --hard upstream/master
Warning The above will remove all your local commits in the master branch that are not in
upstream/master, and also reset all the changes in your non-committed modified files!Optionally, the reset command can be run conveniently in
gitkby right-clicking on a commit you want to reset the current branch onto.Optionally, rebase your feature branch onto the upstream master:
git checkout my-feature git rebase upstream/master
This is useful, for example, when the upstream master contains a change you need in your feature branch.
For additional information, see, for example, the gitwash git tutorial, or its incarnation NumPy gitwash.
Notes on commits and patches¶
Follow our Coding style.
Do not use lines longer than 79 characters (exception: tables of values, e.g., quadratures).
Write descriptive docstrings in correct style, see Docstring standard.
There should be one patch for one topic - do not mix unrelated things in one patch. For example, when you add a new function, then notice a typo in docstring in a nearby function and correct it, create two patches: one fixing the docstring, the other adding the new function.
The commit message and description should clearly state what the patch does. Try to follow the style of other commit messages. Some interesting notes can be found at tbaggery.com, namely that the commit message is better to be written in the present tense: “fix bug” and not “fixed bug”.
Without using git¶
Without using git, send the modified files to the SfePy mailing list or attach them using gist to the corresponding issue at the Issues web page. Do not forget to describe the changes properly, and to follow the spirit of Notes on commits and patches and the Coding style.
Coding style¶
All the code in SfePy should try to adhere to python style guidelines, see PEP-0008.
There are some additional recommendations:
Prefer whole words to abbreviations in public APIs - there is completion after all. If some abbreviation is needed (really too long name), try to make it as comprehensible as possible. Also check the code for similar names - try to name things consistently with the existing code. Examples:
yes:
equation,transform_variables(),filenamerather not:
eq,transvar(),fname
Functions have usually form
<action>_<subject>()e.g.:save_data(),transform_variables(), do not usedata_save(),variable_transform()etc.Variables like
V,c,A,b,xshould be tolerated only locally when expressing mathematical ideas.
Really minor recommendations:
Avoid single letter names, if you can:
not even for loop variables - use e.g. ir, ic, … instead of i, j for rows and columns
not even in generators, as they “leak” (this is fixed in Python 3.x)
These are recommendations only, we will not refuse code just on the ground that it uses slightly different formatting, as long as it follows the PEP.
Note: some old parts of the code might not follow the PEP, yet. We fix them progressively as we update the code.
Docstring standard¶
We use sphinx with the numpydoc extension to generate this documentation. Refer to the sphinx site for the possible markup constructs.
Basically (with a little tweak), we try to follow the NumPy/SciPy docstring standard as described in NumPy documentation guide. See also the complete docstring example. It is exaggerated a bit to show all the possibilities. Use your common sense here - the docstring should be sufficient for a new user to use the documented object. A good way to remember the format is to type:
In [1]: import numpy as nm
In [2]: nm.sin?
in ipython. The little tweak mentioned above is the starting newline:
1def function(arg1, arg2):
2 """
3 This is a function.
4
5 Parameters
6 ----------
7 arg1 : array
8 The coordinates of ...
9 arg2 : int
10 The dimension ...
11
12 Returns
13 -------
14 out : array
15 The resulting array of shape ....
16 """
It seems visually better than:
1def function(arg1, arg2):
2 """This is a function.
3
4 Parameters
5 ----------
6 arg1 : array
7 The coordinates of ...
8 arg2 : int
9 The dimension ...
10
11 Returns
12 -------
13 out : array
14 The resulting array of shape ....
15 """
When using  in a docstring, use a raw string:
in a docstring, use a raw string:
1def function():
2 r"""
3 This is a function with :math:`\mbox{\LaTeX}` math:
4 :math:`\frac{1}{\pi}`.
5 """
to prevent Python from interpreting and consuming the backslashes in common escape sequences like ‘\n’, ‘\f’ etc.
How to Regenerate Documentation¶
The following steps summarize how to regenerate this documentation.
Install sphinx, numpydoc, `sphinx-rtd-theme`_ and IPython. Do not forget to set the path to numpydoc in site_cfg.py if it is not installed in a standard location for Python packages on your platform. A recent
 distribution is
required, too, for example TeX Live. Depending on your OS/platform, it
can be in the form of one or several packages.
distribution is
required, too, for example TeX Live. Depending on your OS/platform, it
can be in the form of one or several packages.Edit the rst files in doc/ directory using your favorite text editor - the ReST format is really simple, so nothing fancy is needed. Follow the existing files in doc/; for reference also check reStructuredText Primer, Sphinx Markup Constructs and docutils reStructuredText.
When adding a new Python module, add a corresponding documentation file into doc/src/sfepy/<path>, where <path> should reflect the location of the module in sfepy/.
Figures belong to doc/images; subdirectories can be used.
(Re)generate the documentation (assuming GNU make is installed):
cd doc make html
View it (substitute your favorite browser):
firefox _build/html/index.html
How to Implement a New Term¶
Warning Implementing a new term usually involves C. As Cython is now supported by our build system, it should not be that difficult. Python-only terms are possible as well.
Note There is an experimental way (newly from version 2021.1) of implementing multi-linear terms that is much easier than what is described here, see Multi-linear Terms.
Notes on terminology¶
Term integrals are over domains of the cell or facet kinds. For meshes with
elements of the topological dimension 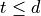 , where
, where 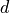 is the
space dimension, cells have the topological
is the
space dimension, cells have the topological 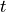 , while facets
, while facets
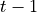 . For example, in 3D meshes cell = volume, facet = surface, while in
2D cell = area, facet = curve.
. For example, in 3D meshes cell = volume, facet = surface, while in
2D cell = area, facet = curve.
Introduction¶
A term in SfePy usually corresponds to a single integral term in (weak) integral formulation of an equation. Both cell and facet integrals are supported. There are three types of arguments a term can have:
variables, i.e. the unknown, test or parameter variables declared by the variables keyword, see sec-problem-description-file,
materials, corresponding to material and other parameters (functions) that are known, declared by the materials keyword,
user data - anything, but user is responsible for passing them to the evaluation functions.
SfePy terms are subclasses of sfepy.terms.terms.Term. The purpose of a
term is to implement a (vectorized) function that evaluates the term
contribution to residual/matrix and/or evaluates the term integral in elements
of the term region. Many such functions are currently implemented in C, but
some terms are pure Python, vectorized using NumPy.
Evaluation modes¶
A term can support several evaluation modes, as described in Term Evaluation.
Basic attributes¶
A term class should inherit from sfepy.terms.terms.Term base
class. The simplest possible term with cell integration and ‘weak’
evaluation mode needs to have the following attributes and methods:
docstring (not really required per se, but we require it);
name attribute - the name to be used in equations;
arg_types attribute - the types of arguments the term accepts;
integration attribute, optional - the kind of integral the term implements, one of ‘cell’ (the default, if not given), ‘facet’ or ‘facet_extra’;
function() static method - the assembling function;
get_fargs() method - the method that takes term arguments and converts them to arguments for function().
Argument types¶
The argument types can be (“[_*]” denotes an optional suffix):
‘material[_*]’ for a material parameter, i.e. any function that can be can evaluated in quadrature points and that is not a variable;
‘opt_material[_*]’ for an optional material parameter, that can be left out - there can be only one in a term and it must be the first argument;
‘virtual’ for a virtual (test) variable (no value defined), ‘weak’ evaluation mode;
‘state[_*]’ for state (unknown) variables (have value), ‘weak’ evaluation mode;
‘parameter[_*]’ for parameter variables (have known value), any evaluation mode.
Only one ‘virtual’ variable is allowed in a term.
Integration kinds¶
The integration kinds have the following meaning:
‘cell’ for cell integral over a region that contains elements; uses cell connectivity for assembling;
‘facet’ for facet integral over a region that contains faces; uses facet connectivity for assembling;
‘facet_extra’ for facet integral over a region that contains faces; uses cell connectivity for assembling - this is needed if full gradients of a variable are required on the boundary.
function()¶
The function() static method has always the following arguments:
out, *args
where out is the already preallocated output array (change it in place!) and *args are any other arguments the function requires. These function arguments have to be provided by the get_fargs() method. The function returns zero status on success, nonzero on failure.
The out array has shape (n_el, 1, n_row, n_col), where n_el is the number of elements and n_row, n_col are matrix dimensions of the value on a single element.
get_fargs()¶
The get_fargs() method has always the same structure of arguments:
positional arguments corresponding to arg_types attribute:
example for a typical weak term:
for:
arg_types = ('material', 'virtual', 'state')
the positional arguments are:
material, virtual, state
keyword arguments common to all terms:
mode=None, term_mode=None, diff_var=None, **kwargs
here:
mode is the actual evaluation mode, default is ‘eval’;
term_mode is an optional term sub-mode influencing what the term should return (example: dw_tl_he_neohook term has ‘strain’ and ‘stress’ evaluation sub-modes);
diff_var is taken into account in the ‘weak’ evaluation mode. It is either None (residual mode) or a name of variable with respect to differentiate to (matrix mode);
**kwargs are any other arguments that the term supports.
The get_fargs() method returns arguments for function().
Additional attributes¶
These attributes are used mostly in connection with the tests/test_term_call_modes.py test for automatic testing of term calls.
arg_shapes attribute - the possible shapes of term arguments;
geometries attribute - the list of reference element geometries that the term supports;
mode attribute - the default evaluation mode.
Argument shapes¶
The argument shapes are specified using a dict of the following form:
arg_shapes = {'material' : 'D, D', 'virtual' : (1, 'state'),
'state' : 1, 'parameter_1' : 1, 'parameter_2' : 1}
The keys are the argument types listed in the arg_types attribute, for example:
arg_types = (('material', 'virtual', 'state'),
('material', 'parameter_1', 'parameter_2'))
The values are the shapes containing either integers, or ‘D’ (for space dimension) or ‘S’ (symmetric storage size corresponding to the space dimension). For materials, the shape is a string ‘nr, nc’ or a single value, denoting a special-valued term, or None denoting an optional material that is left out. For state and parameter variables, the shape is a single value. For virtual variables, the shape is a tuple of a single shape value and a name of the corresponding state variable; the name can be None.
When several alternatives are possible, a list of dicts can be used. For convenience, only the shapes of arguments that change w.r.t. a previous dict need to be included, as the values of the other shapes are taken from the previous dict. For example, the following corresponds to a case, where an optional material has either the shape (1, 1) in each point, or is left out:
1arg_types = ('opt_material', 'parameter')
2arg_shapes = [{'opt_material' : '1, 1', 'parameter' : 1},
3 {'opt_material' : None}]
Geometries¶
The default that most terms use is a list of all the geometries:
geometries = ['2_3', '2_4', '3_4', '3_8']
In that case, the attribute needs not to be define explicitly.
Examples¶
Let us now discuss the implementation of a simple weak term
dw_integrate defined as 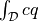 , where
, where  is a
weight (material parameter) and
is a
weight (material parameter) and 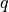 is a virtual variable. This term is
implemented as follows:
is a virtual variable. This term is
implemented as follows:
1class IntegrateOperatorTerm(Term):
2 r"""
3 Integral of a test function weighted by a scalar function
4 :math:`c`.
5
6 :Definition:
7
8 .. math::
9 \int_{\cal{D}} q \mbox{ or } \int_{\cal{D}} c q
10
11 :Arguments:
12 - material : :math:`c` (optional)
13 - virtual : :math:`q`
14 """
15 name = 'dw_integrate'
16 arg_types = ('opt_material', 'virtual')
17 arg_shapes = [{'opt_material' : '1, 1', 'virtual' : (1, None)},
18 {'opt_material' : None}]
19 integration = ('cell', 'facet')
20
21 @staticmethod
22 def function(out, material, bf, geo):
23 bf_t = nm.tile(bf.transpose((0, 1, 3, 2)), (out.shape[0], 1, 1, 1))
24 bf_t = nm.ascontiguousarray(bf_t)
25 if material is not None:
26 status = geo.integrate(out, material * bf_t)
27 else:
28 status = geo.integrate(out, bf_t)
29 return status
30
31 def get_fargs(self, material, virtual,
32 mode=None, term_mode=None, diff_var=None, **kwargs):
33 assert_(virtual.n_components == 1)
34 geo, _ = self.get_mapping(virtual)
35
36 return material, geo.bf, geo
lines 2-14: the docstring - always write one!
line 15: the name of the term, that can be referred to in equations;
line 16: the argument types - here the term takes a single material parameter, and a virtual variable;
lines 17-18: the possible argument shapes
line 19: the integration mode is choosen according to a given domain
lines 21-29: the term function
its arguments are:
the output array out, already having the required shape,
the material coefficient (array) mat evaluated in physical quadrature points of elements of the term region,
a base function (array) bf evaluated in the quadrature points of a reference element and
a reference element (geometry) mapping geo.
line 23: transpose the base function and tile it so that is has the correct shape - it is repeated for each element;
line 24: ensure C contiguous order;
lines 25-28: perform numerical integration in C - geo.integrate() requires the C contiguous order;
line 29: return the status.
lines 31-36: prepare arguments for the function above:
line 33: verify that the variable is scalar, as our implementation does not support vectors;
line 34: get reference element mapping corresponding to the virtual variable;
line 36: return the arguments for the function.
A more complex term that involves an unknown variable and has two call modes,
is dw_s_dot_mgrad_s, defined as 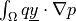 in the`’grad_state’` mode or
in the`’grad_state’` mode or 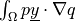 in
the ‘grad_virtual’ mode, where
in
the ‘grad_virtual’ mode, where 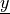 is a vector material parameter,
is a vector material parameter,
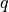 is a virtual variable, and
is a virtual variable, and 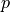 is a state variable:
is a state variable:
1class ScalarDotMGradScalarTerm(Term):
2 r"""
3 Volume dot product of a scalar gradient dotted with a material vector
4 with a scalar.
5
6 :Definition:
7
8 .. math::
9 \int_{\Omega} q \ul{y} \cdot \nabla p \mbox{ , }
10 \int_{\Omega} p \ul{y} \cdot \nabla q
11
12 :Arguments 1:
13 - material : :math:`\ul{y}`
14 - virtual : :math:`q`
15 - state : :math:`p`
16
17 :Arguments 2:
18 - material : :math:`\ul{y}`
19 - state : :math:`p`
20 - virtual : :math:`q`
21 """
22 name = 'dw_s_dot_mgrad_s'
23 arg_types = (('material', 'virtual', 'state'),
24 ('material', 'state', 'virtual'))
25 arg_shapes = [{'material' : 'D, 1',
26 'virtual/grad_state' : (1, None),
27 'state/grad_state' : 1,
28 'virtual/grad_virtual' : (1, None),
29 'state/grad_virtual' : 1}]
30 modes = ('grad_state', 'grad_virtual')
31
32 @staticmethod
33 def function(out, out_qp, geo, fmode):
34 status = geo.integrate(out, out_qp)
35 return status
36
37 def get_fargs(self, mat, var1, var2,
38 mode=None, term_mode=None, diff_var=None, **kwargs):
39 vg1, _ = self.get_mapping(var1)
40 vg2, _ = self.get_mapping(var2)
41
42 if diff_var is None:
43 if self.mode == 'grad_state':
44 geo = vg1
45 bf_t = vg1.bf.transpose((0, 1, 3, 2))
46 val_qp = self.get(var2, 'grad')
47 out_qp = bf_t * dot_sequences(mat, val_qp, 'ATB')
48
49 else:
50 geo = vg2
51 val_qp = self.get(var1, 'val')
52 out_qp = dot_sequences(vg2.bfg, mat, 'ATB') * val_qp
53
54 fmode = 0
55
56 else:
57 if self.mode == 'grad_state':
58 geo = vg1
59 bf_t = vg1.bf.transpose((0, 1, 3, 2))
60 out_qp = bf_t * dot_sequences(mat, vg2.bfg, 'ATB')
61
62 else:
63 geo = vg2
64 out_qp = dot_sequences(vg2.bfg, mat, 'ATB') * vg1.bf
65
66 fmode = 1
67
68 return out_qp, geo, fmode
Only interesting differences with respect to the previous example will by discussed:
the argument types and shapes (lines 23-29) have to be specified for all the call modes (line 30)
the term function (lines 32-35) just integrates the element contributions, as all the other calculations are done by the get_fargs() function.
the get_fargs() function (lines 37-68) contains:
residual computation (lines 43-54) for both modes
matrix computation (lines 57-66) for both modes
Concluding remarks¶
This is just a very basic introduction to the topic of new term implementation. Do not hesitate to ask the SfePy mailing list, and look at the source code of the already implemented terms.
Multi-linear Terms¶
tentative documentation, the enriched einsum notation is still in flux
Multi-linear terms can be implemented simply by using the following enriched einsum notation:
symbol |
meaning |
example |
|---|---|---|
|
scalar |
|
|
|
|
|
gradient: derivative of |
|
|
symmetric gradient |
|
|
vector storage of symmetric second order tensor, |
Cauchy strain tensor |
The examples below present the new way of implementing the terms shown in
the original Examples, using
sfepy.terms.terms_multilinear.ETermBase.
Examples¶
de_integrate defined as
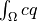 , where
, where  is
a weight (material parameter) and
is
a weight (material parameter) and 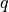 is a virtual variable:
is a virtual variable:1class EIntegrateOperatorTerm(ETermBase): 2 r""" 3 Volume and surface integral of a test function weighted by a scalar 4 function :math:`c`. 5 6 :Definition: 7 8 .. math:: 9 \int_{\cal{D}} q \mbox{ or } \int_{\cal{D}} c q 10 11 :Arguments: 12 - material : :math:`c` (optional) 13 - virtual : :math:`q` 14 """ 15 name = 'de_integrate' 16 arg_types = ('opt_material', 'virtual') 17 arg_shapes = [{'opt_material' : '1, 1', 'virtual' : (1, None)}, 18 {'opt_material' : None}] 19 20 def get_function(self, mat, virtual, mode=None, term_mode=None, 21 diff_var=None, **kwargs): 22 if mat is None: 23 fun = self.make_function( 24 '0', virtual, diff_var=diff_var, 25 ) 26 27 else: 28 fun = self.make_function( 29 '00,0', mat, virtual, diff_var=diff_var, 30 ) 31 32 return fun
de_s_dot_mgrad_s defined as
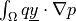 in the`’grad_state’` mode or
in the`’grad_state’` mode or 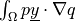 in
the ‘grad_virtual’ mode, where
in
the ‘grad_virtual’ mode, where 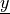 is a vector material
parameter,
is a vector material
parameter, 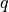 is a virtual variable, and
is a virtual variable, and 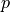 is a state
variable:
is a state
variable:1class EScalarDotMGradScalarTerm(ETermBase): 2 r""" 3 Volume dot product of a scalar gradient dotted with a material vector with 4 a scalar. 5 6 :Definition: 7 8 .. math:: 9 \int_{\Omega} q \ul{y} \cdot \nabla p \mbox{ , } 10 \int_{\Omega} p \ul{y} \cdot \nabla q 11 12 :Arguments 1: 13 - material : :math:`\ul{y}` 14 - virtual : :math:`q` 15 - state : :math:`p` 16 17 :Arguments 2: 18 - material : :math:`\ul{y}` 19 - state : :math:`p` 20 - virtual : :math:`q` 21 """ 22 name = 'de_s_dot_mgrad_s' 23 arg_types = (('material', 'virtual', 'state'), 24 ('material', 'state', 'virtual')) 25 arg_shapes = [{'material' : 'D, 1', 26 'virtual/grad_state' : (1, None), 27 'state/grad_state' : 1, 28 'virtual/grad_virtual' : (1, None), 29 'state/grad_virtual' : 1}] 30 modes = ('grad_state', 'grad_virtual') 31 32 def get_function(self, mat, var1, var2, mode=None, term_mode=None, 33 diff_var=None, **kwargs): 34 return self.make_function( 35 'i0,0,0.i', mat, var1, var2, diff_var=diff_var, 36 )
How To Make a Release¶
Module Index¶
sfepy package¶
sfepy.applications package¶
sfepy.base package¶
- sfepy.base.base module
debug()ContainerIndexedStructOneTypeListOutputStructas_float_or_complex()assert_()check_names()configure_output()debug()debug_on_error()dict_extend()dict_from_keys_init()dict_to_array()dict_to_struct()edit_dict_strings()edit_tuple_strings()find_subclasses()get_arguments()get_debug()get_default()get_default_attr()get_subdict()import_file()insert_as_static_method()insert_method()insert_static_method()invert_dict()ipython_shell()is_derived_class()is_integer()is_sequence()is_string()iter_dict_of_lists()load_classes()ordered_iteritems()pause()print_structs()python_shell()remap_dict()select_by_names()set_defaults()shell()spause()structify()try_imports()update_dict_recursively()use_method_with_name()
- sfepy.base.compat module
- sfepy.base.conf module
- Notes
ProblemConfdict_from_options()dict_from_string()get_standard_keywords()transform_conditions()transform_dgebcs()transform_dgepbcs()transform_ebcs()transform_epbcs()transform_fields()transform_functions()transform_ics()transform_integrals()transform_lcbcs()transform_materials()transform_regions()transform_solvers()transform_to_i_struct_1()transform_to_struct_01()transform_to_struct_1()transform_to_struct_10()transform_variables()tuple_to_conf()
- sfepy.base.getch module
- sfepy.base.goptions module
- sfepy.base.ioutils module
CachedDataMarkerDataSoftLinkHDF5BaseDataHDF5ContextManagerHDF5DataInDirSoftLinkUncacheddec()edit_filename()enc()ensure_path()get_or_create_hdf5_group()get_print_info()get_trunk()locate_files()look_ahead_line()path_of_hdf5_group()read_array()read_dict_hdf5()read_from_hdf5()read_list()read_sparse_matrix_from_hdf5()read_sparse_matrix_hdf5()read_token()remove_files()remove_files_patterns()save_options()skip_read_line()write_dict_hdf5()write_sparse_matrix_hdf5()write_sparse_matrix_to_hdf5()write_to_hdf5()
- sfepy.base.log module
- sfepy.base.log_plotter module
- sfepy.base.mem_usage module
- sfepy.base.multiproc module
- sfepy.base.multiproc_mpi module
MPIFileHandlerMPILogFileRemoteDictRemoteDictMasterRemoteIntRemoteLockRemoteQueueRemoteQueueMastercpu_count()enum()get_dict()get_int_value()get_logger()get_queue()get_slaves()is_remote_dict()master_loop()master_send_continue()master_send_task()set_logging_level()slave_get_task()slave_task_done()tagswait_for_tag()
- sfepy.base.multiproc_proc module
- sfepy.base.parse_conf module
- sfepy.base.plotutils module
- sfepy.base.reader module
- sfepy.base.resolve_deps module
- sfepy.base.testing module
- sfepy.base.timing module
sfepy.discrete package¶
This package implements various PDE discretization schemes (FEM or IGA).
- sfepy.discrete.conditions module
- sfepy.discrete.equations module
- sfepy.discrete.evaluate module
- sfepy.discrete.evaluate_variable module
- sfepy.discrete.functions module
- sfepy.discrete.integrals module
- sfepy.discrete.materials module
- sfepy.discrete.parse_equations module
- sfepy.discrete.parse_regions module
- sfepy.discrete.probes module
- sfepy.discrete.problem module
- sfepy.discrete.projections module
- sfepy.discrete.quadratures module
- sfepy.discrete.simplex_cubature module
- sfepy.discrete.variables module
sfepy.discrete.common sub-package¶
Common lower-level code and parent classes for FEM and IGA.
- sfepy.discrete.common.dof_info module
- sfepy.discrete.common.domain module
- sfepy.discrete.common.extmods._fmfield module
- sfepy.discrete.common.extmods._geommech module
- sfepy.discrete.common.extmods.assemble module
- sfepy.discrete.common.extmods.cmapping module
- sfepy.discrete.common.extmods.cmesh module
- sfepy.discrete.common.extmods.crefcoors module
- sfepy.discrete.common.fields module
- sfepy.discrete.common.global_interp module
- sfepy.discrete.common.mappings module
- sfepy.discrete.common.poly_spaces module
- sfepy.discrete.common.region module
sfepy.discrete.fem sub-package¶
- sfepy.discrete.fem.domain module
- sfepy.discrete.fem.extmods.bases module
- sfepy.discrete.fem.extmods.lobatto_bases module
- sfepy.discrete.fem.facets module
- sfepy.discrete.fem.fe_surface module
- sfepy.discrete.fem.fields_base module
- sfepy.discrete.fem.fields_hierarchic module
- sfepy.discrete.fem.fields_l2 module
- sfepy.discrete.fem.fields_nodal module
- sfepy.discrete.fem.fields_positive module
- sfepy.discrete.fem.geometry_element module
- sfepy.discrete.fem.history module
- sfepy.discrete.fem.lcbc_operators module
- sfepy.discrete.fem.linearizer module
- sfepy.discrete.fem.mappings module
- sfepy.discrete.fem.mesh module
- sfepy.discrete.fem.meshio module
- sfepy.discrete.fem.periodic module
- sfepy.discrete.fem.poly_spaces module
BernsteinSimplexPolySpaceBernsteinTensorProductPolySpaceFEPolySpaceLagrangeNodesLagrangePolySpaceLagrangeSimplexBPolySpaceLagrangeSimplexPolySpaceLagrangeTensorProductPolySpaceLagrangeWedgePolySpaceLobattoTensorProductPolySpaceNodeDescriptionSEMTensorProductPolySpaceSerendipityTensorProductPolySpaceeval_lagrange1d_basis()get_lgl_nodes()
- sfepy.discrete.fem.refine module
- sfepy.discrete.fem.refine_hanging module
- sfepy.discrete.fem._serendipity module
- sfepy.discrete.fem.utils module
sfepy.discrete.dg sub-package¶
sfepy.discrete.iga sub-package¶
- sfepy.discrete.iga.domain module
- sfepy.discrete.iga.domain_generators module
- sfepy.discrete.iga.extmods.igac module
- sfepy.discrete.iga.fields module
- sfepy.discrete.iga.iga module
- Notes
combine_bezier_extraction()compute_bezier_control()compute_bezier_extraction()compute_bezier_extraction_1d()create_boundary_qp()create_connectivity()create_connectivity_1d()eval_bernstein_basis()eval_mapping_data_in_qp()eval_nurbs_basis_tp()eval_variable_in_qp()get_bezier_element_entities()get_bezier_topology()get_facet_axes()get_patch_box_regions()get_raveled_index()get_surface_degrees()get_unraveled_indices()tensor_product()
- sfepy.discrete.iga.io module
- sfepy.discrete.iga.mappings module
- sfepy.discrete.iga.plot_nurbs module
- sfepy.discrete.iga.utils module
sfepy.discrete.structural sub-package¶
sfepy.homogenization package¶
- sfepy.homogenization.band_gaps_app module
- sfepy.homogenization.coefficients module
- sfepy.homogenization.coefs_base module
CoefDimCoefDimDimCoefDimSymCoefDummyCoefEvalCoefExprParCoefMNCoefNCoefNonSymCoefNonSymNonSymCoefNoneCoefOneCoefSumCoefSymCoefSymDimCoefSymSymCorrDimCorrDimDimCorrEqParCorrEvalCorrMiniAppCorrNCorrNNCorrOneCorrSetBCSCorrSolutionMiniAppBaseOnesDimShapeDimShapeDimDimTSTimesVolumeFractions
- sfepy.homogenization.coefs_phononic module
AcousticMassLiquidTensorAcousticMassTensorAppliedLoadTensorBandGapsChristoffelAcousticTensorDensityVolumeInfoEigenmomentaPhaseVelocityPolarizationAnglesSchurEVPSimpleEVPcompute_cat_dim_dim()compute_cat_dim_sym()compute_cat_sym_sym()compute_eigenmomenta()cut_freq_range()describe_gaps()detect_band_gaps()find_zero()get_callback()get_gap_ranges()get_log_freqs()get_ranges()split_chunks()
- sfepy.homogenization.convolutions module
- sfepy.homogenization.engine module
- sfepy.homogenization.homogen_app module
- sfepy.homogenization.micmac module
- sfepy.homogenization.recovery module
add_strain_rs()add_stress_p()combine_scalar_grad()compute_mac_stress_part()compute_micro_u()compute_p_corr_steady()compute_p_corr_time()compute_p_from_macro()compute_stress_strain_u()compute_u_corr_steady()compute_u_corr_time()compute_u_from_macro()convolve_field_scalar()convolve_field_sym_tensor()destroy_pool()get_output_suffix()get_recovery_points()recover_bones()recover_micro_hook()recover_paraflow()save_recovery_region()
- sfepy.homogenization.utils module
sfepy.linalg package¶
sfepy.mechanics package¶
- sfepy.mechanics.contact_bodies module
- sfepy.mechanics.elastic_constants module
- sfepy.mechanics.matcoefs module
ElasticConstantsTransformToPlanebulk_from_lame()bulk_from_youngpoisson()lame_from_stiffness()lame_from_youngpoisson()stiffness_from_lame()stiffness_from_lame_mixed()stiffness_from_youngpoisson()stiffness_from_youngpoisson_mixed()stiffness_from_yps_ortho3()wave_speeds_from_youngpoisson()youngpoisson_from_stiffness()youngpoisson_from_wave_speeds()
- sfepy.mechanics.membranes module
- sfepy.mechanics.shell10x module
- sfepy.mechanics.tensors module
- sfepy.mechanics.units module
- sfepy.mechanics.extmods.ccontres module
sfepy.mesh package¶
sfepy.parallel package¶
- sfepy.parallel.evaluate module
- sfepy.parallel.parallel module
assemble_mtx_to_petsc()assemble_rhs_to_petsc()call_in_rank_order()create_gather_scatter()create_gather_to_zero()create_local_petsc_vector()create_petsc_matrix()create_petsc_system()create_prealloc_data()create_task_dof_maps()distribute_field_dofs()distribute_fields_dofs()expand_dofs()get_composite_sizes()get_inter_facets()get_local_ordering()get_sizes()init_petsc_args()partition_mesh()setup_composite_dofs()verify_task_dof_maps()view_petsc_local()
- sfepy.parallel.plot_parallel_dofs module
sfepy.postprocess package¶
sfepy.solvers package¶
- sfepy.solvers.auto_fallback module
- sfepy.solvers.eigen module
- sfepy.solvers.ls module
- sfepy.solvers.nls module
- sfepy.solvers.optimize module
- sfepy.solvers.oseen module
- sfepy.solvers.qeigen module
- sfepy.solvers.semismooth_newton module
- sfepy.solvers.solvers module
- sfepy.solvers.ts module
- sfepy.solvers.ts_controllers module
- sfepy.solvers.ts_solvers module
sfepy.terms package¶
- Term Overview
- sfepy.terms.terms module
- sfepy.terms.terms_adj_navier_stokes module
AdjConvect1TermAdjConvect2TermAdjDivGradTermNSOFMinGradTermNSOFSurfMinDPressDiffTermNSOFSurfMinDPressTermSDConvectTermSDDivGradTermSDDivTermSDDotTermSDGradDivStabilizationTermSDPSPGCStabilizationTermSDPSPGPStabilizationTermSDSUPGCStabilizationTermSUPGCAdjStabilizationTermSUPGPAdj1StabilizationTermSUPGPAdj2StabilizationTermgrad_as_vector()
- sfepy.terms.terms_basic module
- sfepy.terms.terms_biot module
- sfepy.terms.terms_compat module
CauchyStrainSTermDSumNodalValuesTermDSurfaceFluxTermDSurfaceMomentTermDVolumeSurfaceTermDotSurfaceProductTermDotVolumeProductTermIntegrateSurfaceMatTermIntegrateSurfaceOperatorTermIntegrateSurfaceTermIntegrateVolumeMatTermIntegrateVolumeOperatorTermIntegrateVolumeTermSDVolumeDotTermSurfaceDivTermSurfaceGradTermSurfaceTermVolumeXTerm
- sfepy.terms.terms_constraints module
- sfepy.terms.terms_contact module
- sfepy.terms.terms_dg module
- sfepy.terms.terms_diffusion module
- sfepy.terms.terms_dot module
- sfepy.terms.terms_elastic module
CauchyStrainTermCauchyStressETHTermCauchyStressTHTermCauchyStressTermElasticWaveCauchyTermElasticWaveTermLinearDRotSpringTermLinearDSpringTermLinearElasticETHTermLinearElasticIsotropicTermLinearElasticTHTermLinearElasticTermLinearPrestressTermLinearSpringTermLinearStrainFiberTermLinearTrussInternalForceTermLinearTrussTermNonsymElasticTermSDLinearElasticTerm
- sfepy.terms.terms_electric module
- sfepy.terms.terms_fibres module
- sfepy.terms.terms_flexo module
- sfepy.terms.terms_hyperelastic_base module
- sfepy.terms.terms_hyperelastic_tl module
BulkActiveTLTermBulkPenaltyTLTermBulkPressureTLTermDiffusionTLTermGenYeohTLTermHyperElasticSurfaceTLBaseHyperElasticSurfaceTLFamilyDataHyperElasticTLBaseHyperElasticTLFamilyDataMooneyRivlinTLTermNeoHookeanTLTermOgdenTLTermSurfaceFluxTLTermSurfaceTractionTLTermVolumeSurfaceTLTermVolumeTLTerm
- sfepy.terms.terms_hyperelastic_ul module
- sfepy.terms.terms_jax module
LinearElasticLADTermLinearElasticYPADTermMassADTermNeoHookeanTLADTermOgdenTLADTermceval_elasticity_l()ceval_elasticity_yp()ceval_mass()ceval_neohook()ceval_neohook0()ceval_ogden()eval_alpha_ogden()eval_density_mass()eval_elasticity_l()eval_elasticity_yp()eval_jac_elasticity_l()eval_jac_elasticity_yp()eval_jac_mass()eval_jac_neohook()eval_jac_ogden()eval_lam_elasticity_l()eval_mass()eval_mu_elasticity_l()eval_mu_neohook()eval_mu_ogden()eval_neohook()eval_ogden()eval_poisson_elasticity_yp()eval_young_elasticity_yp()get_neohook_strain_energy()get_neohook_strain_energy_f()get_neohook_stress_1pk()get_neohook_stress_2pk()get_ogden_strain_energy_f()get_ogden_stress_1pk()get_state_per_cell()get_strain()get_stress()
- sfepy.terms.terms_mass module
- sfepy.terms.terms_membrane module
- sfepy.terms.terms_multilinear module
ECauchyStressTermEConvectTermEDiffusionTermEDivGradTermEDivTermEDotTermEGradTermEIntegrateOperatorTermELaplaceTermELinearConvectTermELinearElasticTermELinearTractionTermENonPenetrationPenaltyTermENonSymElasticTermEScalarDotMGradScalarTermEStokesTermETermBaseExpressionArgExpressionBuilderStokesTractionTermSurfaceFluxOperatorTermSurfacePiezoFluxOperatorTermSurfacePiezoFluxTermappend_all()collect_modifiers()find_free_indices()get_einsum_ops()get_loop_indices()get_output_shape()get_sizes()get_slice_ops()parse_term_expression()sym2nonsym()
- sfepy.terms.terms_navier_stokes module
- sfepy.terms.terms_piezo module
- sfepy.terms.terms_point module
- sfepy.terms.terms_sensitivity module
- sfepy.terms.terms_shells module
- sfepy.terms.terms_surface module
- sfepy.terms.terms_th module
- sfepy.terms.terms_volume module
- sfepy.terms.utils module
- sfepy.terms.extmods.terms module
actBfT()d_biot_div()d_diffusion()d_laplace()d_lin_elastic()d_of_nsMinGrad()d_of_nsSurfMinDPress()d_piezo_coupling()d_sd_convect()d_sd_diffusion()d_sd_div()d_sd_div_grad()d_sd_lin_elastic()d_sd_st_grad_div()d_sd_st_pspg_c()d_sd_st_pspg_p()d_sd_st_supg_c()d_sd_volume_dot()d_surface_flux()d_tl_surface_flux()d_tl_volume_surface()d_volume_surface()de_cauchy_strain()de_cauchy_stress()de_he_rtm()di_surface_moment()dq_cauchy_strain()dq_def_grad()dq_div_vector()dq_finite_strain_tl()dq_finite_strain_ul()dq_grad()dq_state_in_qp()dq_tl_finite_strain_surface()dq_tl_he_stress_bulk()dq_tl_he_stress_bulk_active()dq_tl_he_stress_mooney_rivlin()dq_tl_he_stress_neohook()dq_tl_he_tan_mod_bulk()dq_tl_he_tan_mod_bulk_active()dq_tl_he_tan_mod_mooney_rivlin()dq_tl_he_tan_mod_neohook()dq_tl_stress_bulk_pressure()dq_tl_tan_mod_bulk_pressure_u()dq_ul_he_stress_bulk()dq_ul_he_stress_mooney_rivlin()dq_ul_he_stress_neohook()dq_ul_he_tan_mod_bulk()dq_ul_he_tan_mod_mooney_rivlin()dq_ul_he_tan_mod_neohook()dq_ul_stress_bulk_pressure()dq_ul_tan_mod_bulk_pressure_u()dw_adj_convect1()dw_adj_convect2()dw_biot_div()dw_biot_grad()dw_convect_v_grad_s()dw_diffusion()dw_diffusion_r()dw_div()dw_electric_source()dw_grad()dw_he_rtm()dw_laplace()dw_lin_convect()dw_lin_elastic()dw_lin_prestress()dw_lin_strain_fib()dw_nonsym_elastic()dw_piezo_coupling()dw_st_adj1_supg_p()dw_st_adj2_supg_p()dw_st_adj_supg_c()dw_st_grad_div()dw_st_pspg_c()dw_st_supg_c()dw_st_supg_p()dw_surface_flux()dw_surface_ltr()dw_surface_s_v_dot_n()dw_surface_v_dot_n_s()dw_tl_diffusion()dw_tl_surface_traction()dw_tl_volume()dw_ul_volume()dw_v_dot_grad_s_sw()dw_v_dot_grad_s_vw()dw_volume_dot_scalar()dw_volume_dot_vector()dw_volume_lvf()errclear()he_eval_from_mtx()he_residuum_from_mtx()mulAB_integrate()sym2nonsym()term_ns_asm_convect()term_ns_asm_div_grad()
Scripts¶
- sfepy.scripts.blockgen module
- sfepy.scripts.convert_mesh module
- sfepy.scripts.cylindergen module
- sfepy.scripts.gen_iga_patch module
- sfepy.scripts.gen_mesh module
- sfepy.scripts.gen_mesh_prev module
- sfepy.scripts.plot_condition_numbers module
- sfepy.scripts.plot_logs module
- sfepy.scripts.plot_mesh module
- sfepy.scripts.plot_quadratures module
- sfepy.scripts.plot_times module
- sfepy.scripts.probe module
- sfepy.scripts.resview module
- Examples
FieldOptsToListActionOptsToListActionStoreNumberActionadd_mat_id_to_grid()ensure3d()get_camera_position()get_nonzero_norm()main()make_cells_from_conn()make_glyphs()make_grid_from_mesh()make_title()parse_options()print_camera_position()pv_plot()read_mesh()read_probes_as_annotations()
- sfepy.scripts.run_tests module
- sfepy.scripts.simple module
Tests¶
- sfepy.tests.conftest module
- sfepy.tests.test_assembling module
- sfepy.tests.test_base module
- sfepy.tests.test_cmesh module
- sfepy.tests.test_conditions module
- sfepy.tests.test_declarative_examples module
- sfepy.tests.test_dg_field module
- sfepy.tests.test_dg_terms_calls module
- sfepy.tests.test_domain module
- sfepy.tests.test_ed_solvers module
- sfepy.tests.test_eigenvalue_solvers module
- sfepy.tests.test_elasticity_small_strain module
- sfepy.tests.test_fem module
- sfepy.tests.test_functions module
- sfepy.tests.test_high_level module
- sfepy.tests.test_homogenization_engine module
- sfepy.tests.test_homogenization_perfusion module
- sfepy.tests.test_hyperelastic_tlul module
- sfepy.tests.test_io module
- sfepy.tests.test_laplace_unit_disk module
- sfepy.tests.test_laplace_unit_square module
- sfepy.tests.test_lcbcs module
- sfepy.tests.test_linalg module
- sfepy.tests.test_linear_solvers module
- sfepy.tests.test_linearization module
- sfepy.tests.test_log module
- sfepy.tests.test_matcoefs module
- sfepy.tests.test_mesh_expand module
- sfepy.tests.test_mesh_generators module
- sfepy.tests.test_mesh_interp module
- sfepy.tests.test_mesh_smoothing module
- sfepy.tests.test_meshio module
- sfepy.tests.test_msm_laplace module
- sfepy.tests.test_msm_symbolic module
- sfepy.tests.test_normals module
- sfepy.tests.test_parsing module
- sfepy.tests.test_poly_spaces module
- sfepy.tests.test_projections module
- sfepy.tests.test_quadratures module
- sfepy.tests.test_ref_coors module
- sfepy.tests.test_refine_hanging module
- sfepy.tests.test_regions module
- sfepy.tests.test_semismooth_newton module
- sfepy.tests.test_sparse module
- sfepy.tests.test_splinebox module
- sfepy.tests.test_tensors module
- sfepy.tests.test_term_call_modes module
- sfepy.tests.test_term_consistency module
- sfepy.tests.test_term_sensitivity module
- sfepy.tests.test_units module
- sfepy.tests.test_volume module
Tools¶
- tools/build_helpers.py script
- tools/gen_field_table.py script
- tools/gen_gallery.py script
- tools/gen_legendre_simplex_base.py script
- tools/gen_lobatto1d_c.py script
- tools/gen_release_notes.py script
- tools/gen_serendipity_basis.py script
- tools/gen_solver_table.py script
- tools/gen_term_table.py script
- tools/install_data.py script
- tools/show_authors.py script
- tools/show_terms_use.py script
- tools/sync_module_docs.py script
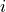 -th vector component
-th vector component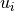
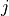 -th coordinate component
-th coordinate component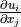
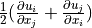
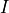 is the vector
component
is the vector
component