sfepy.terms.terms_surface module¶
- class sfepy.terms.terms_surface.ContactPlaneTerm(*args, **kwargs)[source]¶
Small deformation elastic contact plane term with penetration penalty.
The plane is given by an anchor point
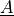 and a normal
and a normal
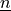 . The contact occurs in points that orthogonally project onto
the plane into a polygon given by orthogonal projections of boundary points
. The contact occurs in points that orthogonally project onto
the plane into a polygon given by orthogonal projections of boundary points
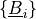 ,
, 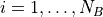 on the plane. In such
points, a penetration distance
on the plane. In such
points, a penetration distance 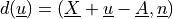 is computed, and a force
is computed, and a force 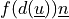 is
applied. The force depends on the non-negative parameters
is
applied. The force depends on the non-negative parameters 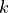 (stiffness) and
(stiffness) and 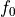 (force at zero penetration):
(force at zero penetration):If
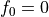 :
: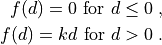
If
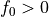 :
: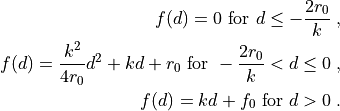
In this case the dependence
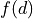 is smooth, and a (small) force
is applied even for (small) negative penetrations:
is smooth, and a (small) force
is applied even for (small) negative penetrations: 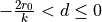 .
.
- Definition:
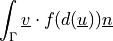
- Call signature:
dw_contact_plane
(material_f, material_n, material_a, material_b, virtual, state)- Arguments:
material_f :
![[k, f_0]](../../../_images/math/9e9e3be36ed826cad5e4ef0ce0e82584d8bd24fe.png)
material_n :
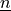 (special)
(special)material_a :
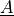 (special)
(special)material_b :
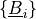 ,
, 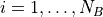 (special)
(special)virtual :

state :

- arg_shapes = {'material_a': '.: D', 'material_b': '.: N, D', 'material_f': '1, 2', 'material_n': '.: D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material_f', 'material_n', 'material_a', 'material_b', 'virtual', 'state')¶
- geometries = ['3_4', '3_8']¶
- get_fargs(force_pars, normal, anchor, bounds, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'facet'¶
- name = 'dw_contact_plane'¶
- class sfepy.terms.terms_surface.ContactSphereTerm(*args, **kwargs)[source]¶
Small deformation elastic contact sphere term with penetration penalty.
The sphere is given by a centre point
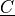 and a radius
and a radius
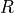 . The contact occurs in points that are closer to
. The contact occurs in points that are closer to 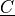 than
than 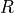 . In such points, a penetration distance
. In such points, a penetration distance 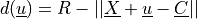 is computed, and a force
is computed, and a force
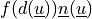 is applied, where
is applied, where 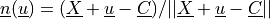 . The force
depends on the non-negative parameters
. The force
depends on the non-negative parameters 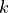 (stiffness) and
(stiffness) and
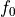 (force at zero penetration):
(force at zero penetration):If
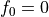 :
: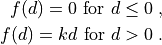
If
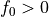 :
: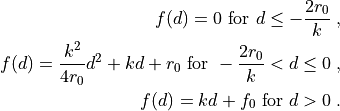
In this case the dependence
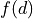 is smooth, and a (small) force
is applied even for (small) negative penetrations:
is smooth, and a (small) force
is applied even for (small) negative penetrations: 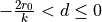 .
.
- Definition:
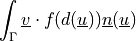
- Call signature:
dw_contact_sphere
(material_f, material_c, material_r, virtual, state)- Arguments:
material_f :
![[k, f_0]](../../../_images/math/9e9e3be36ed826cad5e4ef0ce0e82584d8bd24fe.png)
material_c :
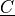 (special)
(special)material_r :
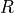 (special)
(special)virtual :

state :

- arg_shapes = {'material_c': '.: D', 'material_f': '1, 2', 'material_r': '.: 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material_f', 'material_c', 'material_r', 'virtual', 'state')¶
- geometries = ['3_4', '3_8']¶
- get_fargs(force_pars, centre, radius, virtual, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'facet'¶
- name = 'dw_contact_sphere'¶
- class sfepy.terms.terms_surface.LinearTractionTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear traction forces, where, depending on dimension of ‘material’ argument,
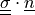 is
is
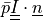 for a given scalar pressure,
for a given scalar pressure,
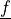 for a traction vector, and itself for a stress tensor.
for a traction vector, and itself for a stress tensor.The material parameter can have one of the following shapes: 1 or (1, 1), (D, 1), (S, 1) in all modes, or (D, D) in the eval mode only. The symmetric tensor storage (S, 1) is as follows: in 3D S = 6 and the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) ,
in 2D S = 3 and the indices ordered as
,
in 2D S = 3 and the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.- Definition:
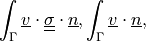
- Call signature:
dw_surface_ltr
(opt_material, virtual)(opt_material, parameter)- Arguments:
material :
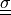
virtual :

- arg_shapes = [{'opt_material': 'S, 1', 'parameter': 'D', 'virtual': ('D', None)}, {'opt_material': 'D, 1'}, {'opt_material': '1, 1'}, {'opt_material': 'D, D'}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual'), ('opt_material', 'parameter'))¶
- integration = 'facet'¶
- modes = ('weak', 'eval')¶
- name = 'dw_surface_ltr'¶
- class sfepy.terms.terms_surface.SDLinearTractionTerm(name, arg_str, integral, region, **kwargs)[source]¶
Sensitivity of the linear traction term.
- Definition:
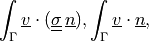
- Call signature:
ev_sd_surface_ltr
(opt_material, parameter, parameter_mv)- Arguments:
material :
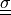
parameter :

- arg_shapes = [{'opt_material': 'S, 1', 'parameter': 'D', 'parameter_mv': 'D'}, {'opt_material': '1, 1'}, {'opt_material': 'D, 1'}, {'opt_material': 'D, D'}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'parameter', 'parameter_mv')¶
- get_eval_shape(traction, par_u, par_mv, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'facet'¶
- name = 'ev_sd_surface_ltr'¶
- class sfepy.terms.terms_surface.SDSufaceIntegrateTerm(name, arg_str, integral, region, **kwargs)[source]¶
Sensitivity of scalar traction.
- Definition:
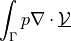
- Call signature:
ev_sd_surface_integrate
(parameter, parameter_mv)- Arguments:
parameter :

parameter_mv :
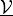
- arg_shapes = {'parameter': 1, 'parameter_mv': 'D'}¶
- arg_types = ('parameter', 'parameter_mv')¶
- integration = 'facet'¶
- name = 'ev_sd_surface_integrate'¶
- class sfepy.terms.terms_surface.SufaceNormalDotTerm(name, arg_str, integral, region, **kwargs)[source]¶
“Scalar traction” term, (weak form).
- Definition:
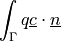
- Call signature:
dw_surface_ndot
(material, virtual)(material, parameter)- Arguments:
material :
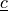
virtual :
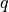
- arg_shapes = {'material': 'D, 1', 'parameter': 1, 'virtual': (1, None)}¶
- arg_types = (('material', 'virtual'), ('material', 'parameter'))¶
- integration = 'facet'¶
- modes = ('weak', 'eval')¶
- name = 'dw_surface_ndot'¶
- class sfepy.terms.terms_surface.SurfaceJumpTerm(name, arg_str, integral, region, **kwargs)[source]¶
Interface jump condition.
- Definition:
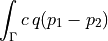
- Call signature:
dw_jump
(opt_material, virtual, state_1, state_2)- Arguments:
material :

virtual :
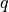
state_1 :
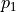
state_2 :
- arg_shapes = [{'opt_material': '1, 1', 'state_1': 1, 'state_2': 1, 'virtual': (1, None)}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'virtual', 'state_1', 'state_2')¶
- get_fargs(coef, virtual, state1, state2, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- integration = 'facet'¶
- name = 'dw_jump'¶