sfepy.terms.terms_point module¶
- class sfepy.terms.terms_point.ConcentratedPointLoadTerm(name, arg_str, integral, region, **kwargs)[source]¶
Concentrated point load term.
The load value must be given in form of a special material parameter (name prefixed with ‘.’), e.g. (in 2D):
'load' : ({'.val' : [0.0, 1.0]},)
This term should be used with special care, as it bypasses the usual evaluation in quadrature points. It should only be used with nodal FE basis. The number of rows of the load must be equal to the number of nodes in the region and the number of columns equal to the field dimension.
- Definition:
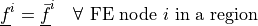
- Call signature:
dw_point_load
(material, virtual)- Arguments:
material :
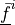
virtual :
 ,
,
- arg_shapes = {'material': '.: N', 'virtual': ('N', None)}¶
- arg_types = ('material', 'virtual')¶
- integration = 'point'¶
- name = 'dw_point_load'¶
- class sfepy.terms.terms_point.LinearPointSpringTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linear springs constraining movement of FE nodes in a region; to use as a relaxed Dirichlet boundary conditions.
- Definition:
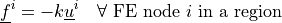
- Call signature:
dw_point_lspring
(material, virtual, state)- Arguments:
material :
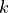
virtual :

state :

- arg_shapes = {'material': '.: 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- integration = 'point'¶
- name = 'dw_point_lspring'¶