sfepy.terms.terms_hyperelastic_ul module¶
- class sfepy.terms.terms_hyperelastic_ul.BulkPenaltyULTerm(*args, **kwargs)[source]¶
Hyperelastic bulk penalty term. Stress
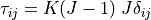 .
.- Definition:
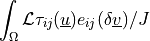
- Call signature:
dw_ul_bulk_penalty
(material, virtual, state)- Arguments:
material :
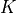
virtual :

state :

- family_data_names = ['det_f']¶
- name = 'dw_ul_bulk_penalty'¶
- static stress_function(out, mat, det_f)¶
- static tan_mod_function(out, mat, det_f)¶
- class sfepy.terms.terms_hyperelastic_ul.BulkPressureULTerm(*args, **kwargs)[source]¶
Hyperelastic bulk pressure term. Stress
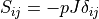 .
.- Definition:
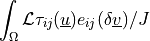
- Call signature:
dw_ul_bulk_pressure
(virtual, state, state_p)- Arguments:
virtual :

state :

state_p :

- arg_geometry_types = {('state_p', None): {'facet_extra': 'facet'}}¶
- arg_shapes = {'state': 'D', 'state_p': 1, 'virtual': ('D', 'state')}¶
- arg_types = ('virtual', 'state', 'state_p')¶
- family_data_names = ['det_f', 'sym_b']¶
- static family_function(mtx_f, det_f, vec_bs, tr_b, in_2b, vec_es, state, cmap, conn)¶
- get_eval_shape(virtual, state, state_p, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_ul_bulk_pressure'¶
- static stress_function(out, pressure_qp, det_f)¶
- static tan_mod_u_function(out, pressure_qp, det_f)¶
- static weak_dp_function(out, det_f, cmap_s, cmap_v, transpose, mode)¶
- static weak_function(out, stress, tan_mod, mtx_f, det_f, cmap, is_diff, mode_ul)¶
- class sfepy.terms.terms_hyperelastic_ul.CompressibilityULTerm(*args, **kwargs)[source]¶
Compressibility term for the updated Lagrangian formulation
- Definition:
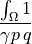
- Call signature:
dw_ul_compressible
(material, virtual, state, parameter_u)- Arguments:
material :
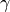
virtual :
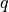
state :

parameter_u :
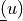
- arg_geometry_types = {('state', None): {'facet_extra': 'facet'}, ('virtual', None): {'facet_extra': 'facet'}}¶
- arg_shapes = {'material': '1, 1', 'parameter_u': 'D', 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = ('material', 'virtual', 'state', 'parameter_u')¶
- family_data_names = ['mtx_f', 'det_f']¶
- static function(out, coef, val_qp, rcmap, ccmap, is_diff)¶
- get_fargs(bulk, virtual, state, parameter_u, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_ul_compressible'¶
- class sfepy.terms.terms_hyperelastic_ul.HyperElasticULBase(*args, **kwargs)[source]¶
Base class for all hyperelastic terms in UL formulation family.
The subclasses should have the following static method attributes: - stress_function() (the stress) - tan_mod_function() (the tangent modulus)
- get_family_data = HyperElasticULFamilyData¶
- hyperelastic_mode = 1¶
- static weak_function(out, stress, tan_mod, mtx_f, det_f, cmap, is_diff, mode_ul)¶
- class sfepy.terms.terms_hyperelastic_ul.HyperElasticULFamilyData(**kwargs)[source]¶
Family data for UL formulation.
- cache_name = 'ul_common'¶
- data_names = ('mtx_f', 'det_f', 'sym_b', 'tr_b', 'in2_b', 'green_strain')¶
- static family_function(mtx_f, det_f, vec_bs, tr_b, in_2b, vec_es, state, cmap, conn)¶
- class sfepy.terms.terms_hyperelastic_ul.HyperelasticByFunULTerm(*args, **kwargs)[source]¶
General hyperelastic term: the tangent modulus and the stress tensor are calculated by a user defined function
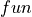 .
.- Definition:
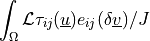
- Call signature:
dw_ul_he_by_fun
(fun, virtual, state)- Arguments:
material :
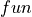
virtual :

state :

- arg_shapes = [{'fun': <function HyperelasticByFunULTerm.<lambda>>, 'state': 'D', 'virtual': ('D', 'state')}]¶
- arg_types = ('fun', 'virtual', 'state')¶
- family_data_names = ['mtx_f', 'det_f', 'sym_b', 'tr_b', 'in2_b', 'green_strain']¶
- name = 'dw_ul_he_by_fun'¶
- class sfepy.terms.terms_hyperelastic_ul.MooneyRivlinULTerm(*args, **kwargs)[source]¶
Hyperelastic Mooney-Rivlin term.
- Definition:
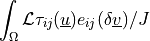
- Call signature:
dw_ul_he_mooney_rivlin
(material, virtual, state)- Arguments:
material :

virtual :

state :

- family_data_names = ['det_f', 'tr_b', 'sym_b', 'in2_b']¶
- name = 'dw_ul_he_mooney_rivlin'¶
- static stress_function(out, mat, det_f, tr_b, vec_bs, in_2b)¶
- static tan_mod_function(out, mat, det_f, tr_b, vec_bs, in_2b)¶
- class sfepy.terms.terms_hyperelastic_ul.NeoHookeanULTerm(*args, **kwargs)[source]¶
Hyperelastic neo-Hookean term. Effective stress
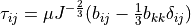 .
.- Definition:
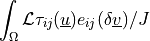
- Call signature:
dw_ul_he_neohook
(material, virtual, state)- Arguments:
material :
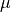
virtual :

state :

- family_data_names = ['det_f', 'tr_b', 'sym_b']¶
- name = 'dw_ul_he_neohook'¶
- static stress_function(out, mat, det_f, tr_b, vec_bs)¶
- static tan_mod_function(out, mat, det_f, tr_b, vec_bs)¶
- class sfepy.terms.terms_hyperelastic_ul.VolumeULTerm(*args, **kwargs)[source]¶
Volume term (weak form) in the updated Lagrangian formulation.
- Definition:
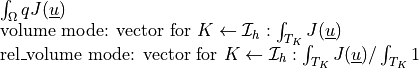
- Call signature:
dw_ul_volume
(virtual, state)- Arguments:
virtual :
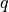
state :

- arg_geometry_types = {('virtual', None): {'facet_extra': 'facet'}}¶
- arg_shapes = {'state': 'D', 'virtual': (1, None)}¶
- arg_types = ('virtual', 'state')¶
- family_data_names = ['mtx_f', 'det_f']¶
- static function(out, det_f, cmap_s, cmap_v, transpose, mode)¶
- name = 'dw_ul_volume'¶