navier_stokes/stabilized_navier_stokes.py¶

Description

Stabilized Navier-Stokes problem with grad-div, SUPG and PSPG stabilization solved by a custom Oseen solver.

The stabilization terms are described in [1].

[1] G. Matthies and G. Lube. On streamline-diffusion methods of inf-sup stable discretisations of the generalised Oseen problem. Number 2007-02 in Preprint Series of Institut fuer Numerische und Angewandte Mathematik, Georg-August-Universitaet Goettingen, 2007.

Find $\ul{u}$ , $p$ such that:

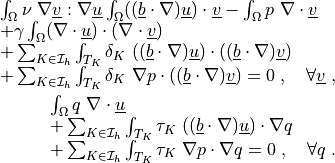
$\begin{array}{l} \int_{\Omega} \nu\ \nabla \ul{v} : \nabla \ul{u} \int_{\Omega} ((\ul{b} \cdot \nabla) \ul{u}) \cdot \ul{v} - \int_{\Omega} p\ \nabla \cdot \ul{v} \\ + \gamma \int_{\Omega} (\nabla\cdot\ul{u}) \cdot (\nabla\cdot\ul{v}) \\ + \sum_{K \in \Ical_h}\int_{T_K} \delta_K\ ((\ul{b} \cdot \nabla) \ul{u})\cdot ((\ul{b} \cdot \nabla) \ul{v}) \\ + \sum_{K \in \Ical_h}\int_{T_K} \delta_K\ \nabla p\cdot ((\ul{b} \cdot \nabla) \ul{v}) = 0 \;, \quad \forall \ul{v} \;, \end{array} \begin{array}{l} \int_{\Omega} q\ \nabla \cdot \ul{u} \\ + \sum_{K \in \Ical_h}\int_{T_K} \tau_K\ ((\ul{b} \cdot \nabla) \ul{u}) \cdot \nabla q \\ + \sum_{K \in \Ical_h}\int_{T_K} \tau_K\ \nabla p \cdot \nabla q = 0 \;, \quad \forall q \;. \end{array}$

../_images/navier_stokes-stabilized_navier_stokes1.png

source code

r"""
Stabilized Navier-Stokes problem with grad-div, SUPG and PSPG stabilization
solved by a custom Oseen solver.

The stabilization terms are described in [1].

[1] G. Matthies and G. Lube. On streamline-diffusion methods of inf-sup stable
discretisations of the generalised Oseen problem. Number 2007-02 in Preprint
Series of Institut fuer Numerische und Angewandte Mathematik,
Georg-August-Universitaet Goettingen, 2007.

Find :math:`\ul{u}`, :math:`p` such that:

.. math::
    \begin{array}{l}
    \int_{\Omega} \nu\ \nabla \ul{v} : \nabla \ul{u}
    \int_{\Omega} ((\ul{b} \cdot \nabla) \ul{u}) \cdot \ul{v}
    - \int_{\Omega} p\ \nabla \cdot \ul{v} \\
    + \gamma \int_{\Omega} (\nabla\cdot\ul{u}) \cdot (\nabla\cdot\ul{v}) \\
    + \sum_{K \in \Ical_h}\int_{T_K} \delta_K\ ((\ul{b} \cdot \nabla)
      \ul{u})\cdot ((\ul{b} \cdot \nabla) \ul{v}) \\
    + \sum_{K \in \Ical_h}\int_{T_K} \delta_K\ \nabla p\cdot ((\ul{b} \cdot
      \nabla) \ul{v})
    = 0
    \;, \quad \forall \ul{v} \;,
    \end{array}

    \begin{array}{l}
    \int_{\Omega} q\ \nabla \cdot \ul{u} \\
    + \sum_{K \in \Ical_h}\int_{T_K} \tau_K\ ((\ul{b} \cdot \nabla) \ul{u})
      \cdot \nabla q \\
    + \sum_{K \in \Ical_h}\int_{T_K} \tau_K\ \nabla p \cdot \nabla q
    = 0
    \;, \quad \forall q \;.
    \end{array}
"""
from __future__ import absolute_import
from sfepy.solvers.oseen import StabilizationFunction
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/3d/elbow2.mesh'

options = {
    'solution' : 'steady',
    'nls' : 'oseen',
    'ls' : 'ls',
}

regions = {
    'Omega' : 'all',
    'Walls' : ('vertices of surface -v (r.Outlet +v r.Inlet)', 'facet'),
    'Inlet' : ('vertices by cinc0', 'facet'),
    'Outlet' : ('vertices by cinc1', 'facet'),
}

fields = {
    'velocity' : ('real', 3, 'Omega', 1),
    'pressure' : ('real', 1, 'Omega', 1),
}

variables = {
    'u'   : ('unknown field',   'velocity', 0),
    'v'   : ('test field',      'velocity', 'u'),
    'b'   : ('parameter field', 'velocity', 'u'),
    'p'   : ('unknown field',   'pressure', 1),
    'q'   : ('test field',      'pressure', 'p'),
}

ebcs = {
    'Walls_velocity' : ('Walls', {'u.all' : 0.0}),
    'Inlet_velocity' : ('Inlet', {'u.1' : 1.0, 'u.[0,2]' : 0.0}),
}

materials = {
    'fluid' : ({'viscosity' : 1.25e-5,
                'density' : 1e0},),
    'stabil' : 'stabil',
}

integrals = {
    'i1' : 2,
    'i2' : 3,
}

##
# Stationary Navier-Stokes equations with grad-div, SUPG and PSPG stabilization.
equations = {
    'balance' :
    """  dw_div_grad.i2.Omega( fluid.viscosity, v, u )
       + dw_lin_convect.i2.Omega( v, b, u )
       - dw_stokes.i1.Omega( v, p )
       + dw_st_grad_div.i1.Omega( stabil.gamma, v, u )
       + dw_st_supg_c.i1.Omega( stabil.delta, v, b, u )
       + dw_st_supg_p.i1.Omega( stabil.delta, v, b, p )
       = 0""",
    'incompressibility' :
    """  dw_stokes.i1.Omega( u, q )
       + dw_st_pspg_c.i1.Omega( stabil.tau, q, b, u )
       + dw_st_pspg_p.i1.Omega( stabil.tau, q, p )
       = 0""",
}

solver_1 = {
    'name' : 'oseen',
    'kind' : 'nls.oseen',

    'stabil_mat' : 'stabil',

    'adimensionalize' : False,
    'check_navier_stokes_residual' : False,

    'i_max'      : 10,
    'eps_a'      : 1e-8,
    'eps_r'      : 1.0,
    'macheps'    : 1e-16,
    'lin_red'    : 1e-2, # Linear system error < (eps_a * lin_red).

    # Uncomment the following to get a convergence log.
    ## 'log'        : {'text' : 'oseen_log.txt',
    ##                 'plot' : 'oseen_log.png'},
}

solver_2 = {
    'name' : 'ls',
    'kind' : 'ls.scipy_direct',
}

##
# Functions.
import os.path as op
import sys

sys.path.append(data_dir) # Make installed example work.
import sfepy.examples.navier_stokes.utils as utils

cinc_name = 'cinc_' + op.splitext(op.basename(filename_mesh))[0]
cinc = getattr(utils, cinc_name)

name_map = {'p' : 'p', 'q' : 'q', 'u' : 'u', 'b' : 'b', 'v' : 'v',
            'fluid' : 'fluid', 'omega' : 'omega', 'i1' : 'i1', 'i2' : 'i2',
            'viscosity' : 'viscosity', 'velocity' : 'velocity',
            'gamma' : 'gamma', 'delta' : 'delta', 'tau' : 'tau'}

functions = {
    'cinc0' : (lambda coors, domain=None: cinc(coors, 0),),
    'cinc1' : (lambda coors, domain=None: cinc(coors, 1),),
    'stabil' : (StabilizationFunction(name_map),),
}