miscellaneous/refine_evp.py¶
Description
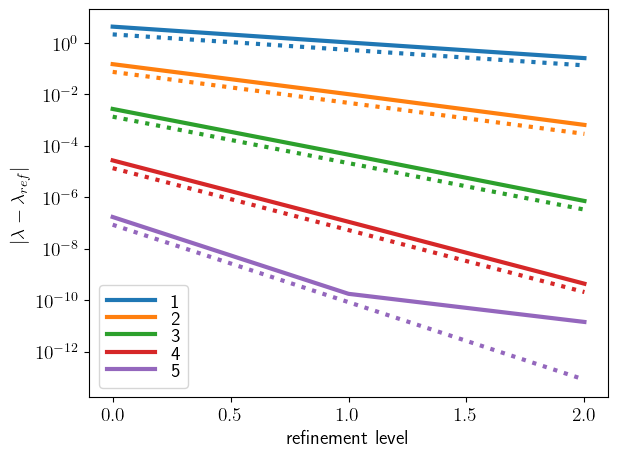
Plot the convergence of eigenvalues (or corresponding frequencies) of an eigenvalue problem to an analytical solution, when applying the uniform mesh refinement.
Uses the PRIMME eigenvalue solver by default (pip install primme).
Usage Examples¶
Run without the convergence analysis, use the spectral element method (SEM) basis of order 5:
sfepy-run sfepy/examples/miscellaneous/refine_evp.py -d order=5,basis=sem
Get help:
python3 sfepy/examples/miscellaneous/refine_evp.py -h
Plot the convergence of the smallest eigenvalue of the Laplace Dirichlet problem:
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2
Plot the convergence of the smallest frequency of the 1D elastic bar vibration problem, show relative errors:
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2 --kind=elasticity --transform=freqs --relative
Using the 1D elastic bar vibration problem, compare the SEM results with the FEM + row-sum mass matrix lumping. Plot also the sparsity patterns of the mass (M) and stiffness (K) matrices:
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2 --evps=primme --kind=elasticity-lumping --transform=freqs --relative --beta=1 --mass-lumping='row_sum' --sparsity python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2 --evps=primme --kind=elasticity --basis=sem --transform=freqs --relative --beta=0 --mass-lumping='none' --sparsity
"""
Plot the convergence of eigenvalues (or corresponding frequencies) of an
eigenvalue problem to an analytical solution, when applying the uniform
mesh refinement.
Uses the PRIMME eigenvalue solver by default (``pip install primme``).
Usage Examples
--------------
- Run without the convergence analysis, use the spectral element method (SEM)
basis of order 5::
sfepy-run sfepy/examples/miscellaneous/refine_evp.py -d order=5,basis=sem
- Get help::
python3 sfepy/examples/miscellaneous/refine_evp.py -h
- Plot the convergence of the smallest eigenvalue of the Laplace Dirichlet
problem::
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2
- Plot the convergence of the smallest frequency of the 1D elastic bar
vibration problem, show relative errors::
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2 --kind=elasticity --transform=freqs --relative
- Using the 1D elastic bar vibration problem, compare the SEM results with the
FEM + row-sum mass matrix lumping. Plot also the sparsity patterns of the
mass (M) and stiffness (K) matrices::
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2 --evps=primme --kind=elasticity-lumping --transform=freqs --relative --beta=1 --mass-lumping='row_sum' --sparsity
python3 sfepy/examples/miscellaneous/refine_evp.py --max-order=5 --max-refine=2 --evps=primme --kind=elasticity --basis=sem --transform=freqs --relative --beta=0 --mass-lumping='none' --sparsity
"""
from argparse import ArgumentParser, RawDescriptionHelpFormatter
import sys
import os.path as op
from functools import partial
from itertools import product
import numpy as nm
import matplotlib.pyplot as plt
from sfepy.base.base import output
from sfepy.base.conf import dict_from_string as parse_as_dict
from sfepy.discrete.fem.meshio import UserMeshIO
from sfepy.mesh.mesh_generators import gen_block_mesh
from sfepy.base.conf import ProblemConf
from sfepy.discrete import Problem
from sfepy.solvers import Solver
from sfepy.discrete.fem.poly_spaces import SEMTensorProductPolySpace
def define(order=1, refine=0, evps='primme', n_eigs=1, eigs_only=True,
kind='laplace', basis='lagrange', beta=1.0, mass_lumping='none',
transform='none', output_dir='output', **kwargs):
options = {
'evps' : evps,
'n_eigs' : n_eigs,
'eigs_only' : eigs_only,
'active_only' : True,
'refinement_level' : refine,
'output_dir' : output_dir,
}
if kind == 'laplace':
dims, shape, centre = [1.0, 1.0], [3, 3], [0.5, 0.5]
regions = {
'Omega' : 'all',
'Gamma' : ('vertices of surface', 'facet'),
}
materials = {
}
fields = {
'fu' : ('real', 'scalar', 'Omega', order, 'H1', basis),
}
variables = {
'u' : ('unknown field', 'fu', 0),
'v' : ('test field', 'fu', 'u'),
}
ebcs = {
'zeros' : ('Gamma', {'u.0' : 0.0}),
}
if basis != 'sem':
integrals = {
'i' : 2 * order,
}
else:
from sfepy.discrete.fem.geometry_element import GeometryElement
dim = len (dims)
gel = GeometryElement(f'{dim}_{2**dim}')
ps = SEMTensorProductPolySpace(None, gel, order)
integrals = {
'i' : ('custom', ps.node_coors, ps.node_weights),
}
equations = {
'lhs' : """dw_laplace.i.Omega(v, u)""",
'rhs' : """dw_dot.i.Omega(v, u)""",
}
def eval_exact(n_eigs):
num = int(nm.ceil(nm.sqrt(n_eigs)))
rng = range(1, num+1)
eigs = [(ir**2 + ic**2) * nm.pi**2 for ir, ic in product(rng, rng)]
return nm.array(sorted(eigs)[:n_eigs], dtype=nm.float64)
else:
import sfepy.mechanics.matcoefs as mc
dims, shape, centre = [1.0], [2], [0.5]
regions = {
'Omega' : 'all',
'Gamma' : ('vertices in (x < %.16e)' % 1e-8, 'facet'),
}
dim = len(dims)
young = 69e9
density = 2700.0
poisson = 0.0
plane = 'strain'
materials = {
'm' : ({
'rho' : density,
'D' : mc.stiffness_from_youngpoisson(
dim, young=young, poisson=poisson, plane=plane
),
},),
'c' : ({
'.beta' : beta,
'.mass_lumping' : mass_lumping,
},),
}
fields = {
'fu' : ('real', dim, 'Omega', order, 'H1', basis),
}
variables = {
'u' : ('unknown field', 'fu', 0),
'v' : ('test field', 'fu', 'u'),
}
ebcs = {
'zeros' : ('Gamma', {'u.all' : 0.0}),
}
if basis != 'sem':
integrals = {
'i' : 2 * order,
}
else:
from sfepy.discrete.fem.geometry_element import GeometryElement
dim = len(dims)
gel = GeometryElement(f'{dim}_{2**dim}')
ps = SEMTensorProductPolySpace(None, gel, order)
integrals = {
'i' : ('custom', ps.node_coors, ps.node_weights),
}
equations = {
'lhs' : """dw_lin_elastic.i.Omega(m.D, v, u)""",
'rhs' : """dw_dot.i.Omega(m.rho, v, u)""",
}
if kind == 'elasticity-lumping':
equations.update({
'rhs' : """de_mass.i.Omega(m.rho, c.mass_lumping, c.beta,
v, u)""",
})
def eval_exact(n_eigs):
c0 = nm.sqrt(young / density)
ns = nm.arange(1, n_eigs+1)
freqs = 0.5 * (ns - 0.5) * c0 / dims[0]
if transform == 'none':
eigs = (2 * nm.pi * freqs)**2
else:
eigs = freqs
return eigs
def mesh_hook(mesh, mode):
"""
Generate the block mesh.
"""
if mode == 'read':
mesh = gen_block_mesh(dims, shape, centre,
name='evp-test', verbose=False)
return mesh
elif mode == 'write':
pass
filename_mesh = UserMeshIO(mesh_hook)
solvers = {
'matlab': ('eig.matlab', {
'method': 'eigs',
'which': 'sm',
'eps': 1e-14,
}),
'primme' : ('eig.primme', {
'which' : 'SM',
# Prevent hanging with 1x1 matrices and tol = 1e-14.
'tol' : 1e-13 if refine == 0 else 1e-14,
}),
'scipy' : ('eig.scipy', {
'method' : 'eigsh',
'tol' : 1e-14,
# 'maxiter' : 150,
# Compute the eigenvalues near 0 (= the smallest eigenvalues) using
# the shift-invert mode.
'which' : 'LM',
'sigma' : 0.0,
}),
}
return locals()
def get_figname(name, options):
rel = 'r' if options.relative else 'a'
figname = (f'{name}-{options.kind}-{options.basis}-{options.evps}'
f'-{options.transform}-{rel}{options.fig_suffix}')
return figname
def parse_args(args=None):
helps = {}
opts = dict(
max_order = (1, 'max. approximation order'),
max_refine = (0, 'max. uniform refinement level'),
evps = ('primme', 'solver name'),
n_eigs = (1, 'number of eigenvalues'),
kind = (('laplace', 'elasticity', 'elasticity-lumping'), 'problem kind'),
basis = (('lagrange', 'lobatto', 'sem'), 'field basis'),
beta = (1.0, 'averaged mass matrix parameter'),
mass_lumping = ('none', 'mass matrix lumping algorithm'),
transform = (('none', 'freqs'), 'eigenvalues transformation'),
relative = (False, 'plot relative errors'),
sparsity = (False, 'plot sparsity patterns of matrices'),
fig_suffix = ('.pdf', 'file suffix for saving figures'),
plot_rc_params = ('', 'matplotlib resources'),
output_dir = ('output', 'output directory'),
show = (True, 'do not show matplotlib figures'),
shell = (False, 'run ipython shell after all computations'),
debug = (False,
'automatically start debugger when an exception is raised'),
)
parser = ArgumentParser(description=__doc__.rstrip(),
formatter_class=RawDescriptionHelpFormatter)
dhelp = ' [default: %(default)s]'
for key, (val, msg) in opts.items():
helps[key] = msg
action = 'store'
vtype = type(val)
choices = None
option = key
if val is True:
action = 'store_false'
option = 'no_' + key
elif val is False:
action = 'store_true'
elif isinstance(val, tuple):
choices = val
vtype = type(val[0])
val = val[0]
elif isinstance(val, list):
vtype = type(val[1])
val = val[0]
if action == 'store':
helps[key] += dhelp
parser.add_argument('--' + option.replace('_', '-'),
type=vtype,
action=action, dest=key, choices=choices,
default=val, help=helps[key])
else:
parser.add_argument('--' + option.replace('_', '-'),
action=action, dest=key,
default=val, help=helps[key])
options = parser.parse_args(args=args)
options.plot_rc_params = parse_as_dict(options.plot_rc_params)
return options, helps
def main():
options, helps = parse_args()
if options.debug:
from sfepy.base.base import debug_on_error; debug_on_error()
inodir = partial(op.join, options.output_dir)
orders = range(1, options.max_order + 1)
all_eigs = []
for order, refine in product(
orders,
range(options.max_refine + 1),
):
conf = ProblemConf.from_dict(define(order=order, refine=refine,
**vars(options)),
sys.modules[__name__])
pb = Problem.from_conf(conf)
pb.time_update()
mtx_a = pb.evaluate(pb.conf.equations['lhs'], mode='weak',
auto_init=True, dw_mode='matrix')
mtx_b = pb.evaluate(pb.conf.equations['rhs'], mode='weak',
dw_mode='matrix')
eig = Solver.any_from_conf(pb.get_solver_conf(options.evps))
n_eigs = min(mtx_a.shape[0], options.n_eigs)
try:
eigs = eig(mtx_a, mtx_b, n_eigs, eigenvectors=False)
eigs = nm.pad(eigs, (0, options.n_eigs - n_eigs), 'constant',
constant_values=(nm.nan, nm.nan))
except:
eigs = nm.full(options.n_eigs, nm.nan)
all_eigs.append(eigs)
eigs_nums = nm.array(all_eigs).reshape(
(options.max_order, -1, options.n_eigs)
)
eigs_ana = pb.conf.eval_exact(options.n_eigs)
if options.transform == 'freqs':
eigs_nums = nm.sqrt(eigs_nums) / (2 * nm.pi)
ref = nm.arange(options.max_refine + 1)
hs = 1.0 / 2.0**ref
plt.rcParams['text.usetex'] = True
plt.rcParams['font.size'] = 14
plt.rcParams['lines.linewidth'] = 3
plt.rcParams['legend.handlelength'] = 2.5
plt.rcParams['legend.labelspacing'] = 0.0
plt.rcParams.update(options.plot_rc_params)
x = r'\lambda' if options.transform == 'none' else 'f'
if options.relative:
ylabel = f'$|{x}/{x}_{{ref}} - 1|$'
else:
ylabel = f'$|{x} - {x}_{{ref}}|$'
for ie in range(options.n_eigs):
fig, ax = plt.subplots()
colors = plt.cm.tab10.colors
for io, order in enumerate(orders):
eigs_num = eigs_nums[io, :, ie]
eig_ana = eigs_ana[ie]
error = nm.abs(eigs_num - eig_ana)
if options.relative:
error /= eig_ana
output('order:', order)
output('analytical:', eig_ana)
output('numerical :', eigs_num)
t0 = error[0] / 2
terror = t0 * hs**(2 * order)
ax.semilogy(ref, error, color=colors[io], label=order)
ax.semilogy(ref, terror, color=colors[io], ls=':')
ax.set_xlabel('refinement level')
ax.set_ylabel(ylabel)
ax.legend()
fig.tight_layout()
fig.savefig(inodir(get_figname(f'h-refinement-{ie}', options)),
bbox_inches='tight')
if options.sparsity:
fig, ax = plt.subplots()
ax.spy(mtx_a, marker='.', ms=4)
fig.tight_layout()
fig.savefig(inodir(get_figname('K-sparsity', options)),
bbox_inches='tight')
fig, ax = plt.subplots()
ax.spy(mtx_b, marker='.', ms=4)
fig.tight_layout()
fig.savefig(inodir(get_figname('M-sparsity', options)),
bbox_inches='tight')
if options.show:
plt.show()
if options.shell:
from sfepy.base.base import shell; shell()
if __name__ == '__main__':
main()