linear_elasticity/nodal_lcbcs.py

Description

Linear elasticity with nodal linear combination constraints.

Find such that:

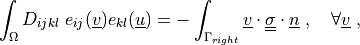
where

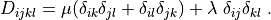
and 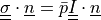with given traction pressure 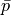. The constraints are given in terms of coefficient matrices and right-hand sides, see the lcbcs keyword below. For instance, 'nlcbc1' in the 3D mesh case corresponds to

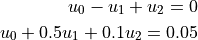
that should hold in the 'Top' region.

This example demonstrates how to pass command line options to a problem description file using --define option of sfepy-run. Try:

sfepy-run sfepy/examples/linear_elasticity/nodal_lcbcs.py --define='dim: 3'

to use a 3D mesh, instead of the default 2D mesh. The example also shows that the nodal constraints can be used in place of the Dirichlet boundary conditions. Try:

sfepy-run sfepy/examples/linear_elasticity/nodal_lcbcs.py --define='use_ebcs: False'

to replace ebcs with the 'nlcbc4' constraints. The results should be the same for the two cases. Both options can be combined:

sfepy-run sfepy/examples/linear_elasticity/nodal_lcbcs.py --define='dim: 3, use_ebcs: False'

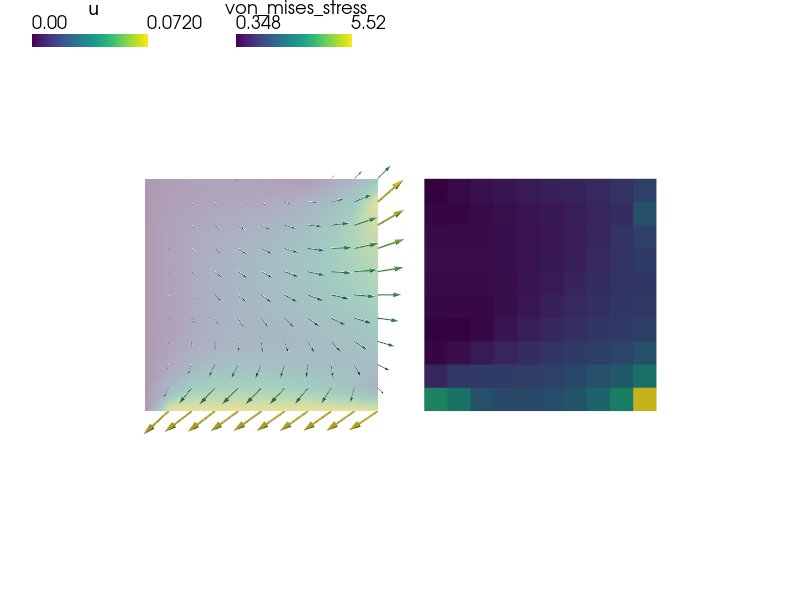
The post_process() function is used both to compute the von Mises stress and to verify the linear combination constraints.

View the 2D results using:

sfepy-view square_quad.vtk -2

View the 3D results using:

sfepy-view cube_medium_tetra.vtk

source code

r"""
Linear elasticity with nodal linear combination constraints.

Find :math:`\ul{u}` such that:

.. math::
    \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
    = - \int_{\Gamma_{right}} \ul{v} \cdot \ull{\sigma} \cdot \ul{n}
    \;, \quad \forall \ul{v} \;,

where

.. math::
    D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
    \lambda \ \delta_{ij} \delta_{kl}
    \;.

and :math:`\ull{\sigma} \cdot \ul{n} = \bar{p} \ull{I} \cdot \ul{n}` with given
traction pressure :math:`\bar{p}`. The constraints are given in terms of
coefficient matrices and right-hand sides, see the ``lcbcs`` keyword below. For
instance, ``'nlcbc1'`` in the 3D mesh case corresponds to

.. math::
    u_0 - u_1 + u_2 = 0 \\
    u_0 + 0.5 u_1 + 0.1 u_2 = 0.05

that should hold in the ``'Top'`` region.

This example demonstrates how to pass command line options to a problem
description file using ``--define`` option of ``sfepy-run``. Try::

  sfepy-run sfepy/examples/linear_elasticity/nodal_lcbcs.py --define='dim: 3'

to use a 3D mesh, instead of the default 2D mesh. The example also shows that
the nodal constraints can be used in place of the Dirichlet boundary
conditions. Try::

  sfepy-run sfepy/examples/linear_elasticity/nodal_lcbcs.py --define='use_ebcs: False'

to replace ``ebcs`` with the ``'nlcbc4'`` constraints. The results should be
the same for the two cases. Both options can be combined::

  sfepy-run sfepy/examples/linear_elasticity/nodal_lcbcs.py --define='dim: 3, use_ebcs: False'

The :func:`post_process()` function is used both to compute the von Mises
stress and to verify the linear combination constraints.

View the 2D results using::

  sfepy-view square_quad.vtk -2

View the 3D results using::

  sfepy-view cube_medium_tetra.vtk
"""
from __future__ import absolute_import
import numpy as nm

from sfepy.base.base import output, assert_
from sfepy.mechanics.matcoefs import stiffness_from_lame
from sfepy.mechanics.tensors import get_von_mises_stress
from sfepy import data_dir

def post_process(out, pb, state, extend=False):
    """
    Calculate and output strain and stress for given displacements.
    """
    from sfepy.base.base import Struct

    ev = pb.evaluate
    stress = ev('ev_cauchy_stress.2.Omega(m.D, u)', mode='el_avg')

    vms = get_von_mises_stress(stress.squeeze())
    vms.shape = (vms.shape[0], 1, 1, 1)
    out['von_mises_stress'] = Struct(name='output_data', mode='cell',
                                     data=vms, dofs=None)

    dim = pb.domain.shape.dim

    us = state().reshape((-1, dim))

    field = pb.fields['displacement']

    if dim == 2:
        ii = field.get_dofs_in_region(pb.domain.regions['Top'])
        output('top LCBC (u.0 - u.1 = 0):')
        output('\n', nm.c_[us[ii], nm.diff(us[ii], 1)])

        ii = field.get_dofs_in_region(pb.domain.regions['Bottom'])
        output('bottom LCBC (u.0 + u.1 = -0.1):')
        output('\n', nm.c_[us[ii], nm.sum(us[ii], 1)])

        ii = field.get_dofs_in_region(pb.domain.regions['Right'])
        output('right LCBC (u.0 + u.1 = linspace(0, 0.1)):')
        output('\n', nm.c_[us[ii], nm.sum(us[ii], 1)])

    else:
        ii = field.get_dofs_in_region(pb.domain.regions['Top'])
        output('top LCBC (u.0 - u.1 + u.2 = 0):')
        output('\n', nm.c_[us[ii], us[ii, 0] - us[ii, 1] + us[ii, 2]])
        output('top LCBC (u.0 + 0.5 u.1 + 0.1 u.2 = 0.05):')
        output('\n', nm.c_[us[ii],
                           us[ii, 0] + 0.5 * us[ii, 1] + 0.1 * us[ii, 2]])

        ii = field.get_dofs_in_region(pb.domain.regions['Bottom'])
        output('bottom LCBC (u.2 - 0.1 u.1 = 0.2):')
        output('\n', nm.c_[us[ii], us[ii, 2] - 0.1 * us[ii, 1]])

        ii = field.get_dofs_in_region(pb.domain.regions['Right'])
        output('right LCBC (u.0 + u.1 + u.2 = linspace(0, 0.1)):')
        output('\n', nm.c_[us[ii], nm.sum(us[ii], 1)])

    return out

def define(dim=2, use_ebcs=True):
    assert_(dim in (2, 3))

    if dim == 2:
        filename_mesh = data_dir + '/meshes/2d/square_quad.mesh'

    else:
        filename_mesh = data_dir + '/meshes/3d/cube_medium_tetra.mesh'

    options = {
        'nls' : 'newton',
        'ls' : 'ls',
        'post_process_hook' : 'post_process'
    }

    def get_constraints(ts, coors, region=None):
        mtx = nm.ones((coors.shape[0], 1, dim), dtype=nm.float64)

        rhs = nm.arange(coors.shape[0], dtype=nm.float64)[:, None]

        rhs *= 0.1 / (coors.shape[0] - 1)

        return mtx, rhs

    functions = {
        'get_constraints' : (get_constraints,),
    }

    fields = {
        'displacement': ('real', dim, 'Omega', 1),
    }

    materials = {
        'm' : ({
            'D' : stiffness_from_lame(dim, lam=5.769, mu=3.846),
        },),
        'load' : ({'val' : -1.0},),
    }

    variables = {
        'u' : ('unknown field', 'displacement', 0),
        'v' : ('test field', 'displacement', 'u'),
    }

    regions = {
        'Omega' : 'all',
        'Bottom' : ('vertices in (y < -0.499) -v r.Left', 'facet'),
        'Top' : ('vertices in (y > 0.499) -v r.Left', 'facet'),
        'Left' : ('vertices in (x < -0.499)', 'facet'),
        'Right' : ('vertices in (x > 0.499) -v (r.Bottom +v r.Top)', 'facet'),
    }

    if dim == 2:
        lcbcs = {
            'nlcbc1' : ('Top', {'u.all' : None}, None, 'nodal_combination',
                        ([[1.0, -1.0]], [0.0])),
            'nlcbc2' : ('Bottom', {'u.all' : None}, None, 'nodal_combination',
                        ([[1.0, 1.0]], [-0.1])),
            'nlcbc3' : ('Right', {'u.all' : None}, None, 'nodal_combination',
                        'get_constraints'),
        }

    else:
        lcbcs = {
            'nlcbc1' : ('Top', {'u.all' : None}, None, 'nodal_combination',
                        ([[1.0, -1.0, 1.0], [1.0, 0.5, 0.1]], [0.0, 0.05])),
            'nlcbc2' : ('Bottom', {'u.[2,1]' : None}, None, 'nodal_combination',
                        ([[1.0, -0.1]], [0.2])),
            'nlcbc3' : ('Right', {'u.all' : None}, None, 'nodal_combination',
                        'get_constraints'),
        }

    if use_ebcs:
        ebcs = {
            'fix' : ('Left', {'u.all' : 0.0}),
        }

    else:
        ebcs = {}

        lcbcs.update({
            'nlcbc4' : ('Left', {'u.all' : None}, None, 'nodal_combination',
                        (nm.eye(dim), nm.zeros(dim))),
        })

    equations = {
        'elasticity' : """
            dw_lin_elastic.2.Omega(m.D, v, u)
            = -dw_surface_ltr.2.Right(load.val, v)
        """,
    }

    solvers = {
        'ls' : ('ls.scipy_direct', {}),
        'newton' : ('nls.newton', {
            'i_max'      : 1,
            'eps_a'      : 1e-10,
        }),
    }

    return locals()