linear_elasticity/multi_point_constraints.py¶
Description
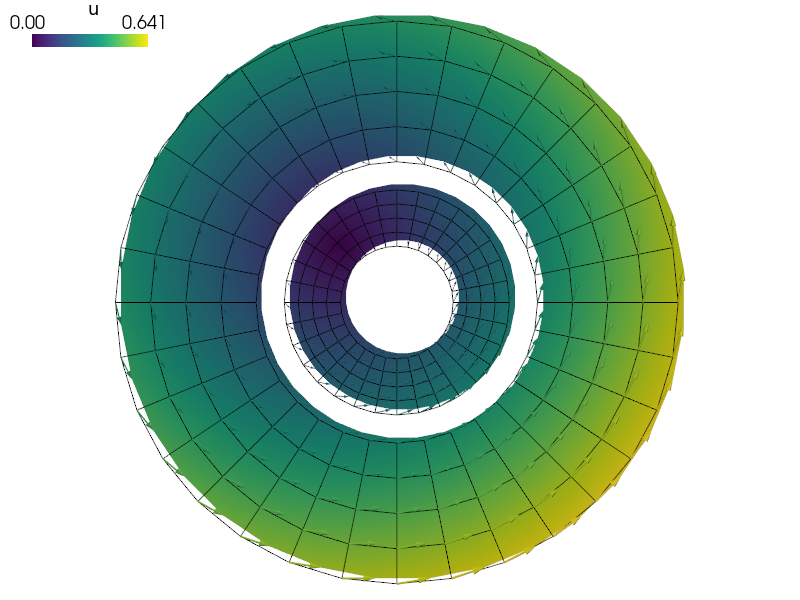
The linear elasticity of two discs connected using multi-point constraints.
Find 
, 
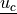such that:
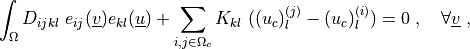
where
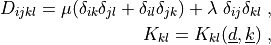
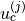are the DOFs - two displacements and one rotation in 2D -
of the node 
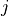in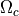 
, which is a subdomain composed of two
1D spring terms with the generalized stiffness matrix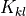 
depending
on the directions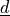 
of the springs and the stiffness vector
.
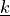The deformation is governed by the Dirichlet conditions applied to one of the
sping end points, see the dofs argument of define() below.
Usage Examples¶
Save and display boundary regions:
sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py --save-regions-as-groups --solve-not sfepy-view annulus-c_regions.vtk -2e -f Gamma1:p0 Gamma2:p1 Gamma3:p3 Gamma4:p4 --max-plots=4 --color-map=summer
Run:
sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py -d "dofs=(0,1)" sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py -d "dofs=2"
Display results:
sfepy-view annulus-c.vtk -2e sfepy-view annulus-c.vtk -2e -f u:wu:f1:p0 1:vw:p0 u:gu:p0
r"""
The linear elasticity of two discs connected using multi-point constraints.
Find :math:`\ul{u}`, :math:`\ul{u_c}` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
+ \sum_{i,j \in \Omega_c} K_{kl}\ ((u_c)^{(j)}_l - (u_c)^{(i)}_l)
= 0
\;, \quad \forall \ul{v} \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl} \;,
K_{kl} = K_{kl}(\ul{d}, \ul{k}) \;,
:math:`u_c^{(j)}` are the DOFs - two displacements and one rotation in 2D -
of the node :math:`j` in :math:`\Omega_c`, which is a subdomain composed of two
1D spring terms with the generalized stiffness matrix :math:`K_{kl}` depending
on the directions :math:`\ul{d}` of the springs and the stiffness vector
:math:`\ul{k}`.
The deformation is governed by the Dirichlet conditions applied to one of the
sping end points, see the `dofs` argument of :func:`define()` below.
Usage Examples
--------------
- Save and display boundary regions::
sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py --save-regions-as-groups --solve-not
sfepy-view annulus-c_regions.vtk -2e -f Gamma1:p0 Gamma2:p1 Gamma3:p3 Gamma4:p4 --max-plots=4 --color-map=summer
- Run::
sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py
sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py -d "dofs=(0,1)"
sfepy-run sfepy/examples/linear_elasticity/multi_point_constraints.py -d "dofs=2"
- Display results::
sfepy-view annulus-c.vtk -2e
sfepy-view annulus-c.vtk -2e -f u:wu:f1:p0 1:vw:p0 u:gu:p0
"""
import numpy as nm
from sfepy.mesh.mesh_generators import gen_cylinder_mesh
from sfepy.discrete.fem.meshio import UserMeshIO
from sfepy.discrete.fem.mesh import Mesh
from sfepy.linalg import get_coors_in_ball
from sfepy.mechanics.matcoefs import stiffness_from_lame
def define(dims=(1, 1, 2, 2, 0), shape=(5, 32, 0), order=1, dofs=(0, 1, 2),
is_rot=True, output_dir='.'):
if not isinstance(dofs, tuple):
dofs = (dofs,)
nuc = 2 + is_rot
dofs0 = tuple(set(range(nuc)).difference(dofs))
sdofs = ','.join([f'{ii}' for ii in dofs])
sdofs0 = ','.join([f'{ii}' for ii in dofs0])
def mesh_hook(mesh, mode):
if mode == 'read':
_mesh = gen_cylinder_mesh(dims, shape, (0, 0, 0),
make_2d=True)
_mesh2 = _mesh.copy()
_mesh2.transform_coors(nm.eye(2, dtype=nm.float64) * 2.5)
_mesh = _mesh + _mesh2
# Add constraint vertices (and cells) to the base mesh.
coors, vgroups, conns, mat_ids, descs = _mesh._get_io_data()
nc = coors.shape[0]
coors = nm.r_[coors, nm.zeros((4, 2), dtype=nm.float64)]
vgroups = nm.r_[vgroups, [1, 2, 3, 4]]
conns.append([[nc, nc + 1],
[nc + 2, nc + 3]])
mat_ids.append([1, 2])
descs.append('1_2')
mesh = Mesh.from_data('annulus-c',
coors, vgroups, conns, mat_ids, descs)
return mesh
elif mode == 'write':
pass
filename_mesh = UserMeshIO(mesh_hook)
regions = {
'Omega' : 'all',
'Gamma1' : ('vertices by get_gamma1', 'facet'),
'Gamma2' : ('vertices by get_gamma2', 'facet'),
'Gamma3' : ('vertices by get_gamma3', 'facet'),
'Gamma4' : ('vertices by get_gamma4', 'facet'),
'Omega12C' : ('(vertices of group 1) +v (vertices of group 2)',
'cell', None, {'cell_tdim': 1}),
'Gamma1C' : ('vertices of group 1', 'vertex'),
'Gamma2C' : ('vertices of group 2', 'vertex'),
'Omega34C' : ('(vertices of group 3) +v (vertices of group 4)',
'cell', None, {'cell_tdim': 1}),
'Gamma3C' : ('vertices of group 3', 'vertex'),
'Gamma4C' : ('vertices of group 4', 'vertex'),
'OmegaC' : ('r.Omega12C +c r.Omega34C', 'cell', None, {'cell_tdim': 1})
}
centre = [0, 0]
functions = {
'get_gamma1' : (lambda coors, domain:
get_coors_in_ball(coors, centre, 1.1, 0.9),),
'get_gamma2' : (lambda coors, domain:
get_coors_in_ball(coors, centre, 2.1, 1.9),),
'get_gamma3' : (lambda coors, domain:
get_coors_in_ball(coors, centre, 2.6, 2.4),),
'get_gamma4' : (lambda coors, domain:
get_coors_in_ball(coors, centre, 5.1, 4.9),),
}
fields = {
'fu' : ('real', 2, 'Omega', order),
'fc' : ('real', nuc, 'OmegaC', 1),
}
variables = {
'u' : ('unknown field', 'fu', 0),
'v' : ('test field', 'fu', 'u'),
'uc' : ('unknown field', 'fc', 1),
'vc' : ('test field', 'fc', 'uc'),
}
ebcs = {
'uc' : ('Gamma1C', {f'uc.[{sdofs}]' : 0.1},),
}
if dofs0:
ebcs.update({
'uc0' : ('Gamma1C', {f'uc.[{sdofs0}]' : 0.0},),
})
if not is_rot:
ebcs.update({
'u0' : ('Gamma4', {'u.all' : 0.0}),
})
lcbcs = {
'rigid' : (('Gamma1', 'Gamma2C'), {'u.all' : 'uc.all'},
None, 'rigid2'),
'avg1' : (('Gamma2', 'Gamma3C'), {'u.all' : 'uc.all'},
None, 'average_force'),
'avg2' : (('Gamma3', 'Gamma4C'), {'u.all' : 'uc.all'},
None, 'average_force'),
}
materials = {
'm' : ({
'D' : stiffness_from_lame(dim=2, lam=1e1, mu=1e0),
'ks' : [[1e+5], [1e+5], [1e+5]][:nuc],
'dvec' : [[0.01], [0.01]],
},),
}
integrals = {
'i' : 2 * order,
}
if is_rot:
equations = {
'eq1' :
"""dw_lin_elastic.i.Omega(m.D, v, u)
+ dw_lin_dspring_rot.0.Omega12C(m.dvec, m.ks, vc, uc)
+ dw_lin_dspring_rot.0.Omega34C(m.dvec, m.ks, vc, uc)
= 0
""",
}
else:
equations = {
'eq1' :
"""dw_lin_elastic.i.Omega(m.D, v, u)
+ dw_lin_dspring.0.Omega12C(m.dvec, m.ks, vc, uc)
+ dw_lin_dspring.0.Omega34C(m.dvec, m.ks, vc, uc)
= 0
""",
}
solvers = {
'ls' : ('ls.auto_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 1,
'eps_a' : -1e-10,
'check' : 0,
}),
}
options = {
'output_dir' : output_dir,
'nls' : 'newton',
'ls' : 'ls',
}
return locals()