linear_elasticity/prestress_fibres.py¶

Description

Linear elasticity with a given prestress in one subdomain and a (pre)strain fibre reinforcement in the other.

Find $\ul{u}$ such that:

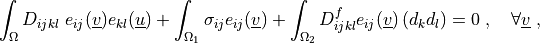
$\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u}) + \int_{\Omega_1} \sigma_{ij} e_{ij}(\ul{v}) + \int_{\Omega_2} D^f_{ijkl} e_{ij}(\ul{v}) \left(d_k d_l\right) = 0 \;, \quad \forall \ul{v} \;,$

where

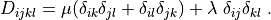
$D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) + \lambda \ \delta_{ij} \delta_{kl} \;.$

The stiffness of fibres 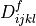$D^f_{ijkl}$ is defined analogously, 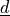$\ul{d}$ is the unit fibre direction vector and 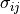$\sigma_{ij}$ is the prestress.

Visualization¶

Use the following to see the deformed structure with 10x magnified displacements:

sfepy-view block.vtk -f u:wu:f5 1:vw

../_images/linear_elasticity-prestress_fibres1.png

source code

r"""
Linear elasticity with a given prestress in one subdomain and a (pre)strain
fibre reinforcement in the other.

Find :math:`\ul{u}` such that:

.. math::
    \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
    + \int_{\Omega_1} \sigma_{ij} e_{ij}(\ul{v})
    + \int_{\Omega_2} D^f_{ijkl} e_{ij}(\ul{v}) \left(d_k d_l\right)
    = 0
    \;, \quad \forall \ul{v} \;,

where

.. math::
    D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
    \lambda \ \delta_{ij} \delta_{kl}
    \;.

The stiffness of fibres :math:`D^f_{ijkl}` is defined analogously,
:math:`\ul{d}` is the unit fibre direction vector and :math:`\sigma_{ij}` is
the prestress.

Visualization
-------------

Use the following to see the deformed structure with 10x magnified
displacements::

  sfepy-view block.vtk -f u:wu:f5 1:vw
"""
from __future__ import absolute_import
import numpy as nm
from sfepy.mechanics.matcoefs import stiffness_from_lame
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/3d/block.mesh'

regions = {
    'Omega' : 'all',
    'Left' : ('vertices in (x < -4.99)', 'facet'),
    'Omega1' : 'vertices in (x < 0.001)',
    'Omega2' : 'vertices in (x > -0.001)',
}

materials = {
    'solid' : ({
        'D' : stiffness_from_lame(3, lam=1e2, mu=1e1),
        'prestress' : 0.1 * nm.array([[1.0], [1.0], [1.0],
                                      [0.5], [0.5], [0.5]],
                                     dtype=nm.float64),
        'DF' : stiffness_from_lame(3, lam=8e0, mu=8e-1),
        'nu' : nm.array([[-0.5], [0.0], [0.5]], dtype=nm.float64),
    },),
}

fields = {
    'displacement': ('real', 'vector', 'Omega', 1),
}

variables = {
    'u' : ('unknown field', 'displacement', 0),
    'v' : ('test field', 'displacement', 'u'),
}

ebcs = {
    'Fixed' : ('Left', {'u.all' : 0.0}),
}

equations = {
    'balance_of_forces' :
    """dw_lin_elastic.2.Omega( solid.D, v, u )
     + dw_lin_prestress.2.Omega1( solid.prestress, v )
     + dw_lin_strain_fib.2.Omega2( solid.DF, solid.nu, v )
     = 0""",
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max' : 1,
        'eps_a' : 1e-10,
    }),
}