diffusion/poisson_nonlinear_material.py

Description

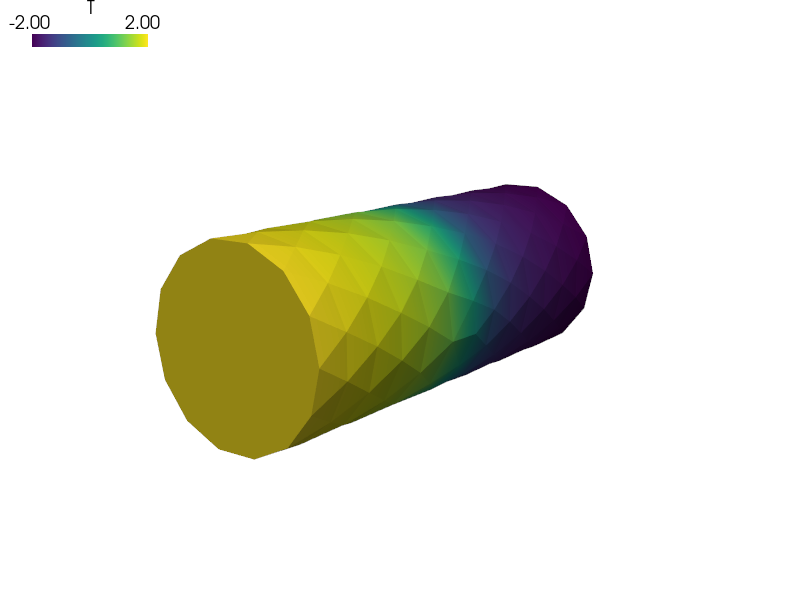
Nonlinear Poisson’s equation example demonstrating the nonlinear diffusion and nonlinear volume force terms.

The example is an adaptation of: diffusion/poisson_field_dependent_material.py.

Find 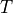such that:

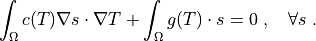
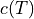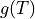where and are the 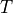dependent coefficients.

source code

r"""
Nonlinear Poisson's equation example demonstrating the nonlinear diffusion
and nonlinear volume force terms.

The example is an adaptation of:
:ref:`diffusion-poisson_field_dependent_material`.

Find :math:`T` such that:

.. math::
   \int_{\Omega} c(T) \nabla s \cdot \nabla T + \int_{\Omega} g(T) \cdot s
    = 0
    \;, \quad \forall s \;.

where :math:`c(T)` and :math:`g(T)`  are the :math:`T` dependent coefficients.
"""
from sfepy import data_dir
import numpy as np

filename_mesh = data_dir + '/meshes/3d/cylinder.mesh'

def get_conductivity(T):
    """
    Calculates the conductivity as (1 + T**4) and returns it.
    """
    val = 1 + T**4
    return val

def d_get_conductivity(T):
    """
    Calculates the derivative of get_conductivity and returns it.
    """
    val = 4*T**3
    return val

def nl_src(T):
    """
    Calculates a non linear source term as np.sinh(T) and returns it.
    """
    val = np.sinh(T)
    return val

def d_nl_src(T):
    """
    Calculates the derivative of the nl_src term and returns it.
    """
    val = np.cosh(T)
    return val

materials = {
}

fields = {
    'temperature' : ('real', 1, 'Omega', 1),
}

variables = {
    'T' : ('unknown field', 'temperature', 0),
    's' : ('test field',    'temperature', 'T'),
}

regions = {
    'Omega' : 'all',
    'Gamma_Left' : ('vertices in (x < 0.00001)', 'facet'),
    'Gamma_Right' : ('vertices in (x > 0.099999)', 'facet'),
}

ebcs = {
    'T1' : ('Gamma_Left', {'T.0' : 2.0}),
    'T2' : ('Gamma_Right', {'T.0' : -2.0}),
}

integrals = {
    'i' : 10,
}

equations = {
    'Temperature' : """
       dw_nl_diffusion.i.Omega(get_conductivity, d_get_conductivity, s, T)
     + dw_volume_nvf.i.Omega(nl_src, d_nl_src, s, T) = 0
     """
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max' : 15,
        'eps_a' : 1e-10,
        'eps_r' : 1.0,
        'ls_on' : 10,
    }),
}

options = {
    'nls' : 'newton',
    'ls' : 'ls',
    'save_times' : 'all',
}