diffusion/laplace_refine_interactive.py

Description

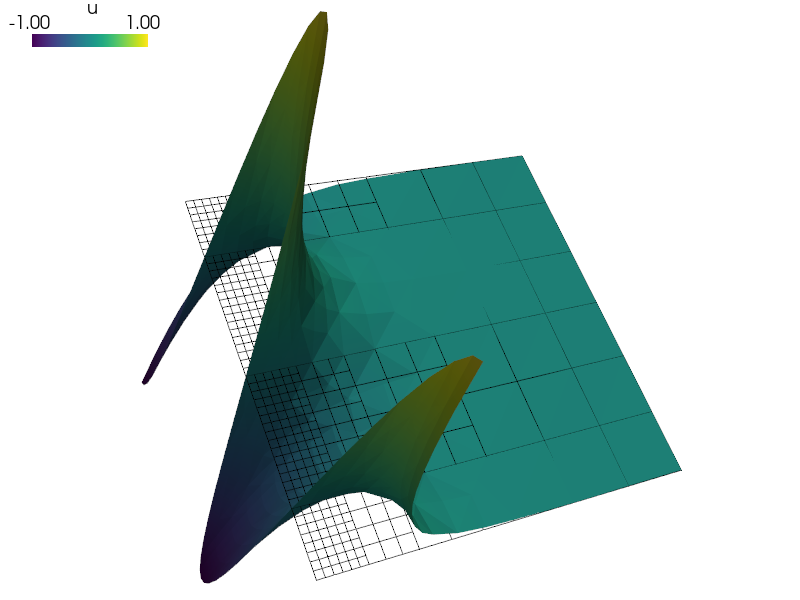
Example of solving Laplace’s equation on a block domain refined with level 1 hanging nodes.

The domain is progressively refined towards the edge/face of the block, where Dirichlet boundary conditions are prescribed by an oscillating function.

Find 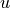such that:

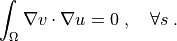
Notes

The implementation of the mesh refinement with level 1 hanging nodes is a proof-of-concept code with many unresolved issues. The main problem is the fact that a user needs to input the cells to refine at each level, while taking care of the following constraints:

• the level 1 hanging nodes constraint: a cell that has a less-refined neighbour cannot be refined;

• the implementation constraint: a cell with a refined neighbour cannot be refined.

The hanging nodes are treated by a basis transformation/DOF substitution, which has to be applied explicitly by the user:

• call field.substitute_dofs(subs) before assembling and solving;

• then call field.restore_dofs() before saving results.

Usage Examples

Default options, 2D, storing results in ‘output’ directory:

python3 sfepy/examples/diffusion/laplace_refine_interactive.py output
sfepy-view output/hanging.vtk -2 -f u:wu 1:vw

Default options, 3D, storing results in ‘output’ directory:

python3 sfepy/examples/diffusion/laplace_refine_interactive.py -3 output
sfepy-view output/hanging.vtk -f u:wu:f0.1 1:vw

Finer initial domain, 2D, storing results in ‘output’ directory:

python3 sfepy/examples/diffusion/laplace_refine_interactive.py --shape=11,11 output
sfepy-view output/hanging.vtk -2 -f u:wu 1:vw

Bi-quadratic approximation, 2D, storing results in ‘output’ directory:

python3 sfepy/examples/diffusion/laplace_refine_interactive.py --order=2 output

# View solution with higher order DOFs removed.
sfepy-view output/hanging.vtk -2 -f u:wu 1:vw

# View full solution on a mesh adapted for visualization.
sfepy-view output/hanging_u.vtk -2 -f u:wu 1:vw

source code

#!/usr/bin/env python
r"""
Example of solving Laplace's equation on a block domain refined with level 1
hanging nodes.

The domain is progressively refined towards the edge/face of the block, where
Dirichlet boundary conditions are prescribed by an oscillating function.

Find :math:`u` such that:

.. math::
    \int_{\Omega} \nabla v \cdot \nabla u = 0
    \;, \quad \forall s \;.

Notes
-----
The implementation of the mesh refinement with level 1 hanging nodes is a
proof-of-concept code with many unresolved issues. The main problem is the fact
that a user needs to input the cells to refine at each level, while taking care
of the following constraints:

- the level 1 hanging nodes constraint: a cell that has a less-refined
  neighbour cannot be refined;
- the implementation constraint: a cell with a refined neighbour cannot be
  refined.

The hanging nodes are treated by a basis transformation/DOF substitution, which
has to be applied explicitly by the user:

- call ``field.substitute_dofs(subs)`` before assembling and solving;
- then call ``field.restore_dofs()`` before saving results.

Usage Examples
--------------

Default options, 2D, storing results in 'output' directory::

  python3 sfepy/examples/diffusion/laplace_refine_interactive.py output
  sfepy-view output/hanging.vtk -2 -f u:wu 1:vw

Default options, 3D, storing results in 'output' directory::

  python3 sfepy/examples/diffusion/laplace_refine_interactive.py -3 output
  sfepy-view output/hanging.vtk -f u:wu:f0.1 1:vw


Finer initial domain, 2D, storing results in 'output' directory::

  python3 sfepy/examples/diffusion/laplace_refine_interactive.py --shape=11,11 output
  sfepy-view output/hanging.vtk -2 -f u:wu 1:vw

Bi-quadratic approximation, 2D, storing results in 'output' directory::

  python3 sfepy/examples/diffusion/laplace_refine_interactive.py --order=2 output

  # View solution with higher order DOFs removed.
  sfepy-view output/hanging.vtk -2 -f u:wu 1:vw

  # View full solution on a mesh adapted for visualization.
  sfepy-view output/hanging_u.vtk -2 -f u:wu 1:vw
"""
from __future__ import absolute_import
from argparse import RawDescriptionHelpFormatter, ArgumentParser

import os
import sys
sys.path.append('.')
import numpy as nm

from sfepy.base.base import output, Struct
from sfepy.base.ioutils import ensure_path
from sfepy.mesh.mesh_generators import gen_block_mesh
from sfepy.discrete import (FieldVariable, Integral, Equation, Equations,
                            Function, Problem)
from sfepy.discrete.fem import FEDomain, Field
from sfepy.discrete.conditions import (Conditions, EssentialBC)
import sfepy.discrete.fem.refine_hanging as rh
from sfepy.solvers.ls import ScipyDirect
from sfepy.solvers.nls import Newton
from sfepy.terms import Term

def refine_towards_facet(domain0, grading, axis):
    subs = None
    domain = domain0
    for level, coor in enumerate(grading):
        refine = nm.zeros(domain.mesh.n_el, dtype=nm.uint8)

        region = domain.create_region('aux',
                                      'vertices in (%s %.10f)' % (axis, coor),
                                      add_to_regions=False)
        refine[region.cells] = 1

        domain, subs = rh.refine(domain, refine, subs=subs)

    return domain, subs

helps = {
    'output_dir' :
    'output directory',
    'dims' :
    'dimensions of the block [default: %(default)s]',
    'shape' :
    'shape (counts of nodes in x, y[, z]) of the block [default: %(default)s]',
    'centre' :
    'centre of the block [default: %(default)s]',
    '3d' :
    'generate a 3D block',
    'order' :
    'field approximation order',
}

def main():
    parser = ArgumentParser(description=__doc__.rstrip(),
                            formatter_class=RawDescriptionHelpFormatter)
    parser.add_argument('output_dir', help=helps['output_dir'])
    parser.add_argument('--dims', metavar='dims',
                        action='store', dest='dims',
                        default='1.0,1.0,1.0', help=helps['dims'])
    parser.add_argument('--shape', metavar='shape',
                        action='store', dest='shape',
                        default='7,7,7', help=helps['shape'])
    parser.add_argument('--centre', metavar='centre',
                        action='store', dest='centre',
                        default='0.0,0.0,0.0', help=helps['centre'])
    parser.add_argument('-3', '--3d',
                        action='store_true', dest='is_3d',
                        default=False, help=helps['3d'])
    parser.add_argument('--order', metavar='int', type=int,
                        action='store', dest='order',
                        default=1, help=helps['order'])
    options = parser.parse_args()

    dim = 3 if options.is_3d else 2
    dims = nm.array(eval(options.dims), dtype=nm.float64)[:dim]
    shape = nm.array(eval(options.shape), dtype=nm.int32)[:dim]
    centre = nm.array(eval(options.centre), dtype=nm.float64)[:dim]

    output('dimensions:', dims)
    output('shape:     ', shape)
    output('centre:    ', centre)

    mesh0 = gen_block_mesh(dims, shape, centre, name='block-fem',
                           verbose=True)
    domain0 = FEDomain('d', mesh0)

    bbox = domain0.get_mesh_bounding_box()
    min_x, max_x = bbox[:, 0]
    eps = 1e-8 * (max_x - min_x)

    cnt = (shape[0] - 1) // 2
    g0 = 0.5 * dims[0]
    grading = nm.array([g0 / 2**ii for ii in range(cnt)]) + eps + centre[0] - g0

    domain, subs = refine_towards_facet(domain0, grading, 'x <')

    omega = domain.create_region('Omega', 'all')

    gamma1 = domain.create_region('Gamma1',
                                  'vertices in (x < %.10f)' % (min_x + eps),
                                  'facet')
    gamma2 = domain.create_region('Gamma2',
                                  'vertices in (x > %.10f)' % (max_x - eps),
                                  'facet')

    field = Field.from_args('fu', nm.float64, 1, omega,
                            approx_order=options.order)

    if subs is not None:
        field.substitute_dofs(subs)

    u = FieldVariable('u', 'unknown', field)
    v = FieldVariable('v', 'test', field, primary_var_name='u')

    integral = Integral('i', order=2*options.order)

    t1 = Term.new('dw_laplace(v, u)',
                  integral, omega, v=v, u=u)
    eq = Equation('eq', t1)
    eqs = Equations([eq])

    def u_fun(ts, coors, bc=None, problem=None):
        """
        Define a displacement depending on the y coordinate.
        """
        if coors.shape[1] == 2:
            min_y, max_y = bbox[:, 1]
            y = (coors[:, 1] - min_y) / (max_y - min_y)

            val = (max_y - min_y) * nm.cos(3 * nm.pi * y)

        else:
            min_y, max_y = bbox[:, 1]
            min_z, max_z = bbox[:, 2]
            y = (coors[:, 1] - min_y) / (max_y - min_y)
            z = (coors[:, 2] - min_z) / (max_z - min_z)

            val = ((max_y - min_y) * (max_z - min_z)
                   * nm.cos(3 * nm.pi * y) * (1.0 + 3.0 * (z - 0.5)**2))

        return val

    bc_fun = Function('u_fun', u_fun)
    fix1 = EssentialBC('shift_u', gamma1, {'u.0' : bc_fun})
    fix2 = EssentialBC('fix2', gamma2, {'u.all' : 0.0})

    ls = ScipyDirect({})

    nls = Newton({}, lin_solver=ls)

    pb = Problem('heat', equations=eqs)

    pb.set_bcs(ebcs=Conditions([fix1, fix2]))

    pb.set_solver(nls)

    state = pb.solve(save_results=False)

    if subs is not None:
        field.restore_dofs()

    filename = os.path.join(options.output_dir, 'hanging.vtk')
    ensure_path(filename)

    pb.save_state(filename, state)
    if options.order > 1:
        pb.save_state(filename, state, linearization=Struct(kind='adaptive',
                                                            min_level=0,
                                                            max_level=8,
                                                            eps=1e-3))

if __name__ == '__main__':
    main()