diffusion/laplace_shifted_periodic.py

Description

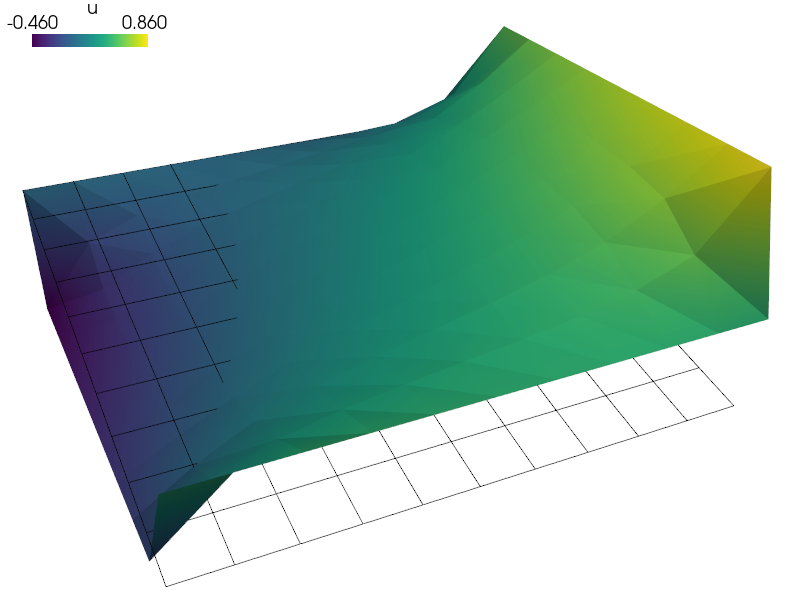
Laplace equation with shifted periodic BCs.

Display using:

sfepy-view laplace_shifted_periodic.vtk -f u:wu:f0.5 1:vw

source code

#!/usr/bin/env python
"""
Laplace equation with shifted periodic BCs.

Display using::

  sfepy-view laplace_shifted_periodic.vtk -f u:wu:f0.5 1:vw
"""
from __future__ import absolute_import
import sys
sys.path.append('.')
from argparse import ArgumentParser, RawDescriptionHelpFormatter
import numpy as nm

from sfepy.base.base import output
from sfepy.discrete import (FieldVariable, Integral, Equation, Equations,
                            Function, Problem)
from sfepy.discrete.fem import FEDomain, Field
from sfepy.terms import Term
from sfepy.discrete.conditions import (Conditions, EssentialBC,
                                       LinearCombinationBC)
from sfepy.solvers.ls import ScipyDirect
from sfepy.solvers.nls import Newton
from sfepy.mesh.mesh_generators import gen_block_mesh
import sfepy.discrete.fem.periodic as per

def run(domain, order, output_dir=''):
    omega = domain.create_region('Omega', 'all')
    bbox = domain.get_mesh_bounding_box()
    min_x, max_x = bbox[:, 0]
    min_y, max_y = bbox[:, 1]
    eps = 1e-8 * (max_x - min_x)
    gamma1 = domain.create_region('Gamma1',
                                  'vertices in (x < %.10f)' % (min_x + eps),
                                  'facet')
    gamma2 = domain.create_region('Gamma2',
                                  'vertices in (x > %.10f)' % (max_x - eps),
                                  'facet')
    gamma3 = domain.create_region('Gamma3',
                                  'vertices in y < %.10f' % (min_y + eps),
                                  'facet')
    gamma4 = domain.create_region('Gamma4',
                                  'vertices in y > %.10f' % (max_y - eps),
                                  'facet')

    field = Field.from_args('fu', nm.float64, 1, omega, approx_order=order)

    u = FieldVariable('u', 'unknown', field)
    v = FieldVariable('v', 'test', field, primary_var_name='u')

    integral = Integral('i', order=2*order)

    t1 = Term.new('dw_laplace(v, u)',
                  integral, omega, v=v, u=u)
    eq = Equation('eq', t1)
    eqs = Equations([eq])

    fix1 = EssentialBC('fix1', gamma1, {'u.0' : 0.4})
    fix2 = EssentialBC('fix2', gamma2, {'u.0' : 0.0})

    def get_shift(ts, coors, region):
        return nm.ones_like(coors[:, 0])

    dof_map_fun = Function('dof_map_fun', per.match_x_line)
    shift_fun = Function('shift_fun', get_shift)

    sper = LinearCombinationBC('sper', [gamma3, gamma4], {'u.0' : 'u.0'},
                               dof_map_fun, 'shifted_periodic',
                               arguments=(shift_fun,))

    ls = ScipyDirect({})
    nls = Newton({}, lin_solver=ls)

    pb = Problem('laplace', equations=eqs)
    pb.set_output_dir(output_dir)

    pb.set_bcs(ebcs=Conditions([fix1, fix2]), lcbcs=Conditions([sper]))

    pb.set_solver(nls)

    state = pb.solve()

    return pb, state

helps = {
    'dims' :
    'dimensions of the block [default: %(default)s]',
    'centre' :
    'centre of the block [default: %(default)s]',
    'shape' :
    'numbers of vertices along each axis [default: %(default)s]',
}

def main():
    parser = ArgumentParser(description=__doc__,
                            formatter_class=RawDescriptionHelpFormatter)
    parser.add_argument('--version', action='version', version='%(prog)s')
    parser.add_argument('-d', '--dims', metavar='dims',
                        action='store', dest='dims',
                        default='[1.0, 1.0]', help=helps['dims'])
    parser.add_argument('-c', '--centre', metavar='centre',
                        action='store', dest='centre',
                        default='[0.0, 0.0]', help=helps['centre'])
    parser.add_argument('-s', '--shape', metavar='shape',
                        action='store', dest='shape',
                        default='[11, 11]', help=helps['shape'])
    options = parser.parse_args()

    dims = nm.array(eval(options.dims), dtype=nm.float64)
    centre = nm.array(eval(options.centre), dtype=nm.float64)
    shape = nm.array(eval(options.shape), dtype=nm.int32)

    output('dimensions:', dims)
    output('centre:    ', centre)
    output('shape:     ', shape)

    mesh = gen_block_mesh(dims, shape, centre, name='block-fem')
    fe_domain = FEDomain('domain', mesh)

    pb, state = run(fe_domain, 1)
    pb.save_state('laplace_shifted_periodic.vtk', state)


if __name__ == '__main__':
    main()