multi_physics/thermal_electric.py

Description

First solve the stationary electric conduction problem. Then use its results to solve the evolutionary heat conduction problem.

Run this example as on a command line:

$ python <path_to_this_file>/thermal_electric.py

source code

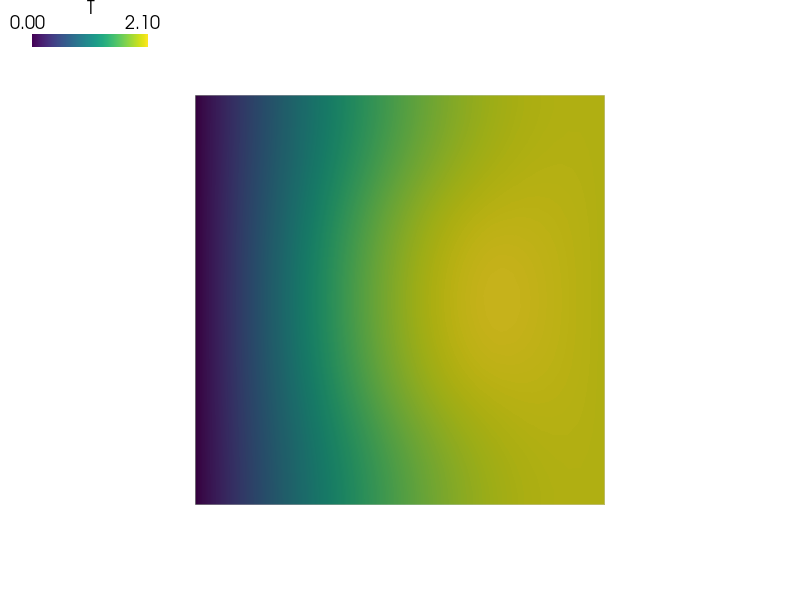
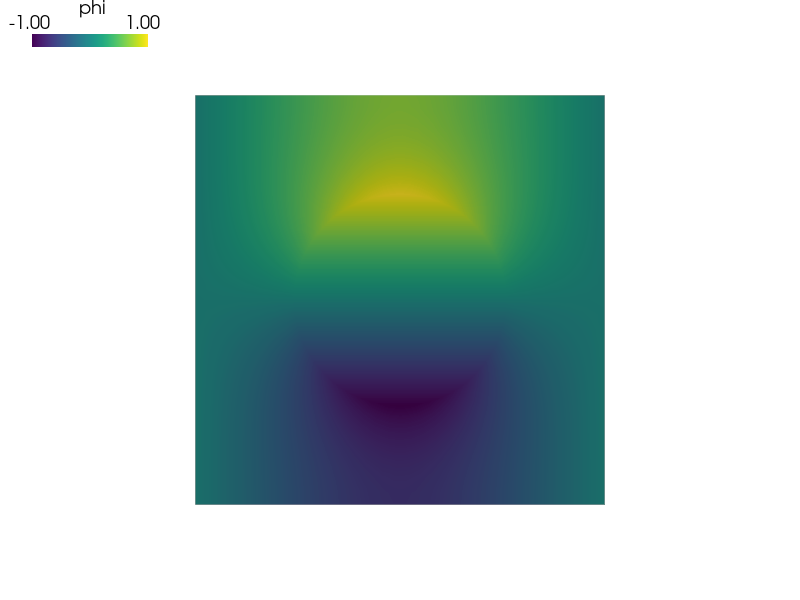
#!/usr/bin/env python
"""
First solve the stationary electric conduction problem. Then use its
results to solve the evolutionary heat conduction problem.

Run this example as on a command line::

    $ python <path_to_this_file>/thermal_electric.py
"""
from __future__ import absolute_import
import sys
sys.path.append( '.' )
import os

from sfepy import data_dir

filename_mesh = data_dir + '/meshes/2d/special/circle_in_square.mesh'

# Time stepping for the heat conduction problem.
t0 = 0.0
t1 = 0.5
n_step = 11

# Material parameters.
specific_heat = 1.2

##########

cwd = os.path.split(os.path.join(os.getcwd(), __file__))[0]

options = {
    'absolute_mesh_path' : True,
    'output_dir' : os.path.join(cwd, 'output')
}

regions = {
    'Omega' : 'all',
    'Omega1' : 'cells of group 1',
    'Omega2' : 'cells of group 2',
    'Omega2_Surface': ('r.Omega1 *v r.Omega2', 'facet'),
    'Left' : ('vertices in (x < %f)' % -0.4999, 'facet'),
    'Right' : ('vertices in (x > %f)' % 0.4999, 'facet'),
}

materials = {
    'm' : ({
        'thermal_conductivity' : 2.0,
        'electric_conductivity' : 1.5,
    },),
}

# The fields use the same approximation, so a single field could be used
# instead.
fields = {
    'temperature': ('real', 1, 'Omega', 1),
    'potential' : ('real', 1, 'Omega', 1),
}

variables = {
    'T' : ('unknown field', 'temperature', 0, 1),
    's' : ('test field', 'temperature', 'T'),
    'phi' : ('unknown field', 'potential', 1),
    'psi' : ('test field', 'potential', 'phi'),
    'phi_known' : ('parameter field', 'potential', '(set-to-None)'),
}

ics = {
    'ic' : ('Omega', {'T.0' : 0.0}),
}

ebcs = {
    'left' : ('Left', {'T.0' : 0.0, 'phi.0' : 0.0}),
    'right' : ('Right', {'T.0' : 2.0, 'phi.0' : 0.0}),
    'inside' : ('Omega2_Surface', {'phi.0' : 'set_electric_bc'}),
}

def set_electric_bc(coor):
    y = coor[:,1]
    ymin, ymax = y.min(), y.max()
    val = 2.0 * (((y - ymin) / (ymax - ymin)) - 0.5)
    return val

functions = {
    'set_electric_bc' : (lambda ts, coor, bc, problem, **kwargs:
                         set_electric_bc(coor),),
}

equations = {
    '2' : """%.12e * dw_dot.2.Omega( s, dT/dt )
             + dw_laplace.2.Omega( m.thermal_conductivity, s, T )
             = dw_electric_source.2.Omega( m.electric_conductivity,
                                           s, phi_known ) """ % specific_heat,
    '1' : """dw_laplace.2.Omega( m.electric_conductivity, psi, phi ) = 0""",
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max'      : 1,
        'eps_a'      : 1e-10,
        'problem'   : 'nonlinear',
    }),
    'ts' : ('ts.simple', {
        't0'     : t0,
        't1'     : t1,
        'dt'     : None,
        'n_step' : n_step, # has precedence over dt!
        'verbose' : 1,
    }),
}

def main():
    from sfepy.base.base import output
    from sfepy.base.conf import ProblemConf, get_standard_keywords
    from sfepy.discrete import Problem

    output.prefix = 'therel:'

    required, other = get_standard_keywords()
    conf = ProblemConf.from_file(__file__, required, other)

    problem = Problem.from_conf(conf, init_equations=False)

    # Setup output directory according to options above.
    problem.setup_default_output()

    # First solve the stationary electric conduction problem.
    problem.set_equations({'eq' : conf.equations['1']})
    state_el = problem.solve()
    problem.save_state(problem.get_output_name(suffix = 'el'), state_el)

    # Then solve the evolutionary heat conduction problem, using state_el.
    problem.set_equations({'eq' : conf.equations['2']})
    phi_var = problem.get_variables()['phi_known']
    phi_var.set_data(state_el())
    problem.solve()

    output('results saved in %s' % problem.get_output_name(suffix = '*'))

if __name__ == '__main__':
    main()