multi_physics/biot_npbc.py¶
Description
Biot problem - deformable porous medium with the no-penetration boundary condition on a boundary region.
Find  ,
,  such that:
such that:
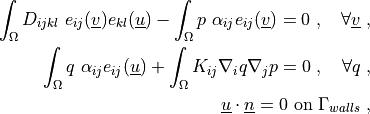
where
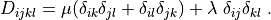

r"""
Biot problem - deformable porous medium with the no-penetration boundary
condition on a boundary region.
Find :math:`\ul{u}`, :math:`p` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
- \int_{\Omega} p\ \alpha_{ij} e_{ij}(\ul{v})
= 0
\;, \quad \forall \ul{v} \;,
\int_{\Omega} q\ \alpha_{ij} e_{ij}(\ul{u})
+ \int_{\Omega} K_{ij} \nabla_i q \nabla_j p
= 0
\;, \quad \forall q \;,
\ul{u} \cdot \ul{n} = 0 \mbox{ on } \Gamma_{walls} \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
"""
import os
import numpy as nm
from sfepy.linalg import get_coors_in_tube
from sfepy.mechanics.matcoefs import stiffness_from_lame
def define():
from sfepy import data_dir
filename = data_dir + '/meshes/3d/cylinder.mesh'
output_dir = 'output'
return define_input(filename, output_dir)
def cinc_simple(coors, mode):
axis = nm.array([1, 0, 0], nm.float64)
if mode == 0: # In
centre = nm.array([0.0, 0.0, 0.0], nm.float64)
radius = 0.019
length = 0.00002
elif mode == 1: # Out
centre = nm.array([0.1, 0.0, 0.0], nm.float64)
radius = 0.019
length = 0.00002
elif mode == 2: # Rigid
centre = nm.array([0.05, 0.0, 0.0], nm.float64)
radius = 0.015
length = 0.03
else:
raise ValueError('unknown mode %s!' % mode)
return get_coors_in_tube(coors,
centre, axis, -1, radius, length)
def define_regions(filename):
if filename.find('simple.mesh'):
dim = 3
regions = {
'Omega' : 'all',
'Walls' : ('vertices of surface -v (r.Outlet +f r.Inlet)', 'facet'),
'Inlet' : ('vertices by cinc_simple0', 'facet'),
'Outlet' : ('vertices by cinc_simple1', 'facet'),
'Rigid' : 'vertices by cinc_simple2',
}
else:
raise ValueError('unknown mesh %s!' % filename)
return regions, dim
def get_pars(ts, coor, mode, output_dir='.', **kwargs):
if mode == 'qp':
n_nod, dim = coor.shape
sym = (dim + 1) * dim // 2
out = {}
out['D'] = nm.tile(stiffness_from_lame(dim, lam=1.7, mu=0.3),
(coor.shape[0], 1, 1))
aa = nm.zeros((sym, 1), dtype=nm.float64)
aa[:dim] = 0.132
aa[dim:sym] = 0.092
out['alpha'] = nm.tile(aa, (coor.shape[0], 1, 1))
perm = nm.eye(dim, dtype=nm.float64)
out['K'] = nm.tile(perm, (coor.shape[0], 1, 1))
return out
def post_process(out, pb, state, extend=False):
from sfepy.base.base import Struct
dvel = pb.evaluate('ev_diffusion_velocity.i.Omega( m.K, p )',
mode='el_avg')
out['dvel'] = Struct(name='output_data',
mode='cell', data=dvel, dofs=None)
stress = pb.evaluate('ev_cauchy_stress.i.Omega( m.D, u )',
mode='el_avg')
out['cauchy_stress'] = Struct(name='output_data',
mode='cell', data=stress, dofs=None)
return out
def define_input(filename, output_dir):
filename_mesh = filename
options = {
'output_dir' : output_dir,
'output_format' : 'vtk',
'post_process_hook' : 'post_process',
'ls' : 'ls',
'nls' : 'newton',
}
functions = {
'cinc_simple0' : (lambda coors, domain:
cinc_simple(coors, 0),),
'cinc_simple1' : (lambda coors, domain:
cinc_simple(coors, 1),),
'cinc_simple2' : (lambda coors, domain:
cinc_simple(coors, 2),),
'get_pars' : (lambda ts, coors, mode=None, **kwargs:
get_pars(ts, coors, mode,
output_dir=output_dir, **kwargs),),
}
regions, dim = define_regions(filename_mesh)
field_1 = {
'name' : 'displacement',
'dtype' : nm.float64,
'shape' : dim,
'region' : 'Omega',
'approx_order' : 1,
}
field_2 = {
'name' : 'pressure',
'dtype' : nm.float64,
'shape' : 1,
'region' : 'Omega',
'approx_order' : 1,
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
'p' : ('unknown field', 'pressure', 1),
'q' : ('test field', 'pressure', 'p'),
}
ebcs = {
'inlet' : ('Inlet', {'p.0' : 1.0, 'u.all' : 0.0}),
'outlet' : ('Outlet', {'p.0' : -1.0}),
}
lcbcs = {
'rigid' : ('Outlet', {'u.all' : None}, None, 'rigid'),
'no_penetration' : ('Walls', {'u.all' : None}, None,
'no_penetration', None),
}
material_1 = {
'name' : 'm',
'function' : 'get_pars',
}
integral_1 = {
'name' : 'i',
'order' : 2,
}
equations = {
'eq_1' :
"""dw_lin_elastic.i.Omega( m.D, v, u )
- dw_biot.i.Omega( m.alpha, v, p )
= 0""",
'eq_2' :
"""dw_biot.i.Omega( m.alpha, u, q )
+ dw_diffusion.i.Omega( m.K, q, p )
= 0""",
}
solver_0 = {
'name' : 'ls',
'kind' : 'ls.scipy_direct', # Direct solver.
}
solver_1 = {
'name' : 'newton',
'kind' : 'nls.newton',
}
return locals()