multi_physics/biot.py¶
Description
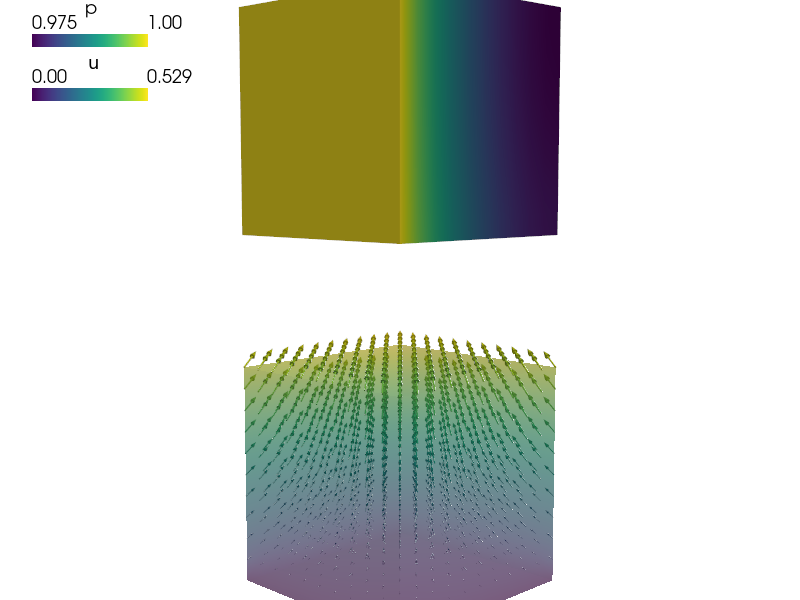
Biot problem - deformable porous medium.
Find  ,
,  such that:
such that:
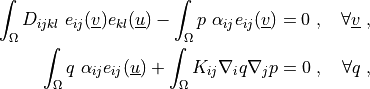
where
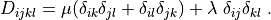
r"""
Biot problem - deformable porous medium.
Find :math:`\ul{u}`, :math:`p` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
- \int_{\Omega} p\ \alpha_{ij} e_{ij}(\ul{v})
= 0
\;, \quad \forall \ul{v} \;,
\int_{\Omega} q\ \alpha_{ij} e_{ij}(\ul{u})
+ \int_{\Omega} K_{ij} \nabla_i q \nabla_j p
= 0
\;, \quad \forall q \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
"""
import numpy as nm
from sfepy import data_dir
from sfepy.mechanics.matcoefs import stiffness_from_lame
filename_mesh = data_dir + '/meshes/3d/cube_medium_hexa.mesh'
regions = {
'Omega' : 'all',
'Bottom' : ('vertices in (z < -0.4999999)', 'facet'),
'Top' : ('vertices in (z > 0.4999999)', 'facet'),
'Left' : ('vertices in (x < -0.4999999)', 'facet'),
}
field_1 = {
'name' : 'displacement',
'dtype' : nm.float64,
'shape' : (3,),
'region' : 'Omega',
'approx_order' : 1,
}
field_2 = {
'name' : 'pressure',
'dtype' : nm.float64,
'shape' : (1,),
'region' : 'Omega',
'approx_order' : 1,
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
'p' : ('unknown field', 'pressure', 1),
'q' : ('test field', 'pressure', 'p'),
}
ebcs = {
'fix_u' : ('Bottom', {'u.all' : 0.0}),
'load_u' : ('Top', {'u.2' : 0.2}),
'load_p' : ('Left', {'p.all' : 1.0}),
}
material_1 = {
'name' : 'm',
'values' : {
'D': stiffness_from_lame(dim=3, lam=1.7, mu=0.3),
'alpha' : nm.array( [[0.132], [0.132], [0.132],
[0.092], [0.092], [0.092]],
dtype = nm.float64 ),
'K' : nm.array( [[2.0, 0.2, 0.0], [0.2, 1.0, 0.0], [0.0, 0.0, 0.5]],
dtype = nm.float64 ),
}
}
integral_1 = {
'name' : 'i1',
'order' : 1,
}
integral_2 = {
'name' : 'i2',
'order' : 2,
}
equations = {
'eq_1' :
"""dw_lin_elastic.i2.Omega( m.D, v, u )
- dw_biot.i1.Omega( m.alpha, v, p )
= 0""",
'eq_2' :
"""dw_biot.i1.Omega( m.alpha, u, q ) + dw_diffusion.i1.Omega( m.K, q, p )
= 0""",
}
solver_0 = {
'name' : 'ls_d',
'kind' : 'ls.scipy_direct',
}
solver_1 = {
'name' : 'newton',
'kind' : 'nls.newton',
'i_max' : 1,
'eps_a' : 1e-10,
'eps_r' : 1.0,
'macheps' : 1e-16,
'lin_red' : 1e-2, # Linear system error < (eps_a * lin_red).
'ls_red' : 0.1,
'ls_red_warp' : 0.001,
'ls_on' : 1.1,
'ls_min' : 1e-5,
'check' : 0,
'delta' : 1e-6,
}