linear_elasticity/its2D_interactive.py¶
Description
Diametrically point loaded 2-D disk, using commands for interactive use. See Primer.
The script combines the functionality of all the its2D_?.py examples and
allows setting various simulation parameters, namely:
material parameters
displacement field approximation order
uniform mesh refinement level
The example shows also how to probe the results as in
linear_elasticity/its2D_4.py. Using sfepy.discrete.probes allows
correct probing of fields with the approximation order greater than one.
In the SfePy top-level directory the following command can be used to get usage information:
python sfepy/examples/linear_elasticity/its2D_interactive.py -h
#!/usr/bin/env python
"""
Diametrically point loaded 2-D disk, using commands for interactive use. See
:ref:`sec-primer`.
The script combines the functionality of all the ``its2D_?.py`` examples and
allows setting various simulation parameters, namely:
- material parameters
- displacement field approximation order
- uniform mesh refinement level
The example shows also how to probe the results as in
:ref:`linear_elasticity-its2D_4`. Using :mod:`sfepy.discrete.probes` allows
correct probing of fields with the approximation order greater than one.
In the SfePy top-level directory the following command can be used to get usage
information::
python sfepy/examples/linear_elasticity/its2D_interactive.py -h
"""
import sys
sys.path.append('.')
from argparse import ArgumentParser, RawDescriptionHelpFormatter
import numpy as nm
import matplotlib.pyplot as plt
from sfepy.base.base import assert_, output, ordered_iteritems, IndexedStruct
from sfepy.discrete import (FieldVariable, Material, Integral, Integrals,
Equation, Equations, Problem)
from sfepy.discrete.fem import Mesh, FEDomain, Field
from sfepy.terms import Term
from sfepy.discrete.conditions import Conditions, EssentialBC
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy.solvers.auto_fallback import AutoDirect
from sfepy.solvers.nls import Newton
from sfepy.discrete.fem.geometry_element import geometry_data
from sfepy.discrete.probes import LineProbe
from sfepy.discrete.projections import project_by_component
from sfepy.examples.linear_elasticity.its2D_2 import stress_strain
from sfepy.examples.linear_elasticity.its2D_3 import nodal_stress
def gen_lines(problem):
"""
Define two line probes.
Additional probes can be added by appending to `ps0` (start points) and
`ps1` (end points) lists.
"""
ps0 = [[0.0, 0.0], [0.0, 0.0]]
ps1 = [[75.0, 0.0], [0.0, 75.0]]
# Use enough points for higher order approximations.
n_point = 1000
labels = ['%s -> %s' % (p0, p1) for p0, p1 in zip(ps0, ps1)]
probes = []
for ip in range(len(ps0)):
p0, p1 = ps0[ip], ps1[ip]
probes.append(LineProbe(p0, p1, n_point))
return probes, labels
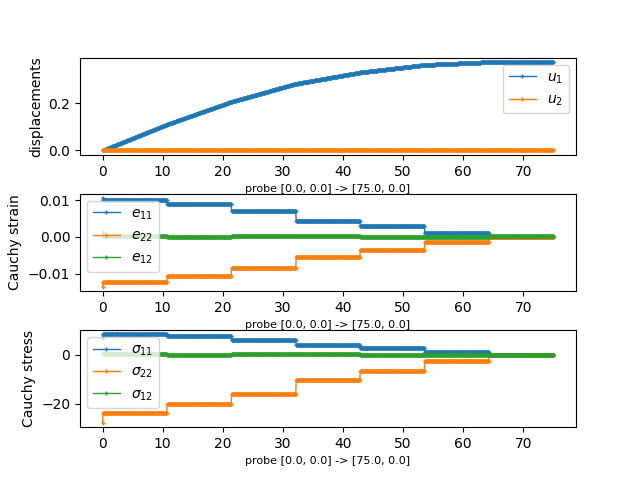
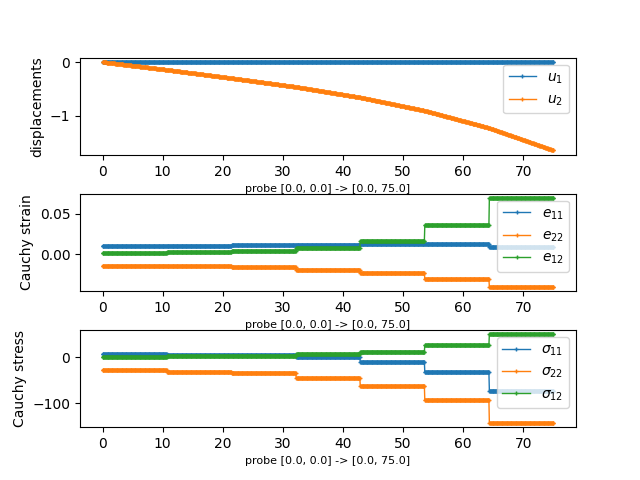
def probe_results(u, strain, stress, probe, label):
"""
Probe the results using the given probe and plot the probed values.
"""
results = {}
pars, vals = probe(u)
results['u'] = (pars, vals)
pars, vals = probe(strain)
results['cauchy_strain'] = (pars, vals)
pars, vals = probe(stress)
results['cauchy_stress'] = (pars, vals)
fig = plt.figure()
plt.clf()
fig.subplots_adjust(hspace=0.4)
plt.subplot(311)
pars, vals = results['u']
for ic in range(vals.shape[1]):
plt.plot(pars, vals[:,ic], label=r'$u_{%d}$' % (ic + 1),
lw=1, ls='-', marker='+', ms=3)
plt.ylabel('displacements')
plt.xlabel('probe %s' % label, fontsize=8)
plt.legend(loc='best', fontsize=10)
sym_indices = ['11', '22', '12']
plt.subplot(312)
pars, vals = results['cauchy_strain']
for ic in range(vals.shape[1]):
plt.plot(pars, vals[:,ic], label=r'$e_{%s}$' % sym_indices[ic],
lw=1, ls='-', marker='+', ms=3)
plt.ylabel('Cauchy strain')
plt.xlabel('probe %s' % label, fontsize=8)
plt.legend(loc='best', fontsize=10)
plt.subplot(313)
pars, vals = results['cauchy_stress']
for ic in range(vals.shape[1]):
plt.plot(pars, vals[:,ic], label=r'$\sigma_{%s}$' % sym_indices[ic],
lw=1, ls='-', marker='+', ms=3)
plt.ylabel('Cauchy stress')
plt.xlabel('probe %s' % label, fontsize=8)
plt.legend(loc='best', fontsize=10)
return fig, results
helps = {
'young' : "the Young's modulus [default: %(default)s]",
'poisson' : "the Poisson's ratio [default: %(default)s]",
'load' : "the vertical load value (negative means compression)"
" [default: %(default)s]",
'order' : 'displacement field approximation order [default: %(default)s]',
'refine' : 'uniform mesh refinement level [default: %(default)s]',
'probe' : 'probe the results',
}
def main():
from sfepy import data_dir
parser = ArgumentParser(description=__doc__,
formatter_class=RawDescriptionHelpFormatter)
parser.add_argument('--version', action='version', version='%(prog)s')
parser.add_argument('--young', metavar='float', type=float,
action='store', dest='young',
default=2000.0, help=helps['young'])
parser.add_argument('--poisson', metavar='float', type=float,
action='store', dest='poisson',
default=0.4, help=helps['poisson'])
parser.add_argument('--load', metavar='float', type=float,
action='store', dest='load',
default=-1000.0, help=helps['load'])
parser.add_argument('--order', metavar='int', type=int,
action='store', dest='order',
default=1, help=helps['order'])
parser.add_argument('-r', '--refine', metavar='int', type=int,
action='store', dest='refine',
default=0, help=helps['refine'])
parser.add_argument('-p', '--probe',
action="store_true", dest='probe',
default=False, help=helps['probe'])
options = parser.parse_args()
assert_((0.0 < options.poisson < 0.5),
"Poisson's ratio must be in ]0, 0.5[!")
assert_((0 < options.order),
'displacement approximation order must be at least 1!')
output('using values:')
output(" Young's modulus:", options.young)
output(" Poisson's ratio:", options.poisson)
output(' vertical load:', options.load)
output('uniform mesh refinement level:', options.refine)
# Build the problem definition.
mesh = Mesh.from_file(data_dir + '/meshes/2d/its2D.mesh')
domain = FEDomain('domain', mesh)
if options.refine > 0:
for ii in range(options.refine):
output('refine %d...' % ii)
domain = domain.refine()
output('... %d nodes %d elements'
% (domain.shape.n_nod, domain.shape.n_el))
omega = domain.create_region('Omega', 'all')
left = domain.create_region('Left',
'vertices in x < 0.001', 'facet')
bottom = domain.create_region('Bottom',
'vertices in y < 0.001', 'facet')
top = domain.create_region('Top', 'vertex 2', 'vertex')
field = Field.from_args('fu', nm.float64, 'vector', omega,
approx_order=options.order)
u = FieldVariable('u', 'unknown', field)
v = FieldVariable('v', 'test', field, primary_var_name='u')
D = stiffness_from_youngpoisson(2, options.young, options.poisson)
asphalt = Material('Asphalt', D=D)
load = Material('Load', values={'.val' : [0.0, options.load]})
integral = Integral('i', order=2*options.order)
integral0 = Integral('i', order=0)
t1 = Term.new('dw_lin_elastic(Asphalt.D, v, u)',
integral, omega, Asphalt=asphalt, v=v, u=u)
t2 = Term.new('dw_point_load(Load.val, v)',
integral0, top, Load=load, v=v)
eq = Equation('balance', t1 - t2)
eqs = Equations([eq])
xsym = EssentialBC('XSym', bottom, {'u.1' : 0.0})
ysym = EssentialBC('YSym', left, {'u.0' : 0.0})
ls = AutoDirect({})
nls_status = IndexedStruct()
nls = Newton({}, lin_solver=ls, status=nls_status)
pb = Problem('elasticity', equations=eqs)
pb.set_bcs(ebcs=Conditions([xsym, ysym]))
pb.set_solver(nls)
# Solve the problem.
variables = pb.solve()
output(nls_status)
# Postprocess the solution.
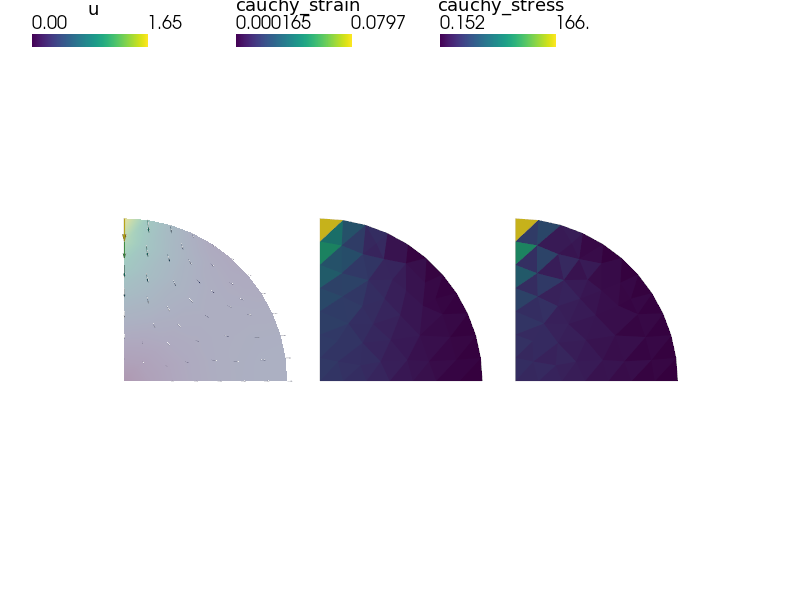
out = variables.create_output()
out = stress_strain(out, pb, variables, extend=True)
pb.save_state('its2D_interactive.vtk', out=out)
gdata = geometry_data['2_3']
nc = len(gdata.coors)
integral_vn = Integral('ivn', coors=gdata.coors,
weights=[gdata.volume / nc] * nc)
nodal_stress(out, pb, variables, integrals=Integrals([integral_vn]))
if options.probe:
# Probe the solution.
probes, labels = gen_lines(pb)
sfield = Field.from_args('sym_tensor', nm.float64, 3, omega,
approx_order=options.order - 1)
stress = FieldVariable('stress', 'parameter', sfield,
primary_var_name='(set-to-None)')
strain = FieldVariable('strain', 'parameter', sfield,
primary_var_name='(set-to-None)')
cfield = Field.from_args('component', nm.float64, 1, omega,
approx_order=options.order - 1)
component = FieldVariable('component', 'parameter', cfield,
primary_var_name='(set-to-None)')
ev = pb.evaluate
order = 2 * (options.order - 1)
strain_qp = ev('ev_cauchy_strain.%d.Omega(u)' % order, mode='qp')
stress_qp = ev('ev_cauchy_stress.%d.Omega(Asphalt.D, u)' % order,
mode='qp', copy_materials=False)
project_by_component(strain, strain_qp, component, order)
project_by_component(stress, stress_qp, component, order)
all_results = []
for ii, probe in enumerate(probes):
fig, results = probe_results(u, strain, stress, probe, labels[ii])
fig.savefig('its2D_interactive_probe_%d.png' % ii)
all_results.append(results)
for ii, results in enumerate(all_results):
output('probe %d:' % ii)
output.level += 2
for key, res in ordered_iteritems(results):
output(key + ':')
val = res[1]
output(' min: %+.2e, mean: %+.2e, max: %+.2e'
% (val.min(), val.mean(), val.max()))
output.level -= 2
if __name__ == '__main__':
main()