linear_elasticity/its2D_1.py¶
Description
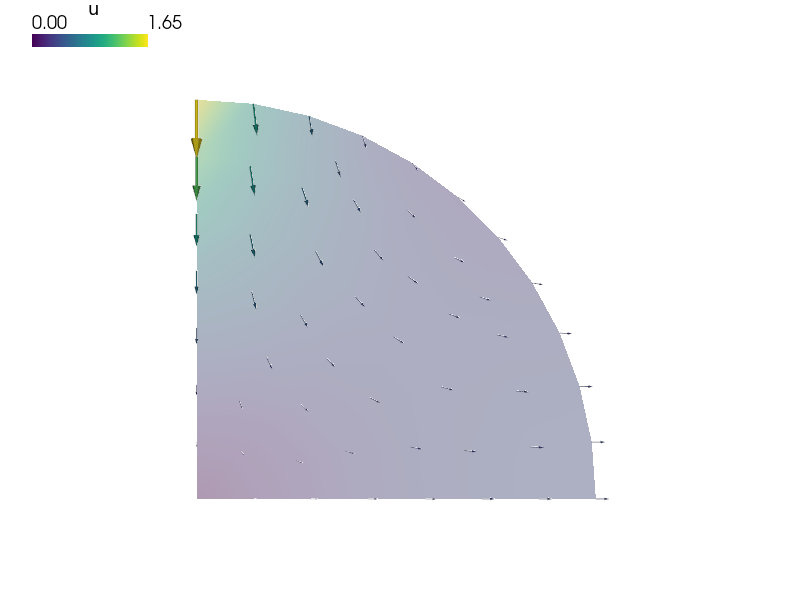
Diametrically point loaded 2-D disk. See Primer.
Find  such that:
such that:
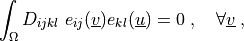
where
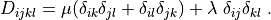
r"""
Diametrically point loaded 2-D disk. See :ref:`sec-primer`.
Find :math:`\ul{u}` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
= 0
\;, \quad \forall \ul{v} \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
"""
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy.discrete.fem.utils import refine_mesh
from sfepy import data_dir
# Fix the mesh file name if you run this file outside the SfePy directory.
filename_mesh = data_dir + '/meshes/2d/its2D.mesh'
refinement_level = 0
filename_mesh = refine_mesh(filename_mesh, refinement_level)
output_dir = '.' # set this to a valid directory you have write access to
young = 2000.0 # Young's modulus [MPa]
poisson = 0.4 # Poisson's ratio
options = {
'output_dir' : output_dir,
}
regions = {
'Omega' : 'all',
'Left' : ('vertices in (x < 0.001)', 'facet'),
'Bottom' : ('vertices in (y < 0.001)', 'facet'),
'Top' : ('vertex 2', 'vertex'),
}
materials = {
'Asphalt' : ({'D': stiffness_from_youngpoisson(2, young, poisson)},),
'Load' : ({'.val' : [0.0, -1000.0]},),
}
fields = {
'displacement': ('real', 'vector', 'Omega', 1),
}
equations = {
'balance_of_forces' :
"""dw_lin_elastic.2.Omega(Asphalt.D, v, u)
= dw_point_load.0.Top(Load.val, v)""",
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
}
ebcs = {
'XSym' : ('Bottom', {'u.1' : 0.0}),
'YSym' : ('Left', {'u.0' : 0.0}),
}
solvers = {
'ls' : ('ls.scipy_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 1,
'eps_a' : 1e-6,
}),
}