large_deformation/hyperelastic_ul_up.py

Description

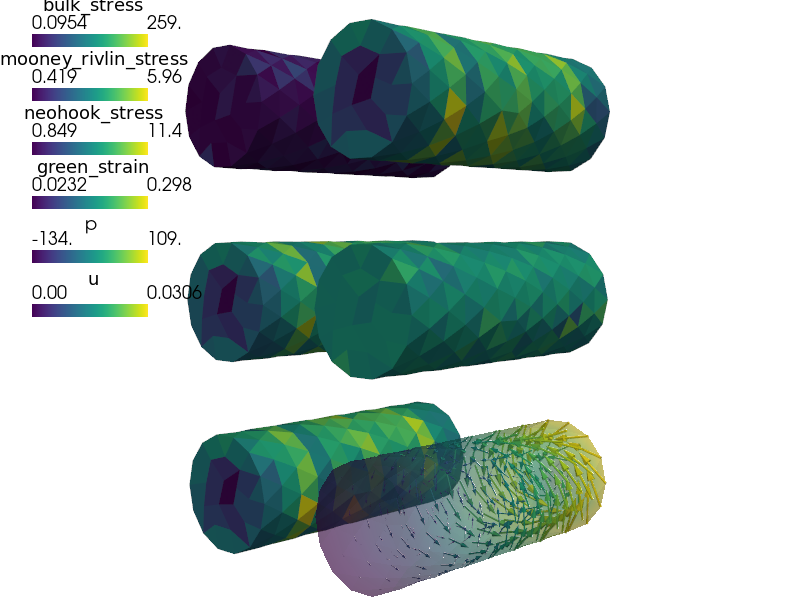
Compressible Mooney-Rivlin hyperelastic material model.

Large deformation is described using the updated Lagrangian formulation. Incompressibility is treated by mixed displacement-pressure formulation. Models of this kind can be used to model e.g. rubber or some biological materials.

source code

# -*- coding: utf-8 -*-
r"""
Compressible Mooney-Rivlin hyperelastic material model.

Large deformation is described using the updated Lagrangian formulation.
Incompressibility is treated by mixed displacement-pressure formulation.
Models of this kind can be used to model e.g. rubber or some biological
materials.
"""
from __future__ import print_function
from __future__ import absolute_import
import numpy as nm
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/3d/cylinder.mesh'

options = {
    'nls': 'newton',
    'ls': 'ls',
    'ts': 'ts',
    'ulf': True,
    'mesh_update_variables': ['u'],
    'output_dir': 'output',
    'post_process_hook': 'stress_strain',
}

fields = {
    'displacement': ('real', 'vector', 'Omega', 1),
    'pressure': ('real', 'scalar', 'Omega', 0),
}

materials = {
    'solid': ({'iK': 1.0 / 1e3, # bulk modulus
               'mu': 20e0, # shear modulus of neoHookean term
               'kappa': 10e0, # shear modulus of Mooney-Rivlin term
               },),
}

variables = {
    'u': ('unknown field', 'displacement', 0),
    'v': ('test field', 'displacement', 'u'),
    'p': ('unknown field', 'pressure', 1),
    'q': ('test field', 'pressure', 'p'),
}

regions = {
    'Omega' : 'all',
    'Left' : ('vertices in (x < 0.001)', 'facet'),
    'Right' : ('vertices in (x > 0.099)', 'facet'),
}

##
# Dirichlet BC + related functions.
ebcs = {
    'l' : ('Left', {'u.all' : 0.0}),
    'r' : ('Right', {'u.0' : 0.0, 'u.[1,2]' : 'rotate_yz'}),
}

centre = nm.array( [0, 0], dtype = nm.float64 )

def rotate_yz(ts, coor, **kwargs):
    from sfepy.linalg import rotation_matrix2d

    vec = coor[:,1:3] - centre

    angle = 10.0 * ts.step
    print('angle:', angle)

    mtx = rotation_matrix2d( angle )
    vec_rotated = nm.dot( vec, mtx )

    displacement = vec_rotated - vec

    return displacement

functions = {
    'rotate_yz' : (rotate_yz,),
}

def stress_strain( out, problem, state, extend = False ):
    from sfepy.base.base import Struct

    ev = problem.evaluate
    strain = ev('dw_ul_he_neohook.3.Omega( solid.mu, v, u )',
                mode='el_avg', term_mode='strain')
    out['green_strain'] = Struct(name='output_data',
                                 mode='cell', data=strain, dofs=None)

    stress = ev('dw_ul_he_neohook.3.Omega( solid.mu, v, u )',
                mode='el_avg', term_mode='stress')
    out['neohook_stress'] = Struct(name='output_data',
                                   mode='cell', data=stress, dofs=None)

    stress = ev('dw_ul_he_mooney_rivlin.3.Omega( solid.kappa, v, u )',
                mode='el_avg', term_mode='stress')
    out['mooney_rivlin_stress'] = Struct(name='output_data',
                                         mode='cell', data=stress, dofs=None)

    stress = ev('dw_ul_bulk_pressure.3.Omega( v, u, p )',
                mode='el_avg', term_mode= 'stress')
    out['bulk_stress'] = Struct(name='output_data',
                                mode='cell', data=stress, dofs=None)

    return out

equations = {
    'balance': """dw_ul_he_neohook.3.Omega( solid.mu, v, u )
                + dw_ul_he_mooney_rivlin.3.Omega(solid.kappa, v, u)
                + dw_ul_bulk_pressure.3.Omega( v, u, p ) = 0""",
    'volume': """dw_ul_volume.3.Omega( q, u )
               + dw_ul_compressible.3.Omega( solid.iK, q, p, u ) = 0"""
    }

##
# Solvers etc.
solvers = {
    'ls': ('ls.scipy_direct', {}),
    'newton': ('nls.newton', {
        'i_max': 25,
        'eps_a': 1e-8,
        'eps_r': 1.0,
        'macheps': 1e-16,
        'lin_red': 1e-2, # Linear system error < (eps_a * lin_red).
        'ls_red': 0.1,
        'ls_red_warp': 0.001,
        'ls_on': 1.1,
        'ls_min': 1e-5,
        'check': 0,
        'delta': 1e-6,
        }),
    'ts': ('ts.simple', {
        't0': 0,
        't1': 1,
        'dt': None,
        'n_step': 11, # has precedence over dt!
        'verbose' : 1,
        }),
    }