large_deformation/hyperelastic_ul.py

Description

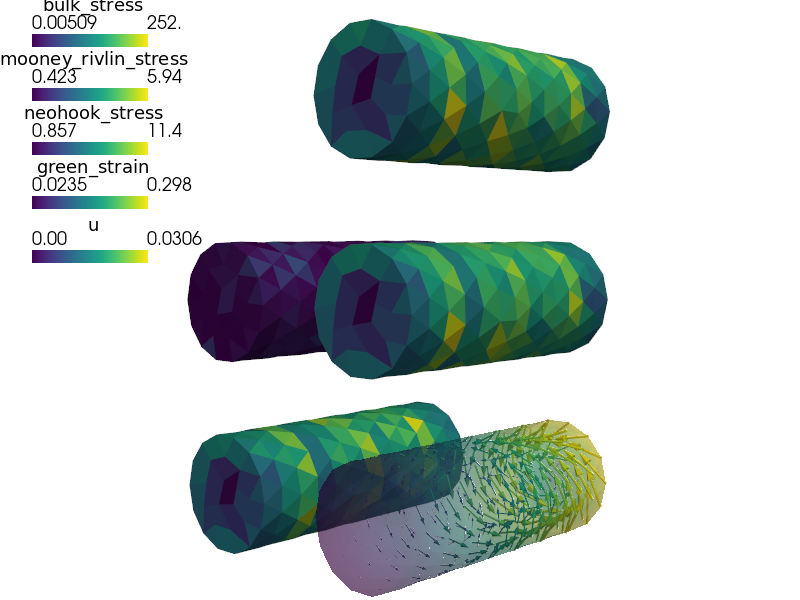
Nearly incompressible Mooney-Rivlin hyperelastic material model.

Large deformation is described using the updated Lagrangian formulation. Models of this kind can be used to model e.g. rubber or some biological materials.

source code

# -*- coding: utf-8 -*-
r"""
Nearly incompressible Mooney-Rivlin hyperelastic material model.

Large deformation is described using the updated Lagrangian formulation.
Models of this kind can be used to model e.g. rubber or some biological
materials.
"""
import numpy as nm
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/3d/cylinder.mesh'

options = {
    'nls': 'newton',
    'ls': 'ls',
    'ts': 'ts',
    'ulf': True,
    'mesh_update_variables': ['u'],
    'output_dir': 'output',
    'post_process_hook': 'stress_strain',
    'report_nls_status': True,
    'log_nls_status': True,
}

fields = {
    'displacement': ('real', 3, 'Omega', 1),
}

materials = {
    'solid': ({'K': 1e3, # bulk modulus
               'mu': 20e0, # shear modulus of neoHookean term
               'kappa': 10e0, # shear modulus of Mooney-Rivlin term
               },),
}

variables = {
    'u': ('unknown field', 'displacement', 0),
    'v': ('test field', 'displacement', 'u'),
}

regions = {
    'Omega' : 'all',
    'Left' : ('vertices in (x < 0.001)', 'facet'),
    'Right' : ('vertices in (x > 0.099)', 'facet'),
}

##
# Dirichlet BC + related functions.
ebcs = {
    'l' : ('Left', {'u.all' : 0.0}),
    'r' : ('Right', {'u.0' : 0.0, 'u.[1,2]' : 'rotate_yz'}),
}

centre = nm.array( [0, 0], dtype = nm.float64 )

def rotate_yz(ts, coor, **kwargs):
    from sfepy.linalg import rotation_matrix2d

    vec = coor[:,1:3] - centre

    angle = 10.0 * ts.step
    print('angle:', angle)

    mtx = rotation_matrix2d( angle )
    vec_rotated = nm.dot( vec, mtx )

    displacement = vec_rotated - vec

    return displacement

functions = {
    'rotate_yz' : (rotate_yz,),
}

def stress_strain( out, problem, state, extend = False ):
    from sfepy.base.base import Struct

    ev = problem.evaluate
    strain = ev('dw_ul_he_neohook.3.Omega( solid.mu, v, u )',
                mode='el_avg', term_mode='strain')
    out['green_strain'] = Struct(name='output_data',
                                 mode='cell', data=strain, dofs=None)

    stress = ev('dw_ul_he_neohook.3.Omega( solid.mu, v, u )',
                mode='el_avg', term_mode='stress')
    out['neohook_stress'] = Struct(name='output_data',
                                   mode='cell', data=stress, dofs=None)

    stress = ev('dw_ul_he_mooney_rivlin.3.Omega( solid.kappa, v, u )',
                mode='el_avg', term_mode='stress')
    out['mooney_rivlin_stress'] = Struct(name='output_data',
                                         mode='cell', data=stress, dofs=None)

    stress = ev('dw_ul_bulk_penalty.3.Omega( solid.K, v, u )',
                mode='el_avg', term_mode= 'stress')
    out['bulk_stress'] = Struct(name='output_data',
                                mode='cell', data=stress, dofs=None)

    return out

equations = {
    'balance': """dw_ul_he_neohook.3.Omega( solid.mu, v, u )
                + dw_ul_he_mooney_rivlin.3.Omega(solid.kappa, v, u)
                + dw_ul_bulk_penalty.3.Omega( solid.K, v, u )
                = 0""",
    }

##
# Solvers etc.
solvers = {
    'ls': ('ls.scipy_direct', {}),
    'newton': ('nls.newton', {
        'i_max': 25,
        'eps_a': 1e-8,
        'eps_r': 1.0,
        'macheps': 1e-16,
        'lin_red': 1e-2, # Linear system error < (eps_a * lin_red).
        'ls_red': 0.1,
        'ls_red_warp': 0.001,
        'ls_on': 1.1,
        'ls_min': 1e-5,
        'check': 0,
        'delta': 1e-6,
        }),
    'ts': ('ts.simple', {
        't0': 0,
        't1': 1,
        'dt': None,
        'n_step': 11, # has precedence over dt!
        'verbose' : 1,
        }),
    }