large_deformation/gen_yeoh_tl_up_interactive.py¶

Description

Incompressible generalized Yeoh hyperelastic material model.

In this model, the deformation energy density per unit reference volume is given by

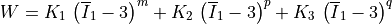
$W = K_1 \, \left( \overline I_1 - 3 \right)^{m} +K_2 \, \left( \overline I_1 - 3 \right)^{p} +K_3 \, \left( \overline I_1 - 3 \right)^{q}$

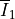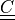where $\overline I_1$ is the first main invariant of the deviatoric part of the right Cauchy-Green deformation tensor $\ull{C}$ , the coefficients 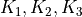$K_1, K_2, K_3$ and exponents 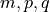$m, p, q$ are material parameters. Only a single term (dw_tl_he_genyeoh) is used in this example for the sake of simplicity.

Components of the second Piola-Kirchhoff stress are in the case of an incompressible material

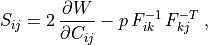
$S_{ij} = 2 \, \pdiff{W}{C_{ij}} - p \, F^{-1}_{ik} \, F^{-T}_{kj} \;,$

where $p$ is the hydrostatic pressure.

The large deformation is described using the total Lagrangian formulation in this example. The incompressibility is treated by mixed displacement-pressure formulation. The weak formulation is: Find the displacement field $\ul{u}$ and pressure field $p$ such that:

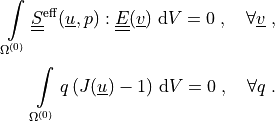
$\intl{\Omega\suz}{} \ull{S}\eff(\ul{u}, p) : \ull{E}(\ul{v}) \difd{V} = 0 \;, \quad \forall \ul{v} \;, \intl{\Omega\suz}{} q\, (J(\ul{u})-1) \difd{V} = 0 \;, \quad \forall q \;.$

The following formula holds for the axial true (Cauchy) stress in the case of uniaxial stress:

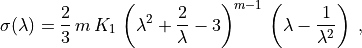
$\sigma(\lambda) = \frac{2}{3} \, m \, K_1 \, \left( \lambda^2 + \frac{2}{\lambda} - 3 \right)^{m-1} \, \left( \lambda - \frac{1}{\lambda^2} \right) \;,$

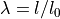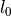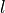where $\lambda = l/l_0$ is the prescribed stretch ( $l_0$ and $l$ being the original and deformed specimen length respectively).

The boundary conditions are set so that a state of uniaxial stress is achieved, i.e. appropriate components of displacement are fixed on the “Left”, “Bottom”, and “Near” faces and a monotonously increasing displacement is prescribed on the “Right” face. This prescribed displacement is then used to calculate 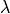$\lambda$ and to convert the second Piola-Kirchhoff stress to the true (Cauchy) stress.

Note on material parameters¶

The three-term generalized Yeoh model is meant to be used for modelling of filled rubbers. The following choice of parameters is suggested [1] based on experimental data and stability considerations:

$K_1 > 0$ ,

$K_2 < 0$ ,

$K_3 > 0$ ,

$0.7 < m < 1$ ,

$m < p < q$ .

Usage Examples¶

Default options:

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py

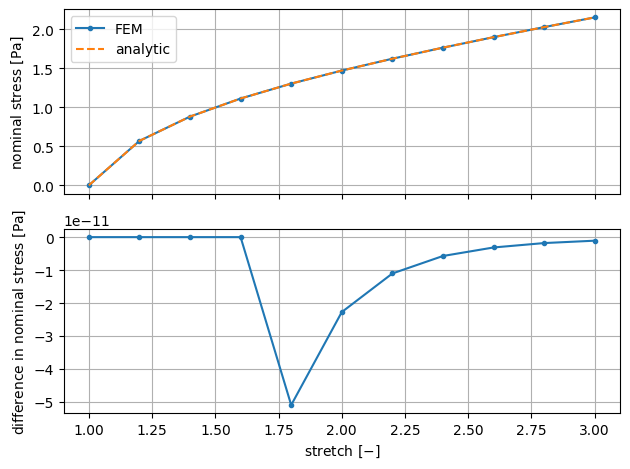
To show a comparison of stress against the analytic formula:

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py -p

Using different mesh fineness:

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
  --shape "5, 5, 5"

Different dimensions of the computational domain:

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
  --dims "2, 1, 3"

Different length of time interval and/or number of time steps:

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
  -t 0,15,21

Use higher approximation order (the -t option to decrease the time step is required for convergence here):

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
  --order 2 -t 0,2,21

Change material parameters:

python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py -m 2,1

View the results using `sfepy-view`¶

Show pressure on deformed mesh (use PgDn/PgUp to jump forward/back):

sfepy-view --fields=p:f1:wu:p1 domain.??.vtk

Show the axial component of stress (second Piola-Kirchhoff):

sfepy-view --fields=stress:c0 domain.??.vtk

[1] Travis W. Hohenberger, Richard J. Windslow, Nicola M. Pugno, James J. C. Busfield. Aconstitutive Model For Both Lowand High Strain Nonlinearities In Highly Filled Elastomers And Implementation With User-Defined Material Subroutines In Abaqus. Rubber Chemistry And Technology, Vol. 92, No. 4, Pp. 653-686 (2019)

../_images/large_deformation-gen_yeoh_tl_up_interactive-gen_yeoh_tl_up_comparison1.png

../_images/large_deformation-gen_yeoh_tl_up_interactive.png

source code

#!/usr/bin/env python
r"""
Incompressible generalized Yeoh hyperelastic material model.

In this model, the deformation energy density per unit reference volume is
given by

.. math::
    W =
      K_1 \, \left( \overline I_1 - 3 \right)^{m}
      +K_2 \, \left( \overline I_1 - 3 \right)^{p}
      +K_3 \, \left( \overline I_1 - 3 \right)^{q}

where :math:`\overline I_1` is the first main invariant of the deviatoric part
of the right Cauchy-Green deformation tensor :math:`\ull{C}`, the coefficients
:math:`K_1, K_2, K_3` and exponents :math:`m, p, q` are material parameters.
Only a single term (:class:`dw_tl_he_genyeoh
<sfepy.terms.terms_hyperelastic_tl.GenYeohTLTerm>`) is used in this example for
the sake of simplicity.

Components of the second Piola-Kirchhoff stress are in the case of an
incompressible material

.. math::
    S_{ij} = 2 \, \pdiff{W}{C_{ij}} - p \, F^{-1}_{ik} \, F^{-T}_{kj} \;,

where :math:`p` is the hydrostatic pressure.

The large deformation is described using the total Lagrangian formulation in
this example. The incompressibility is treated by mixed displacement-pressure
formulation. The weak formulation is:
Find the displacement field :math:`\ul{u}` and pressure field :math:`p`
such that:

.. math::
    \intl{\Omega\suz}{} \ull{S}\eff(\ul{u}, p) : \ull{E}(\ul{v})
    \difd{V} = 0
    \;, \quad \forall \ul{v} \;,

    \intl{\Omega\suz}{} q\, (J(\ul{u})-1) \difd{V} = 0
    \;, \quad \forall q \;.

The following formula holds for the axial true (Cauchy) stress in the case of
uniaxial stress:

.. math::
    \sigma(\lambda) =
        \frac{2}{3} \, m \, K_1 \,
        \left( \lambda^2 + \frac{2}{\lambda} - 3 \right)^{m-1} \,
        \left( \lambda - \frac{1}{\lambda^2} \right) \;,

where :math:`\lambda = l/l_0` is the prescribed stretch (:math:`l_0` and
:math:`l` being the original and deformed specimen length respectively).

The boundary conditions are set so that a state of uniaxial stress is achieved,
i.e. appropriate components of displacement are fixed on the "Left", "Bottom",
and "Near" faces and a monotonously increasing displacement is prescribed on
the "Right" face. This prescribed displacement is then used to calculate
:math:`\lambda` and to convert the second Piola-Kirchhoff stress to the true
(Cauchy) stress.

Note on material parameters
---------------------------

The three-term generalized Yeoh model is meant to be used for modelling of
filled rubbers. The following choice of parameters is suggested [1] based on
experimental data and stability considerations:

  :math:`K_1 > 0`,

  :math:`K_2 < 0`,

  :math:`K_3 > 0`,

  :math:`0.7 < m < 1`,

  :math:`m < p < q`.

Usage Examples
--------------

Default options::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py

To show a comparison of stress against the analytic formula::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py -p

Using different mesh fineness::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
    --shape "5, 5, 5"

Different dimensions of the computational domain::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
    --dims "2, 1, 3"

Different length of time interval and/or number of time steps::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
    -t 0,15,21

Use higher approximation order (the ``-t`` option to decrease the time step is
required for convergence here)::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py \
    --order 2 -t 0,2,21

Change material parameters::

  python3 sfepy/examples/large_deformation/gen_yeoh_tl_up_interactive.py -m 2,1

View the results using ``sfepy-view``
-------------------------------------

Show pressure on deformed mesh (use PgDn/PgUp to jump forward/back)::

  sfepy-view --fields=p:f1:wu:p1 domain.??.vtk

Show the axial component of stress (second Piola-Kirchhoff)::

  sfepy-view --fields=stress:c0 domain.??.vtk

[1] Travis W. Hohenberger, Richard J. Windslow, Nicola M. Pugno, James J. C.
Busfield. Aconstitutive Model For Both Lowand High Strain Nonlinearities In
Highly Filled Elastomers And Implementation With User-Defined Material
Subroutines In Abaqus. Rubber Chemistry And Technology, Vol. 92, No. 4, Pp.
653-686 (2019)
"""
from __future__ import print_function, absolute_import
import argparse
import sys

SFEPY_DIR = '.'
sys.path.append(SFEPY_DIR)

import matplotlib.pyplot as plt
import numpy as np

from sfepy.base.base import IndexedStruct, Struct
from sfepy.discrete import (
    FieldVariable, Material, Integral, Function, Equation, Equations, Problem)
from sfepy.discrete.conditions import Conditions, EssentialBC
from sfepy.discrete.fem import FEDomain, Field
from sfepy.homogenization.utils import define_box_regions
from sfepy.mesh.mesh_generators import gen_block_mesh
from sfepy.solvers.ls import ScipyDirect
from sfepy.solvers.nls import Newton
from sfepy.solvers.ts_solvers import SimpleTimeSteppingSolver
from sfepy.terms import Term

DIMENSION = 3

def get_displacement(ts, coors, bc=None, problem=None):
    """
    Define the time-dependent displacement.
    """
    out = 1. * ts.time * coors[:, 0]
    return out

def _get_analytic_stress(stretches, coef, exp):
    out =  np.array([
        2 * coef * exp * (stretch**2 + 2 / stretch - 3)**(exp - 1)
        * (stretch - stretch**-2)
        if (stretch**2 + 2 / stretch > 3) else 0.
        for stretch in stretches])
    return out

def plot_graphs(
        material_parameters, global_stress, global_displacement,
        undeformed_length):
    """
    Plot a comparison of the nominal stress computed by the FEM and using the
    analytic formula.

    Parameters
    ----------
    material_parameters : list or tuple of float
        The K_1 coefficient and exponent m.
    global_displacement
        The total displacement for each time step, from the FEM.
    global_stress
        The true (Cauchy) stress for each time step, from the FEM.
    undeformed_length : float
        The length of the undeformed specimen.
    """
    coef, exp = material_parameters

    stretch = 1 + np.array(global_displacement) / undeformed_length

    # axial stress values
    stress_fem_2pk = np.array([sig for sig in global_stress])
    stress_fem = stress_fem_2pk * stretch
    stress_analytic = _get_analytic_stress(stretch, coef, exp)

    fig, (ax_stress, ax_difference) = plt.subplots(nrows=2, sharex=True)

    ax_stress.plot(stretch, stress_fem, '.-', label='FEM')
    ax_stress.plot(stretch, stress_analytic, '--', label='analytic')

    ax_difference.plot(stretch, stress_fem - stress_analytic, '.-')

    ax_stress.legend(loc='best').set_draggable(True)
    ax_stress.set_ylabel(r'nominal stress $\mathrm{[Pa]}$')
    ax_stress.grid()

    ax_difference.set_ylabel(r'difference in nominal stress $\mathrm{[Pa]}$')
    ax_difference.set_xlabel(r'stretch $\mathrm{[-]}$')
    ax_difference.grid()
    plt.tight_layout()

    return fig

def stress_strain(
        out, problem, _state, order=1, global_stress=None,
        global_displacement=None, **_):
    """
    Compute the stress and the strain and add them to the output.

    Parameters
    ----------
    out : dict
        Holds the results of the finite element computation.
    problem : sfepy.discrete.Problem
    order : int
        The approximation order of the displacement field.
    global_displacement
        Total displacement for each time step, current value will be appended.
    global_stress
        The true (Cauchy) stress for each time step, current value will be
        appended.

    Returns
    -------
    out : dict
    """
    strain = problem.evaluate(
        'dw_tl_he_genyeoh.%d.Omega(m1.par, v, u)' % (2*order),
        mode='el_avg', term_mode='strain', copy_materials=False)

    out['green_strain'] = Struct(
        name='output_data', mode='cell', data=strain, dofs=None)

    stress_1 = problem.evaluate(
        'dw_tl_he_genyeoh.%d.Omega(m1.par, v, u)' % (2*order),
        mode='el_avg', term_mode='stress', copy_materials=False)
    stress_p = problem.evaluate(
        'dw_tl_bulk_pressure.%d.Omega(v, u, p)' % (2*order),
        mode='el_avg', term_mode='stress', copy_materials=False)
    stress = stress_1 + stress_p

    out['stress'] = Struct(
        name='output_data', mode='cell', data=stress, dofs=None)

    global_stress.append(stress[0, 0, 0, 0])
    global_displacement.append(get_displacement(
        problem.ts, np.array([[1., 0, 0]]))[0])

    return out

def main(cli_args):
    dims = parse_argument_list(cli_args.dims, float)
    shape = parse_argument_list(cli_args.shape, int)
    centre = parse_argument_list(cli_args.centre, float)
    material_parameters = parse_argument_list(cli_args.material_parameters,
                                              float)
    order = cli_args.order

    ts_vals = cli_args.ts.split(',')
    ts = {
        't0' : float(ts_vals[0]), 't1' : float(ts_vals[1]),
        'n_step' : int(ts_vals[2])}

    do_plot = cli_args.plot

    ### Mesh and regions ###
    mesh = gen_block_mesh(
        dims, shape, centre, name='block', verbose=False)
    domain = FEDomain('domain', mesh)

    omega = domain.create_region('Omega', 'all')

    lbn, rtf = domain.get_mesh_bounding_box()
    box_regions = define_box_regions(3, lbn, rtf)
    regions = dict([
        [r, domain.create_region(r, box_regions[r][0], box_regions[r][1])]
        for r in box_regions])

    ### Fields ###
    scalar_field = Field.from_args(
        'fu', np.float64, 'scalar', omega, approx_order=order-1)
    vector_field = Field.from_args(
        'fv', np.float64, 'vector', omega, approx_order=order)

    u = FieldVariable('u', 'unknown', vector_field, history=1)
    v = FieldVariable('v', 'test', vector_field, primary_var_name='u')
    p = FieldVariable('p', 'unknown', scalar_field, history=1)
    q = FieldVariable('q', 'test', scalar_field, primary_var_name='p')

    ### Material ###
    coefficient, exponent  = material_parameters
    m_1 = Material(
        'm1', par=[coefficient, exponent],
    )

    ### Boundary conditions ###
    x_sym = EssentialBC('x_sym', regions['Left'], {'u.0' : 0.0})
    y_sym = EssentialBC('y_sym', regions['Near'], {'u.1' : 0.0})
    z_sym = EssentialBC('z_sym', regions['Bottom'], {'u.2' : 0.0})
    disp_fun = Function('disp_fun', get_displacement)
    displacement = EssentialBC(
        'displacement', regions['Right'], {'u.0' : disp_fun})
    ebcs = Conditions([x_sym, y_sym, z_sym, displacement])

    ### Terms and equations ###
    integral = Integral('i', order=2*order+1)

    term_1 = Term.new(
        'dw_tl_he_genyeoh(m1.par, v, u)',
        integral, omega, m1=m_1, v=v, u=u)
    term_pressure = Term.new(
        'dw_tl_bulk_pressure(v, u, p)',
        integral, omega, v=v, u=u, p=p)

    term_volume_change = Term.new(
        'dw_tl_volume(q, u)',
        integral, omega, q=q, u=u, term_mode='volume')
    term_volume = Term.new(
        'dw_integrate(q)',
        integral, omega, q=q)

    eq_balance = Equation('balance', term_1 + term_pressure)
    eq_volume = Equation('volume', term_volume_change - term_volume)
    equations = Equations([eq_balance, eq_volume])

    ### Solvers ###
    ls = ScipyDirect({})
    nls_status = IndexedStruct()
    nls = Newton(
        {'i_max' : 20},
        lin_solver=ls, status=nls_status
    )

    ### Problem ###
    pb = Problem('hyper', equations=equations)
    pb.set_bcs(ebcs=ebcs)
    pb.set_ics(ics=Conditions([]))
    tss = SimpleTimeSteppingSolver(ts, nls=nls, context=pb)
    pb.set_solver(tss)

    ### Solution ###
    axial_stress = []
    axial_displacement = []
    def stress_strain_fun(*args, **kwargs):
        return stress_strain(
            *args, order=order, global_stress=axial_stress,
            global_displacement=axial_displacement, **kwargs)

    pb.solve(save_results=True, post_process_hook=stress_strain_fun)

    if do_plot:
        fig = plot_graphs(
            material_parameters, axial_stress, axial_displacement,
            undeformed_length=dims[0])

        fig.savefig('gen_yeoh_tl_up_comparison.png', bbox_inches='tight')

        if cli_args.show:
            plt.show()

def parse_argument_list(cli_arg, type_fun=None, value_separator=','):
    """
    Split the command-line argument into a list of items of given type.

    Parameters
    ----------
    cli_arg : str
    type_fun : function
        A function to be called on each substring of `cli_arg`; default: str.
    value_separator : str
    """
    if type_fun is None:
        type_fun = str
    out = [type_fun(value) for value in cli_arg.split(value_separator)]
    return out

def parse_args():
    """Parse command line arguments."""
    parser = argparse.ArgumentParser(
        description=__doc__,
        formatter_class=argparse.RawDescriptionHelpFormatter)
    parser.add_argument(
        '--order', type=int, default=1, help='The approximation order of the '
        'displacement field [default: %(default)s]')
    parser.add_argument(
        '-m', '--material-parameters', default='0.5, 0.9',
        help='Material parameters - coefficient and exponent - of a single '
        'term of the generalized Yeoh hyperelastic model. '
        '[default: %(default)s]')
    parser.add_argument(
        '--dims', default="1.0, 1.0, 1.0",
        help='Dimensions of the block [default: %(default)s]')
    parser.add_argument(
        '--shape', default='2, 2, 2',
        help='Shape (counts of nodes in x, y, z) of the block [default: '
        '%(default)s]')
    parser.add_argument(
        '--centre', default='0.5, 0.5, 0.5',
        help='Centre of the block [default: %(default)s]')
    parser.add_argument(
        '-p', '--plot', action='store_true', default=False,
        help='Whether to plot a comparison with analytical formula.')
    parser.add_argument(
        '-n', '--no-show', dest='show', action='store_false', default=True,
        help='Do not show matplotlib figures.')
    parser.add_argument(
        '-t', '--ts',
        type=str, default='0.0,2.0,11',
        help='Start time, end time, and number of time steps [default: '
        '"%(default)s"]')
    return parser.parse_args()

if __name__ == '__main__':
    args = parse_args()
    main(args)

large_deformation/gen_yeoh_tl_up_interactive.py¶

Note on material parameters¶

Usage Examples¶

View the results using sfepy-view¶

View the results using `sfepy-view`¶