diffusion/darcy_flow_multicomp.py¶
Description
Each of the two equations describes a flow in one compartment of a porous
medium. The equations are based on the Darcy flow and the i-th compartment is
defined in 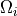 .
.
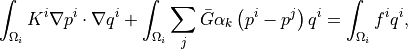
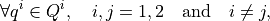
where 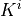 is the local permeability of the i-th compartment,
is the local permeability of the i-th compartment,
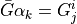 is the perfusion coefficient
related to the compartments
is the perfusion coefficient
related to the compartments 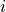 and
and 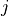 ,
, 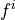 are
sources or sinks which represent the external flow into the i-th
compartment and
are
sources or sinks which represent the external flow into the i-th
compartment and 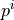 is the pressure in the i-th compartment.
is the pressure in the i-th compartment.
r"""
Each of the two equations describes a flow in one compartment of a porous
medium. The equations are based on the Darcy flow and the i-th compartment is
defined in :math:`\Omega_{i}`.
.. math::
\int_{\Omega_{i}} K^{i} \nabla p^{i} \cdot \nabla q^{i}+\int_{\Omega_{i}}
\sum_{j} \bar{G}\alpha_{k} \left( p^{i}-p^{j} \right)q^{i}
= \int_{\Omega_{i}} f^{i} q^{i},
.. math::
\forall q^{i} \in Q^{i}, \quad i,j=1,2 \quad \mbox{and} \quad i\neq j,
where :math:`K^{i}` is the local permeability of the i-th compartment,
:math:`\bar{G}\alpha_{k} = G^{i}_{j}` is the perfusion coefficient
related to the compartments :math:`i` and :math:`j`, :math:`f^i` are
sources or sinks which represent the external flow into the i-th
compartment and :math:`p^{i}` is the pressure in the i-th compartment.
"""
from sfepy.base.base import Struct
import numpy as nm
from sfepy import data_dir
filename_mesh = data_dir + '/meshes/3d/cube_medium_hexa.mesh'
G_bar = 2.0
alpha1 = 1.3
alpha2 = 1.0
materials = {
'mat': ('mat_fun')
}
regions = {
'Omega': 'cells of group 0',
'Sigma_1': ('vertex 0', 'vertex'),
'Omega1': ('copy r.Omega', 'cell', 'Omega'),
'Omega2': ('copy r.Omega', 'cell', 'Omega'),
'Source': 'cell 24',
'Sink': 'cell 1',
}
fields = {
'pressure':('real', 1, 'Omega', 1)
}
variables = {
'p1': ('unknown field', 'pressure'),
'q1': ('test field', 'pressure', 'p1'),
'p2': ('unknown field', 'pressure'),
'q2': ('test field', 'pressure', 'p2'),
}
ebcs = {
'P1': ('Sigma_1', {'p1.0' : 0.0}),
}
equations = {
'komp1': """dw_diffusion.5.Omega1(mat.K, q1, p1)
+ dw_dot.5.Omega1(mat.G_alfa, q1, p1)
- dw_dot.5.Omega1(mat.G_alfa, q1, p2)
= dw_integrate.5.Source(mat.f_1, q1)""",
'komp2': """dw_diffusion.5.Omega2(mat.K, q2, p2)
+ dw_dot.5.Omega2(mat.G_alfa, q2, p2)
- dw_dot.5.Omega2(mat.G_alfa, q2, p1)
= dw_integrate.5.Sink(mat.f_2, q2)"""
}
solvers = {
'ls': ('ls.scipy_direct', {}),
'newton': ('nls.newton',
{'i_max' : 1,
'eps_a' : 1e-6,
'eps_r' : 1.0,
})
}
def mat_fun(ts, coors, mode=None, **kwargs):
if mode == 'qp':
nqp, dim = coors.shape
alpha = nm.zeros((nqp,1,1), dtype=nm.float64)
alpha[0:nqp // 2,...] = alpha1
alpha[nqp // 2:,...] = alpha2
K = nm.eye(dim, dtype=nm.float64)
K2 = nm.tile(K, (nqp,1,1))
out = {
'K' : K2,
'f_1': 20.0 * nm.ones((nqp,1,1), dtype=nm.float64),
'f_2': -20.0 * nm.ones((nqp,1,1), dtype=nm.float64),
'G_alfa': G_bar * alpha,
}
return out
functions = {
'mat_fun': (mat_fun,),
}
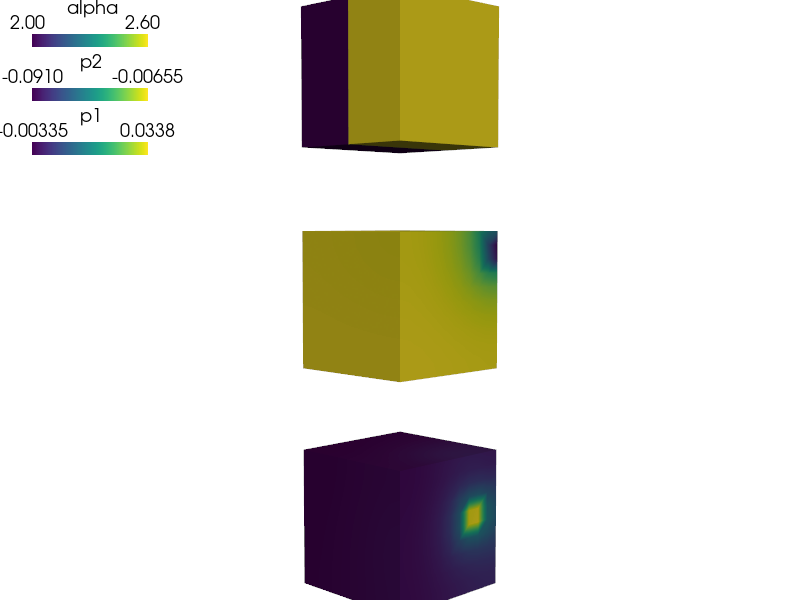
options = {
'post_process_hook': 'postproc',
}
def postproc(out, pb, state, extend=False):
alpha = pb.evaluate('ev_integrate_mat.5.Omega(mat.G_alfa, p1)',
mode='el_avg')
out['alpha'] = Struct(name='output_data',
mode='cell',
data=alpha.reshape(alpha.shape[0], 1, 1, 1),
dofs=None)
return out