diffusion/cube.py

Description

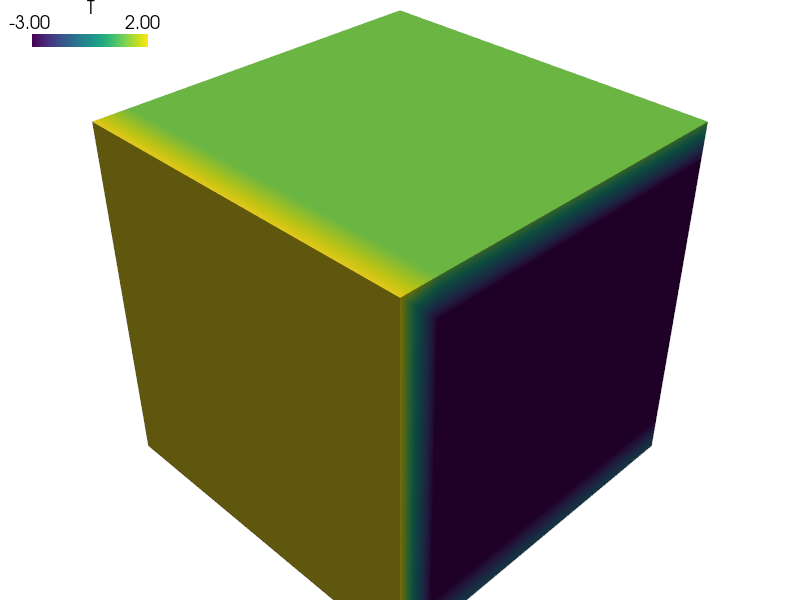
Laplace equation (e.g. temperature distribution) on a cube geometry with different boundary condition values on the cube sides. This example was used to create the SfePy logo.

Find 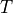such that:

source code

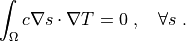
r"""
Laplace equation (e.g. temperature distribution) on a cube geometry with
different boundary condition values on the cube sides. This example was
used to create the SfePy logo.

Find :math:`T` such that:

.. math::
    \int_{\Omega} c \nabla s \cdot \nabla T
    = 0
    \;, \quad \forall s \;.
"""
from __future__ import absolute_import
from sfepy import data_dir

#filename_mesh = data_dir + '/meshes/3d/cube_big_tetra.mesh'
filename_mesh = data_dir + '/meshes/3d/cube_medium_hexa.mesh'

############# Laplace.

material_1 = {
    'name' : 'coef',
    'values' : {'val' : 1.0},
}

field_1 = {
    'name' : 'temperature',
    'dtype' : 'real',
    'shape' : (1,),
    'region' : 'Omega',
    'approx_order' : 1,
}

if filename_mesh.find('cube_medium_hexa.mesh') >= 0:
    region_1000 = {
        'name' : 'Omega',
        'select' : 'cells of group 0',
    }
    integral_1 = {
        'name' : 'i',
        'order' : 1,
    }
    solver_0 = {
        'name' : 'ls',
        'kind' : 'ls.scipy_direct',
    }

elif filename_mesh.find('cube_big_tetra.mesh') >= 0:
    region_1000 = {
        'name' : 'Omega',
        'select' : 'cells of group 6',
    }
    integral_1 = {
        'name' : 'i',
        'quadrature' : 'custom',
        'vals'    : [[1./3., 1./3., 1./3.]],
        'weights' : [0.5]
    }
    solver_0 = {
        'name' : 'ls',
        'kind' : 'ls.scipy_iterative',

        'method' : 'cg',
        'i_max'   : 1000,
        'eps_r'   : 1e-12,
    }

variable_1 = {
    'name' : 'T',
    'kind' : 'unknown field',
    'field' : 'temperature',
    'order' : 0, # order in the global vector of unknowns
}

variable_2 = {
    'name' : 's',
    'kind' : 'test field',
    'field' : 'temperature',
    'dual' : 'T',
}

region_0 = {
    'name' : 'Surface',
    'select' : 'vertices of surface',
    'kind' : 'facet',
}
region_1 = {
    'name' : 'Bottom',
    'select' : 'vertices in (z < -0.4999999)',
    'kind' : 'facet',
}
region_2 = {
    'name' : 'Top',
    'select' : 'vertices in (z > 0.4999999)',
    'kind' : 'facet',
}
region_03 = {
    'name' : 'Left',
    'select' : 'vertices in (x < -0.4999999)',
    'kind' : 'facet',
}

ebc_1 = {
    'name' : 'T0',
    'region' : 'Surface',
    'dofs' : {'T.0' : -3.0},
}
ebc_4 = {
    'name' : 'T1',
    'region' : 'Top',
    'dofs' : {'T.0' : 1.0},
}
ebc_3 = {
    'name' : 'T2',
    'region' : 'Bottom',
    'dofs' : {'T.0' : -1.0},
}
ebc_2 = {
    'name' : 'T3',
    'region' : 'Left',
    'dofs' : {'T.0' : 2.0},
}

equations = {
    'nice_equation' : """dw_laplace.i.Omega( coef.val, s, T ) = 0""",
}

solver_1 = {
    'name' : 'newton',
    'kind' : 'nls.newton',

    'i_max'      : 1,
    'eps_a'      : 1e-10,
    'eps_r'      : 1.0,
    'macheps'   : 1e-16,
    'lin_red'    : 1e-2, # Linear system error < (eps_a * lin_red).
    'ls_red'     : 0.1,
    'ls_red_warp' : 0.001,
    'ls_on'      : 1.1,
    'ls_min'     : 1e-5,
    'check'     : 0,
    'delta'     : 1e-6,
}