acoustics/acoustics3d.py¶

Description

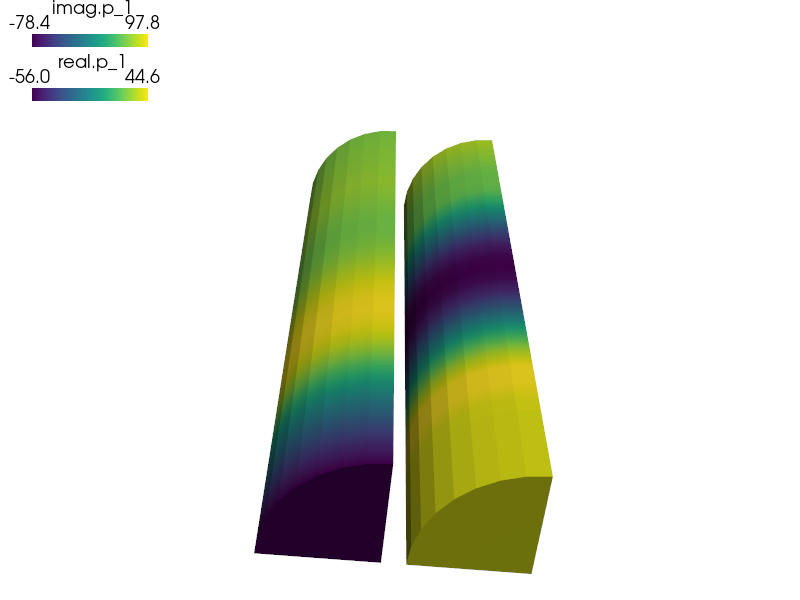
Acoustic pressure distribution in 3D.

Two Laplace equations, one in 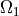$\Omega_1$ , other in 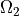$\Omega_2$ , connected on the interface region 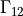$\Gamma_{12}$ using traces of variables.

Find two complex acoustic pressures 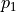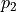$p_1$ , $p_2$ such that:

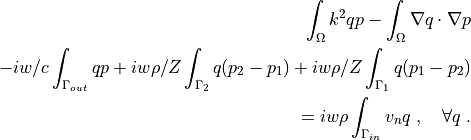
$\int_{\Omega} k^2 q p - \int_{\Omega} \nabla q \cdot \nabla p \\ - i w/c \int_{\Gamma_{out}} q p + i w \rho/Z \int_{\Gamma_2} q (p_2 - p_1) + i w \rho/Z \int_{\Gamma_1} q (p_1 - p_2) \\ = i w \rho \int_{\Gamma_{in}} v_n q \;, \quad \forall q \;.$

../_images/acoustics-acoustics3d_Omega_1.png

../_images/acoustics-acoustics3d_Omega_2.png

source code

r"""
Acoustic pressure distribution in 3D.

Two Laplace equations, one in :math:`\Omega_1`, other in
:math:`\Omega_2`, connected on the interface region :math:`\Gamma_{12}`
using traces of variables.

Find two complex acoustic pressures :math:`p_1`, :math:`p_2` such that:

.. math::
    \int_{\Omega} k^2 q p - \int_{\Omega} \nabla q \cdot \nabla p \\
    - i w/c \int_{\Gamma_{out}} q p
    + i w \rho/Z \int_{\Gamma_2} q (p_2 - p_1)
    + i w \rho/Z \int_{\Gamma_1}  q (p_1 - p_2) \\
    = i w \rho \int_{\Gamma_{in}} v_n q
    \;, \quad \forall q \;.
"""

from __future__ import absolute_import
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/3d/acoustics_mesh3d.mesh'

freq = 1200
v_n = 1.0 # m/s
c = 343.0 # m/s
rho = 1.55 # kg/m^3
R = 1000
w = 2.0 * freq

k1 = w / c
rhoc1 = rho * c

coef_k = ((1.0 + 0.1472 * (freq / R)**(-0.577))
          + 1j * (-0.1734 * (freq / R)**(-0.595)))
coef_r = ((1.0 + 0.0855 * (freq / R)**(-0.754))
          + 1j * (-0.0765 * (freq / R)**(-0.732)))

k2 = k1 * coef_k
rhoc2 = rhoc1 * coef_r

# perforation geometry parameters
tw = 0.9e-3
dh = 2.49e-3
por = 0.08

# acoustic impedance
Z = rho * c / por * (0.006 + 1j * k1 * (tw + 0.375 * dh
                                        * (1 + rhoc2/rhoc1 * k2/k1)))

regions = {
    'Omega' : 'all',
    'Omega_1' : 'cells of group 1',
    'Omega_2' : 'cells of group 2',
    'Gamma_12' : ('r.Omega_1 *v r.Omega_2', 'facet'),
    'Gamma_12_1' : ('copy r.Gamma_12', 'facet', 'Omega_1'),
    'Gamma_12_2' : ('copy r.Gamma_12', 'facet', 'Omega_2'),
    'Gamma_in' : ('vertices in (z < 0.001)', 'facet'),
    'Gamma_out' : ('vertices in (z > 0.157)', 'facet'),
}

materials = {
}

fields = {
    'accoustic_pressure_1' : ('complex', 'scalar', 'Omega_1', 1),
    'accoustic_pressure_2' : ('complex', 'scalar', 'Omega_2', 1),
}

variables = {
    'p_1'   : ('unknown field', 'accoustic_pressure_1'),
    'q_1'   : ('test field',    'accoustic_pressure_1', 'p_1'),
    'p_2'   : ('unknown field', 'accoustic_pressure_2'),
    'q_2'   : ('test field',    'accoustic_pressure_2', 'p_2'),
}

ebcs = {
}

integrals = {
    'i' : 2,
}

equations = {
    'Acoustic pressure' :
    """%s * dw_dot.i.Omega_1(q_1, p_1)
     + %s * dw_dot.i.Omega_2(q_2, p_2)
     - dw_laplace.i.Omega_1(q_1, p_1)
     - dw_laplace.i.Omega_2(q_2, p_2)
     - %s * dw_dot.i.Gamma_out(q_1, p_1)
     + %s * dw_jump.i.Gamma_12_1(q_1, p_1, tr(p_2))
     + %s * dw_jump.i.Gamma_12_2(q_2, p_2, tr(p_1))
     = %s * dw_integrate.i.Gamma_in(q_1)"""
     % (k1*k1, k2*k2,
       1j*k1,
       1j*k1*rhoc1 / Z, 1j*k2*rhoc2 / Z,
       1j*k1*rhoc1 * v_n)
}

options = {
    'nls': 'newton',
    'ls': 'ls',
    'split_results_by': 'region',
    'output_dir': 'output',
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max'      : 1,
        'eps_a'      : 1e-10,
        'eps_r'      : 1.0,
        'macheps'   : 1e-16,
        'lin_red'    : 1e-1,
        'ls_red'     : 0.1,
        'ls_red_warp' : 0.001,
        'ls_on'      : 1.1,
        'ls_min'     : 1e-5,
        'check'     : 0,
        'delta'     : 1e-6,
    })
}