navier_stokes/stokes_slip_bc_penalty.py

Description

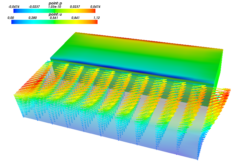
Incompressible Stokes flow with Navier (slip) boundary conditions, flow driven by a moving wall and a small diffusion for stabilization.

This example demonstrates a weak application of no-penetration boundary conditions using the penalty term dw_non_penetration_p.

Find 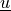, 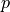such that:

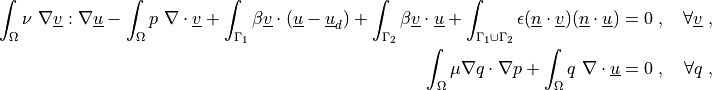
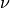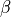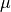where is the fluid viscosity, is the slip coefficient, is the (small) numerical diffusion coefficient, is the penalty coefficient (sufficiently large), 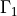is the top wall that moves with the given driving velocity 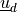and 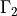are the remaining walls. The Navier conditions are in effect on both 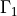, 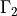and are expressed by the corresponding integrals in the equations above.

The no-penetration boundary conditions are applied on 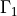, 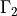. Optionally, Dirichlet boundary conditions can be applied on the inlet, see the code below.

The mesh is created by gen_block_mesh() function - try different mesh dimensions and resolutions below. For large meshes use the 'ls_i' linear solver - PETSc + petsc4py is needed in that case.

See also navier_stokes/stokes_slip_bc.py.

source code

r"""
Incompressible Stokes flow with Navier (slip) boundary conditions, flow driven
by a moving wall and a small diffusion for stabilization.

This example demonstrates a weak application of `no-penetration` boundary
conditions using the penalty term ``dw_non_penetration_p``.

Find :math:`\ul{u}`, :math:`p` such that:

.. math::
    \int_{\Omega} \nu\ \nabla \ul{v} : \nabla \ul{u}
    - \int_{\Omega} p\ \nabla \cdot \ul{v}
    + \int_{\Gamma_1} \beta \ul{v} \cdot (\ul{u} - \ul{u}_d)
    + \int_{\Gamma_2} \beta \ul{v} \cdot \ul{u}
    + \int_{\Gamma_1 \cup \Gamma_2} \epsilon (\ul{n} \cdot \ul{v})
      (\ul{n} \cdot \ul{u})
    = 0
    \;, \quad \forall \ul{v} \;,

    \int_{\Omega} \mu \nabla q \cdot \nabla p
    + \int_{\Omega} q\ \nabla \cdot \ul{u}
    = 0
    \;, \quad \forall q \;,

where :math:`\nu` is the fluid viscosity, :math:`\beta` is the slip
coefficient, :math:`\mu` is the (small) numerical diffusion coefficient,
:math:`\epsilon` is the penalty coefficient (sufficiently large),
:math:`\Gamma_1` is the top wall that moves with the given driving velocity
:math:`\ul{u}_d` and :math:`\Gamma_2` are the remaining walls. The Navier
conditions are in effect on both :math:`\Gamma_1`, :math:`\Gamma_2` and are
expressed by the corresponding integrals in the equations above.

The `no-penetration` boundary conditions are applied on :math:`\Gamma_1`,
:math:`\Gamma_2`. Optionally, Dirichlet boundary conditions can be applied on
the inlet, see the code below.

The mesh is created by ``gen_block_mesh()`` function - try different mesh
dimensions and resolutions below. For large meshes use the ``'ls_i'`` linear
solver - PETSc + petsc4py is needed in that case.

See also :ref:`navier_stokes-stokes_slip_bc`.
"""
from __future__ import absolute_import
import numpy as nm

from sfepy.discrete.fem.meshio import UserMeshIO
from sfepy.mesh.mesh_generators import gen_block_mesh
from sfepy.homogenization.utils import define_box_regions

# Mesh dimensions.
dims = nm.array([3, 1, 0.5])

# Mesh resolution: increase to improve accuracy.
shape = [11, 15, 15]

def mesh_hook(mesh, mode):
    """
    Generate the block mesh.
    """
    if mode == 'read':
        mesh = gen_block_mesh(dims, shape, [0, 0, 0], name='user_block',
                              verbose=False)
        return mesh

    elif mode == 'write':
        pass

filename_mesh = UserMeshIO(mesh_hook)

regions = define_box_regions(3, 0.5 * dims)
regions.update({
    'Omega' : 'all',
    'Gamma1_f' : ('copy r.Top', 'face'),
    'Gamma2_f' : ('r.Near +v r.Bottom +v r.Far', 'face'),
    'Gamma_f' : ('r.Gamma1_f +v r.Gamma2_f', 'face'),
    'Inlet_f' : ('r.Left -v r.Gamma_f', 'face'),
})

fields = {
    'velocity' : ('real', 3, 'Omega', 1),
    'pressure' : ('real', 1, 'Omega', 1),
}

def get_u_d(ts, coors, region=None):
    """
    Given stator velocity.
    """
    out = nm.zeros_like(coors)
    out[:] = [1.0, 1.0, 0.0]

    return out

functions = {
    'get_u_d' : (get_u_d,),
}

variables = {
    'u' : ('unknown field', 'velocity', 0),
    'v' : ('test field',    'velocity', 'u'),
    'u_d' : ('parameter field', 'velocity',
             {'setter' : 'get_u_d'}),
    'p' : ('unknown field', 'pressure', 1),
    'q' : ('test field',    'pressure', 'p'),
}

# Try setting the inlet velocity by un-commenting the 'inlet' ebcs.
ebcs = {
    ## 'inlet' : ('Inlet_f', {'u.0' : 1.0, 'u.[1, 2]' : 0.0}),
}

materials = {
    'm' : ({
        'nu' : 1e-3,
        'beta' : 1e-2,
        'mu' : 1e-10,
        'np_eps' : 1e3,
    },),
}

equations = {
    'balance' :
    """dw_div_grad.5.Omega(m.nu, v, u)
     - dw_stokes.5.Omega(v, p)
     + dw_surface_dot.5.Gamma1_f(m.beta, v, u)
     + dw_surface_dot.5.Gamma2_f(m.beta, v, u)
     + dw_non_penetration_p.5.Gamma1_f(m.np_eps, v, u)
     + dw_non_penetration_p.5.Gamma2_f(m.np_eps, v, u)
     =
     + dw_surface_dot.5.Gamma1_f(m.beta, v, u_d)""",
    'incompressibility' :
    """dw_laplace.5.Omega(m.mu, q, p)
     + dw_stokes.5.Omega(u, q) = 0""",
}

solvers = {
    'ls_d' : ('ls.scipy_direct', {}),
    'ls_i' : ('ls.petsc', {
        'method' : 'bcgsl', # ksp_type
        'precond' : 'bjacobi', # pc_type
        'sub_precond' : 'ilu', # sub_pc_type
        'eps_a' : 0.0, # abstol
        'eps_r' : 1e-12, # rtol
        'eps_d' : 1e10, # Divergence tolerance.
        'i_max' : 1000, # maxits
    }),
    'newton' : ('nls.newton', {
        'i_max' : 1,
        'eps_a'      : 1e-10,
    }),
}

options = {
    'nls' : 'newton',
    'ls' : 'ls_d',
}