linear_elasticity/elastic_shifted_periodic.py¶
Description
Linear elasticity with linear combination constraints and periodic boundary conditions.
The linear combination constraints are used to apply periodic boundary conditions with a shift in the second axis direction.
Find 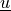 such that:
such that:
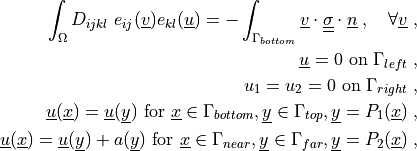
where
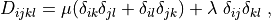
and the traction 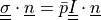 is given in terms of traction pressure
is given in terms of traction pressure 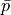 . The function
. The function
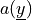 is given (the shift),
is given (the shift), 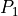 and
and 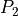 are the
periodic coordinate mappings.
are the
periodic coordinate mappings.
View the results using:
$ ./postproc.py block.vtk --wireframe -b --only-names=u -d'u,plot_displacements,rel_scaling=1,color_kind="scalars",color_name="von_mises_stress"'

r"""
Linear elasticity with linear combination constraints and periodic boundary
conditions.
The linear combination constraints are used to apply periodic boundary
conditions with a shift in the second axis direction.
Find :math:`\ul{u}` such that:
.. math::
\int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
= - \int_{\Gamma_{bottom}} \ul{v} \cdot \ull{\sigma} \cdot \ul{n}
\;, \quad \forall \ul{v} \;,
\ul{u} = 0 \mbox{ on } \Gamma_{left} \;,
u_1 = u_2 = 0 \mbox{ on } \Gamma_{right} \;,
\ul{u}(\ul{x}) = \ul{u}(\ul{y}) \mbox{ for }
\ul{x} \in \Gamma_{bottom}, \ul{y} \in \Gamma_{top},
\ul{y} = P_1(\ul{x}) \;,
\ul{u}(\ul{x}) = \ul{u}(\ul{y}) + a(\ul{y}) \mbox{ for }
\ul{x} \in \Gamma_{near}, \ul{y} \in \Gamma_{far},
\ul{y} = P_2(\ul{x}) \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;,
and the traction :math:`\ull{\sigma} \cdot \ul{n} = \bar{p} \ull{I} \cdot
\ul{n}` is given in terms of traction pressure :math:`\bar{p}`. The function
:math:`a(\ul{y})` is given (the shift), :math:`P_1` and :math:`P_2` are the
periodic coordinate mappings.
View the results using::
$ ./postproc.py block.vtk --wireframe -b --only-names=u -d'u,plot_displacements,rel_scaling=1,color_kind="scalars",color_name="von_mises_stress"'
"""
from __future__ import absolute_import
import numpy as nm
from sfepy.mechanics.matcoefs import stiffness_from_lame
from sfepy.mechanics.tensors import get_von_mises_stress
import sfepy.discrete.fem.periodic as per
from sfepy import data_dir
filename_mesh = data_dir + '/meshes/3d/block.mesh'
options = {
'nls' : 'newton',
'ls' : 'ls',
'post_process_hook' : 'post_process'
}
def post_process(out, pb, state, extend=False):
"""
Calculate and output strain and stress for given displacements.
"""
from sfepy.base.base import Struct
ev = pb.evaluate
stress = ev('ev_cauchy_stress.2.Omega(solid.D, u)', mode='el_avg')
vms = get_von_mises_stress(stress.squeeze())
vms.shape = (vms.shape[0], 1, 1, 1)
out['von_mises_stress'] = Struct(name='output_data', mode='cell',
data=vms, dofs=None)
return out
def linear_tension(ts, coor, mode=None, **kwargs):
if mode == 'qp':
val = 0.1 * nm.sin(coor[:, 0] / 10.)
return {'val' : val.reshape((coor.shape[0], 1, 1))}
def get_shift(ts, coors, region=None):
val = nm.zeros_like(coors, dtype=nm.float64)
val[:, 1] = 0.1 * coors[:, 0]
return val
functions = {
'get_shift' : (get_shift,),
'linear_tension' : (linear_tension,),
'match_y_plane' : (per.match_y_plane,),
'match_z_plane' : (per.match_z_plane,),
}
fields = {
'displacement': ('real', 3, 'Omega', 1),
}
materials = {
'solid' : ({
'D' : stiffness_from_lame(3, lam=5.769, mu=3.846),
},),
'load' : (None, 'linear_tension')
}
variables = {
'u' : ('unknown field', 'displacement', 0),
'v' : ('test field', 'displacement', 'u'),
}
regions = {
'Omega' : 'all',
'Left' : ('vertices in (x < -4.99)', 'facet'),
'Right' : ('vertices in (x > 4.99)', 'facet'),
'Bottom' : ('vertices in (z < -0.99)', 'facet'),
'Top' : ('vertices in (z > 0.99)', 'facet'),
'Near' : ('vertices in (y < -0.99)', 'facet'),
'Far' : ('vertices in (y > 0.99)', 'facet'),
}
ebcs = {
'fix1' : ('Left', {'u.all' : 0.0}),
'fix2' : ('Right', {'u.[1,2]' : 0.0}),
}
epbcs = {
'periodic' : (['Bottom', 'Top'], {'u.all' : 'u.all'}, 'match_z_plane'),
}
lcbcs = {
'shifted' : (('Near', 'Far'),
{'u.all' : 'u.all'},
'match_y_plane', 'shifted_periodic',
'get_shift'),
}
equations = {
'elasticity' : """
dw_lin_elastic.2.Omega(solid.D, v, u)
= -dw_surface_ltr.2.Bottom(load.val, v)
""",
}
solvers = {
'ls' : ('ls.scipy_direct', {}),
'newton' : ('nls.newton', {
'i_max' : 1,
'eps_a' : 1e-10,
}),
}

