sfepy.terms.terms_navier_stokes module¶
- class sfepy.terms.terms_navier_stokes.ConvectTerm(name, arg_str, integral, region, **kwargs)[source]¶
Nonlinear convective term.
- Definition:
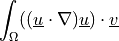
- Call signature:
dw_convect
(virtual, state)- Arguments:
virtual :

state :

- arg_shapes = {'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('virtual', 'state')¶
- static function(out, grad, state, cmap, is_diff)¶
- name = 'dw_convect'¶
- class sfepy.terms.terms_navier_stokes.DivGradTerm(name, arg_str, integral, region, **kwargs)[source]¶
Diffusion term.
- Definition:
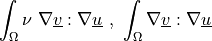
- Call signature:
dw_div_grad
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:
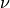 (viscosity, optional)
(viscosity, optional)virtualparameter_1:

state/parameter_2:

- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- static function(out, grad, viscosity, cmap_v, cmap_s, is_diff)¶
- modes = ('weak', 'eval')¶
- name = 'dw_div_grad'¶
- class sfepy.terms.terms_navier_stokes.DivOperatorTerm(name, arg_str, integral, region, **kwargs)[source]¶
Weighted divergence term of a test function.
- Definition:
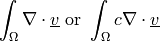
- Call signature:
dw_div
(opt_material, virtual)- Arguments:
material :
 (optional)
(optional)virtual :

- arg_shapes = [{'opt_material': '1, 1', 'virtual': ('D', None)}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'virtual')¶
- name = 'dw_div'¶
- class sfepy.terms.terms_navier_stokes.DivTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate divergence of a vector field.
Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
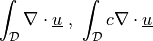
- Call signature:
ev_div
(opt_material, parameter)- Arguments:
parameter :

- arg_shapes = [{'opt_material': '1, 1', 'parameter': 'D'}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'parameter')¶
- integration = ('cell', 'facet_extra')¶
- name = 'ev_div'¶
- class sfepy.terms.terms_navier_stokes.GradDivStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶
Grad-div stabilization term (
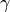 is a global stabilization
parameter).
is a global stabilization
parameter).- Definition:
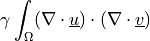
- Call signature:
dw_st_grad_div
(material, virtual, state)- Arguments:
material :
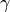
virtual :

state :

- arg_shapes = {'material': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- static function(out, div, coef, cmap, is_diff)¶
- name = 'dw_st_grad_div'¶
- class sfepy.terms.terms_navier_stokes.GradTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate gradient of a scalar or vector field.
Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
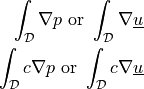
- Call signature:
ev_grad
(opt_material, parameter)- Arguments:
parameter :
 or
or 
- arg_shapes = [{'opt_material': '1, 1', 'parameter': 'N'}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'parameter')¶
- integration = ('cell', 'facet_extra')¶
- name = 'ev_grad'¶
- class sfepy.terms.terms_navier_stokes.LinearConvect2Term(name, arg_str, integral, region, **kwargs)[source]¶
Linearized convective term with the convection velocity given as a material parameter.
- Definition:
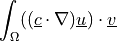
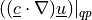
- Call signature:
dw_lin_convect2
(material, virtual, state)- Arguments:
material :
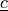
virtual :

state :

- arg_shapes = {'material': 'D, 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- static function(out, grad, state_b, cmap, is_diff)¶
- name = 'dw_lin_convect2'¶
- class sfepy.terms.terms_navier_stokes.LinearConvectTerm(name, arg_str, integral, region, **kwargs)[source]¶
Linearized convective term.
- Definition:
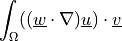
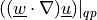
- Call signature:
dw_lin_convect
(virtual, parameter, state)- Arguments:
virtual :

parameter :
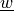
state :

- arg_shapes = {'parameter': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('virtual', 'parameter', 'state')¶
- static function(out, grad, state_b, cmap, is_diff)¶
- name = 'dw_lin_convect'¶
- class sfepy.terms.terms_navier_stokes.PSPGCStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶
PSPG stabilization term, convective part (
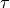 is a local
stabilization parameter).
is a local
stabilization parameter).- Definition:
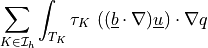
- Call signature:
dw_st_pspg_c
(material, virtual, parameter, state)- Arguments:
material :
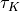
virtual :
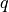
parameter :
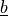
state :

- arg_shapes = {'material': '1, 1', 'parameter': 'D', 'state': 'D', 'virtual': (1, None)}¶
- arg_types = ('material', 'virtual', 'parameter', 'state')¶
- static function(out, state_b, state_u, coef, cmap_p, cmap_u, conn, is_diff)¶
- get_fargs(tau, virtual, parameter, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_st_pspg_c'¶
- class sfepy.terms.terms_navier_stokes.PSPGPStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶
PSPG stabilization term, pressure part (
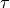 is a local
stabilization parameter), alias to Laplace term dw_laplace.
is a local
stabilization parameter), alias to Laplace term dw_laplace.- Definition:
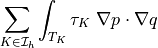
- Call signature:
dw_st_pspg_p
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material :
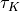
virtual :
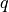
state :

- name = 'dw_st_pspg_p'¶
- class sfepy.terms.terms_navier_stokes.SUPGCStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶
SUPG stabilization term, convective part (
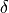 is a local
stabilization parameter).
is a local
stabilization parameter).- Definition:
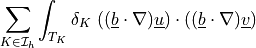
- Call signature:
dw_st_supg_c
(material, virtual, parameter, state)- Arguments:
material :
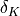
virtual :

parameter :
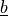
state :

- arg_shapes = {'material': '1, 1', 'parameter': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'parameter', 'state')¶
- static function(out, state_b, state_u, coef, cmap, conn, is_diff)¶
- get_fargs(delta, virtual, parameter, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_st_supg_c'¶
- class sfepy.terms.terms_navier_stokes.SUPGPStabilizationTerm(name, arg_str, integral, region, **kwargs)[source]¶
SUPG stabilization term, pressure part (
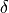 is a local
stabilization parameter).
is a local
stabilization parameter).- Definition:
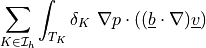
- Call signature:
dw_st_supg_p
(material, virtual, parameter, state)- Arguments:
material :
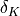
virtual :

parameter :
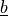
state :

- arg_shapes = {'material': '1, 1', 'parameter': 'D', 'state': 1, 'virtual': ('D', None)}¶
- arg_types = ('material', 'virtual', 'parameter', 'state')¶
- static function(out, state_b, grad_p, coef, cmap_u, cmap_p, is_diff)¶
- get_fargs(delta, virtual, parameter, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- name = 'dw_st_supg_p'¶
- class sfepy.terms.terms_navier_stokes.StokesTerm(name, arg_str, integral, region, **kwargs)[source]¶
Stokes problem coupling term. Corresponds to weak forms of gradient and divergence terms. Can be evaluated.
- Definition:
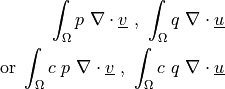
- Call signature:
dw_stokes
(opt_material, virtual, state)(opt_material, state, virtual)(opt_material, parameter_v, parameter_s)- Arguments 1:
material:
 (optional)
(optional)virtual/parameter_v:

state/parameter_s:

- Arguments 2:
material :
 (optional)
(optional)state :

virtual :
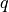
- arg_shapes = [{'opt_material': '1, 1', 'parameter_s': 1, 'parameter_v': 'D', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'state', 'virtual'), ('opt_material', 'parameter_v', 'parameter_s'))¶
- modes = ('grad', 'div', 'eval')¶
- name = 'dw_stokes'¶
- class sfepy.terms.terms_navier_stokes.StokesWaveDivTerm(name, arg_str, integral, region, **kwargs)[source]¶
Stokes dispersion term with the wave vector
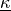 and the
divergence operator.
and the
divergence operator.- Definition:
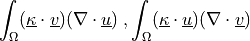
- Call signature:
dw_stokes_wave_div
(material, virtual, state)(material, state, virtual)- Arguments 1:
material :
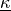
virtual :

state :

- Arguments 2:
material :
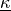
state :

virtual :

- arg_shapes = {'material': '.: D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'))¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- modes = ('kd', 'dk')¶
- name = 'dw_stokes_wave_div'¶
- class sfepy.terms.terms_navier_stokes.StokesWaveTerm(name, arg_str, integral, region, **kwargs)[source]¶
Stokes dispersion term with the wave vector
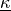 .
.- Definition:
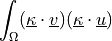
- Call signature:
dw_stokes_wave
(material, virtual, state)- Arguments:
material :
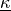
virtual :

statee :

- arg_shapes = {'material': '.: D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- geometries = ['2_3', '2_4', '3_4', '3_8']¶
- name = 'dw_stokes_wave'¶