sfepy.terms.terms_multilinear module¶
- class sfepy.terms.terms_multilinear.ECauchyStressTerm(*args, **kwargs)[source]¶
Evaluate Cauchy stress tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.- Definition:
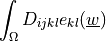
- Call signature:
de_cauchy_stress
(material, parameter)- Arguments:
material :
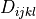
parameter :
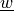
- arg_shapes = {'material': 'S, S', 'parameter': 'D'}¶
- arg_types = ('material', 'parameter')¶
- name = 'de_cauchy_stress'¶
- class sfepy.terms.terms_multilinear.EConvectTerm(*args, **kwargs)[source]¶
Nonlinear convective term.
- Definition:
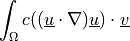
- Call signature:
de_convect
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:
 (optional)
(optional)virtual/parameter_1:

state/parameter_2:

- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_convect'¶
- class sfepy.terms.terms_multilinear.EDiffusionTerm(*args, **kwargs)[source]¶
General diffusion term.
- Definition:
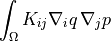
- Call signature:
de_diffusion
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments:
material:
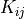
virtual/parameter_1:
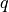
state/parameter_2:

- arg_shapes = {'material': 'D, D', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_diffusion'¶
- class sfepy.terms.terms_multilinear.EDivGradTerm(*args, **kwargs)[source]¶
Vector field diffusion term.
- Definition:
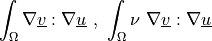
- Call signature:
de_div_grad
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:
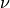 (viscosity, optional)
(viscosity, optional)virtual/parameter_1:

state/parameter_2:

- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_div_grad'¶
- class sfepy.terms.terms_multilinear.EDivTerm(*args, **kwargs)[source]¶
Weighted divergence term.
- Definition:
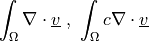
- Call signature:
de_div
(opt_material, virtual)(opt_material, parameter)- Arguments:
material:
 (optional)
(optional)virtual/parameter:

- arg_shapes = [{'opt_material': '1, 1', 'parameter': 'D', 'virtual': ('D', None)}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual'), ('opt_material', 'parameter'))¶
- modes = ('weak', 'eval')¶
- name = 'de_div'¶
- class sfepy.terms.terms_multilinear.EDotTerm(*args, **kwargs)[source]¶
Volume and surface
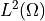 weighted dot product for both
scalar and vector fields. Can be evaluated. Can use derivatives.
weighted dot product for both
scalar and vector fields. Can be evaluated. Can use derivatives.- Definition:
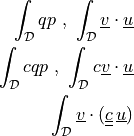
- Call signature:
de_dot
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:
 or
or 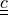 (optional)
(optional)virtual/parameter_1:
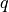 or
or 
state/parameter_2:
 or
or 
- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}, {'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': 'D, D'}, {'opt_material': None}, {'opt_material': '1, 1', 'parameter_1': 'N', 'parameter_2': 'N', 'state': 'N', 'virtual': ('N', 'state')}, {'opt_material': 'N, N'}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- integration = ('cell', 'facet')¶
- modes = ('weak', 'eval')¶
- name = 'de_dot'¶
- class sfepy.terms.terms_multilinear.EGradTerm(*args, **kwargs)[source]¶
Weighted gradient term.
- Definition:
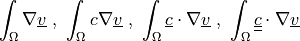
- Call signature:
de_grad
(opt_material, parameter)- Arguments:
material:
 (optional)
(optional)virtual/parameter:

- arg_shapes = [{'opt_material': '1, 1', 'parameter': 'N'}, {'opt_material': 'N, 1'}, {'opt_material': 'N, N'}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'parameter')¶
- name = 'de_grad'¶
- class sfepy.terms.terms_multilinear.EIntegrateOperatorTerm(*args, **kwargs)[source]¶
Volume and surface integral of a test function weighted by a scalar function
 .
.- Definition:
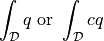
- Call signature:
de_integrate
(opt_material, virtual)- Arguments:
material :
 (optional)
(optional)virtual :
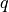
- arg_shapes = [{'opt_material': '1, 1', 'virtual': (1, None)}, {'opt_material': None}]¶
- arg_types = ('opt_material', 'virtual')¶
- integration = ('cell', 'facet')¶
- name = 'de_integrate'¶
- class sfepy.terms.terms_multilinear.ELaplaceTerm(*args, **kwargs)[source]¶
Laplace term with
 coefficient. Can be
evaluated. Can use derivatives.
coefficient. Can be
evaluated. Can use derivatives.- Definition:
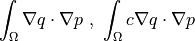
- Call signature:
de_laplace
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:

virtual/parameter_1:
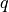
state/parameter_2:

- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 1, 'parameter_2': 1, 'state': 1, 'virtual': (1, 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_laplace'¶
- class sfepy.terms.terms_multilinear.ELinearConvectTerm(*args, **kwargs)[source]¶
Linearized convective term.
- Definition:
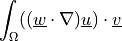
- Call signature:
de_lin_convect
(virtual, parameter, state)(parameter_1, parameter_2, parameter_3)- Arguments:
virtual/parameter_1:

parameter/parameter_2:
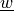
state/parameter_3:

- arg_shapes = {'parameter': 'D', 'parameter_1': 'D', 'parameter_2': 'D', 'parameter_3': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('virtual', 'parameter', 'state'), ('parameter_1', 'parameter_2', 'parameter_3'))¶
- get_function(virtual, parameter, state, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶
- modes = ('weak', 'eval')¶
- name = 'de_lin_convect'¶
- class sfepy.terms.terms_multilinear.ELinearElasticTerm(*args, **kwargs)[source]¶
General linear elasticity term, with
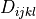 given in
the usual matrix form exploiting symmetry: in 3D it is
given in
the usual matrix form exploiting symmetry: in 3D it is 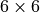 with the indices ordered as
with the indices ordered as ![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in 2D it is
, in 2D it is
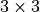 with the indices ordered as
with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.- Definition:
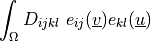
- Call signature:
de_lin_elastic
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments:
material:
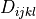
virtual/parameter_1:

state/parameter_2:

- arg_shapes = {'material': 'S, S', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_lin_elastic'¶
- class sfepy.terms.terms_multilinear.ELinearTractionTerm(*args, **kwargs)[source]¶
Linear traction term. The material parameter can have one of the following shapes:
1 or (1, 1) - a given scalar pressure
(D, 1) - a traction vector
(S, 1) or (D, D) - a given stress in symmetric or non-symmetric tensor storage (in symmetric storage indicies are order as follows: 2D: [11, 22, 12], 3D: [11, 22, 33, 12, 13, 23])
- Definition:
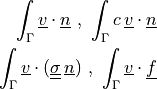
- Call signature:
de_surface_ltr
(opt_material, virtual)(opt_material, parameter)- Arguments:
material:
 ,
, 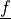 ,
, 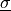 or
or 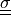
virtual/parameter:

- arg_shapes = [{'opt_material': 'S, 1', 'parameter': 'D', 'virtual': ('D', None)}, {'opt_material': None}, {'opt_material': '1, 1'}, {'opt_material': 'D, 1'}, {'opt_material': 'D, D'}]¶
- arg_types = (('opt_material', 'virtual'), ('opt_material', 'parameter'))¶
- integration = 'facet'¶
- modes = ('weak', 'eval')¶
- name = 'de_surface_ltr'¶
- class sfepy.terms.terms_multilinear.ENonPenetrationPenaltyTerm(*args, **kwargs)[source]¶
Non-penetration condition in the weak sense using a penalty.
- Definition:
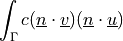
- Call signature:
de_non_penetration_p
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments:
material :

virtual :

state :

- arg_shapes = {'material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- integration = 'facet'¶
- modes = ('weak', 'eval')¶
- name = 'de_non_penetration_p'¶
- class sfepy.terms.terms_multilinear.ENonSymElasticTerm(*args, **kwargs)[source]¶
Elasticity term with non-symmetric gradient. The indices of matrix
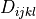 are ordered as
are ordered as
![[11, 12, 13, 21, 22, 23, 31, 32, 33]](../../../_images/math/c7c8170f591e15d2d2117b1e0e7890de0ccb51c9.png) in 3D and as
in 3D and as
![[11, 12, 21, 22]](../../../_images/math/d09e36805a25ebb6c9fbe034ff6223d83d852d5e.png) in 2D.
in 2D.- Definition:
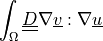
- Call signature:
de_nonsym_elastic
(material, virtual, state)(material, parameter_1, parameter_2)- Arguments:
material:
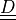
virtual/parameter_1:

state/parameter_2:

- arg_shapes = {'material': 'D2, D2', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('weak', 'eval')¶
- name = 'de_nonsym_elastic'¶
- class sfepy.terms.terms_multilinear.EScalarDotMGradScalarTerm(*args, **kwargs)[source]¶
Volume dot product of a scalar gradient dotted with a material vector with a scalar.
- Definition:
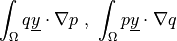
- Call signature:
de_s_dot_mgrad_s
(material, virtual, state)(material, state, virtual)(material, parameter_1, parameter_2)- Arguments 1:
material :
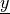
virtual :
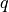
state :

- Arguments 2:
material :
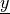
state :

virtual :
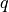
- arg_shapes = [{'material': 'D, 1', 'parameter_1': 1, 'parameter_2': 1, 'state/grad_state': 1, 'state/grad_virtual': 1, 'virtual/grad_state': (1, None), 'virtual/grad_virtual': (1, None)}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_1', 'parameter_2'))¶
- modes = ('grad_state', 'grad_virtual', 'eval')¶
- name = 'de_s_dot_mgrad_s'¶
- class sfepy.terms.terms_multilinear.EStokesTerm(*args, **kwargs)[source]¶
Stokes problem coupling term. Corresponds to weak forms of gradient and divergence terms.
- Definition:
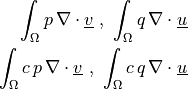
- Call signature:
de_stokes
(opt_material, virtual, state)(opt_material, state, virtual)(opt_material, parameter_v, parameter_s)- Arguments 1:
material:
 (optional)
(optional)virtual/parameter_v:

state/parameter_s:

- Arguments 2:
material :
 (optional)
(optional)state :

virtual :
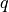
- arg_shapes = [{'opt_material': '1, 1', 'parameter_s': 1, 'parameter_v': 'D', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'state', 'virtual'), ('opt_material', 'parameter_v', 'parameter_s'))¶
- modes = ('grad', 'div', 'eval')¶
- name = 'de_stokes'¶
- class sfepy.terms.terms_multilinear.ETermBase(*args, **kwargs)[source]¶
Reserved letters:
c .. cells q .. quadrature points d-h .. DOFs axes r-z .. auxiliary axes
Layout specification letters:
c .. cells q .. quadrature points v .. variable component - matrix form (v, d) -> vector v*d g .. gradient component d .. local DOF (basis, node) 0 .. all material axes
- can_backend = {'dask_single': <module 'dask.array' from '/home/eldaran/.local/lib/python3.10/site-packages/dask/array/__init__.py'>, 'dask_threads': <module 'dask.array' from '/home/eldaran/.local/lib/python3.10/site-packages/dask/array/__init__.py'>, 'jax': <module 'jax.numpy' from '/home/eldaran/.local/lib/python3.10/site-packages/jax/numpy/__init__.py'>, 'jax_vmap': <module 'jax.numpy' from '/home/eldaran/.local/lib/python3.10/site-packages/jax/numpy/__init__.py'>, 'numpy': <module 'numpy' from '/home/eldaran/.local/lib/python3.10/site-packages/numpy/__init__.py'>, 'numpy_loop': <module 'numpy' from '/home/eldaran/.local/lib/python3.10/site-packages/numpy/__init__.py'>, 'numpy_qloop': <module 'numpy' from '/home/eldaran/.local/lib/python3.10/site-packages/numpy/__init__.py'>, 'opt_einsum': <module 'opt_einsum' from '/home/eldaran/.local/lib/python3.10/site-packages/opt_einsum/__init__.py'>, 'opt_einsum_dask_single': <module 'dask.array' from '/home/eldaran/.local/lib/python3.10/site-packages/dask/array/__init__.py'>, 'opt_einsum_dask_threads': <module 'dask.array' from '/home/eldaran/.local/lib/python3.10/site-packages/dask/array/__init__.py'>, 'opt_einsum_loop': <module 'opt_einsum' from '/home/eldaran/.local/lib/python3.10/site-packages/opt_einsum/__init__.py'>, 'opt_einsum_qloop': <module 'opt_einsum' from '/home/eldaran/.local/lib/python3.10/site-packages/opt_einsum/__init__.py'>}¶
- layout_letters = 'cqgvd0'¶
- verbosity = 0¶
- class sfepy.terms.terms_multilinear.StokesTractionTerm(*args, **kwargs)[source]¶
Surface traction term for Stokes flow problem.
- Definition:
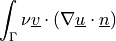
- Call signature:
de_stokes_traction
(opt_material, virtual, state)(opt_material, parameter_1, parameter_2)- Arguments:
material:
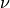 (viscosity, optional)
(viscosity, optional)virtual/parameter_1:

state/parameter_2:

- arg_shapes = [{'opt_material': '1, 1', 'parameter_1': 'D', 'parameter_2': 'D', 'state': 'D', 'virtual': ('D', 'state')}, {'opt_material': None}]¶
- arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'parameter_1', 'parameter_2'))¶
- integration = 'facet_extra'¶
- modes = ('weak', 'eval')¶
- name = 'de_stokes_traction'¶
- class sfepy.terms.terms_multilinear.SurfaceFluxOperatorTerm(*args, **kwargs)[source]¶
Surface flux operator term.
- Definition:
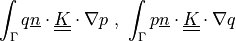
- Call signature:
de_surface_flux
(material, virtual, state)(material, state, virtual)(material, parameter_1, parameter_2)- Arguments 1:
material :
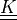
virtual :
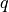
state :

- Arguments 2:
material :
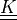
state :

virtual :
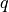
- arg_shapes = [{'material': 'D, D', 'parameter_1': 1, 'parameter_2': 1, 'state/grad_state': 1, 'state/grad_virtual': 1, 'virtual/grad_state': (1, None), 'virtual/grad_virtual': (1, None)}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_1', 'parameter_2'))¶
- integration = 'facet_extra'¶
- modes = ('grad_state', 'grad_virtual', 'eval')¶
- name = 'de_surface_flux'¶
- class sfepy.terms.terms_multilinear.SurfacePiezoFluxOperatorTerm(*args, **kwargs)[source]¶
Surface piezoelectric flux operator term.
Corresponds to the electric flux due to mechanically induced electrical displacement.
- Definition:
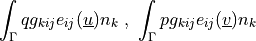
- Call signature:
de_surface_piezo_flux
(material, virtual, state)(material, state, virtual)(material, parameter_1, parameter_2)- Arguments 1:
material :
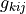
virtual/parameter_1 :
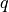
state/parameter_2 :

- Arguments 2:
material :
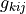
state :

virtual :

- arg_shapes = [{'material': 'D, S', 'parameter_1': 1, 'parameter_2': 'D', 'state/grad_state': 'D', 'state/grad_virtual': 1, 'virtual/grad_state': (1, None), 'virtual/grad_virtual': ('D', None)}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_1', 'parameter_2'))¶
- integration = 'facet_extra'¶
- modes = ('grad_state', 'grad_virtual', 'eval')¶
- name = 'de_surface_piezo_flux'¶
- class sfepy.terms.terms_multilinear.SurfacePiezoFluxTerm(*args, **kwargs)[source]¶
Surface piezoelectric flux term.
Corresponds to the electric flux due to mechanically induced electrical displacement.
- Definition:
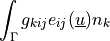
- Call signature:
ev_surface_piezo_flux
(material, parameter)- Arguments 1:
material :
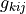
parameter :

- arg_shapes = {'material': 'D, S', 'parameter': 'D'}¶
- arg_types = ('material', 'parameter')¶
- integration = 'facet_extra'¶
- modes = ('eval',)¶
- name = 'ev_surface_piezo_flux'¶