sfepy.terms.terms_contact module¶
- class sfepy.terms.terms_contact.ContactIPCTerm(*args, **kwargs)[source]¶
Contact term based on IPC Toolkit.
This term has a dynamic connectivity of DOFs in its region.
- Definition:
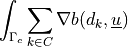
- Call signature:
dw_contact_ipc
(material_m, material_k, material_d, material_p, virtual, state)- Arguments:
material_m :
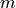
material_k :
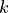
material_d :
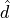
material_p : PSDProjectionMethod
virtual :

state :

- arg_shapes = {'material_d': '.: 1', 'material_k': '.: 1', 'material_m': '.: 1', 'material_p': '.: str', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material_m', 'material_k', 'material_d', 'material_p', 'virtual', 'state')¶
- geometries = ['3_4', '3_8']¶
- get_fargs(avg_mass, stiffness, dhat, spd_projection, virtual, state, mode=None, term_mode=None, diff_var=None, ci=None, **kwargs)[source]¶
- integration = 'facet'¶
- name = 'dw_contact_ipc'¶
- class sfepy.terms.terms_contact.ContactInfo(region, integral, geo, state)[source]¶
Various contact-related data of contact terms.
- class sfepy.terms.terms_contact.ContactTerm(*args, **kwargs)[source]¶
Contact term with a penalty function.
The penalty function is defined as
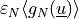 , where
, where 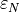 is the normal penalty parameter and
is the normal penalty parameter and
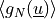 are the Macaulay’s brackets of the gap
function
are the Macaulay’s brackets of the gap
function 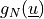 .
.This term has a dynamic connectivity of DOFs in its region.
- Definition:
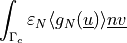
- Call signature:
dw_contact
(material, virtual, state)- Arguments:
material :
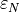
virtual :

state :

- arg_shapes = {'material': '.: 1', 'state': 'D', 'virtual': ('D', 'state')}¶
- arg_types = ('material', 'virtual', 'state')¶
- integration = 'facet'¶
- name = 'dw_contact'¶