sfepy.terms.terms_constraints module¶

class sfepy.terms.terms_constraints.NonPenetrationPenaltyTerm(name, arg_str, integral, region, **kwargs)[source]¶

Non-penetration condition in the weak sense using a penalty.

Definition

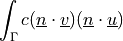
$\int_{\Gamma} c (\ul{n} \cdot \ul{v}) (\ul{n} \cdot \ul{u})$

Call signature

dw_non_penetration_p

(material, virtual, state)

Arguments

material : $c$
virtual : $\ul{v}$
state : $\ul{u}$

arg_shapes = {'material': '1, 1', 'state': 'D', 'virtual': ('D', 'state')}¶

arg_types = ('material', 'virtual', 'state')¶

static function(out, val_qp, ebf, mat, sg, diff_var)[source]¶

get_fargs(mat, vvar, svar, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = 'surface'¶

name = 'dw_non_penetration_p'¶

class sfepy.terms.terms_constraints.NonPenetrationTerm(name, arg_str, integral, region, **kwargs)[source]¶

Non-penetration condition in the weak sense.

Definition

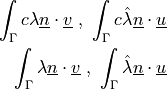
$\int_{\Gamma} c \lambda \ul{n} \cdot \ul{v} \mbox{ , } \int_{\Gamma} c \hat\lambda \ul{n} \cdot \ul{u} \\ \int_{\Gamma} \lambda \ul{n} \cdot \ul{v} \mbox{ , } \int_{\Gamma} \hat\lambda \ul{n} \cdot \ul{u}$

Call signature

dw_non_penetration	`(opt_material, virtual, state)`
	`(opt_material, state, virtual)`

Arguments 1

material : $c$ (optional)
virtual : $\ul{v}$
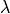
state : $\lambda$

Arguments 2

material : $c$ (optional)
state : $\ul{u}$
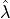
virtual : $\hat\lambda$

arg_shapes = [{'opt_material': '1, 1', 'virtual/grad': ('D', None), 'state/grad': 1, 'virtual/div': (1, None), 'state/div': 'D'}, {'opt_material': None}]¶

arg_types = (('opt_material', 'virtual', 'state'), ('opt_material', 'state', 'virtual'))¶

static function(out, val_qp, ebf, bf, mat, sg, diff_var, mode)[source]¶: ebf belongs to vector variable, bf to scalar variable.

get_fargs(mat, vvar, svar, mode=None, term_mode=None, diff_var=None, **kwargs)[source]¶

integration = 'surface'¶

modes = ('grad', 'div')¶

name = 'dw_non_penetration'¶