sfepy.discrete.fem.lcbc_operators module¶
Operators for enforcing linear combination boundary conditions in nodal FEM setting.
- class sfepy.discrete.fem.lcbc_operators.AverageForceOperator(name, regions, dof_names, dof_map_fun, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for average force multi-point constraint LCBCs.
Unlike in other operators, the regions and dof_names couples are ordered as (independent nodes/DOFs, dependent nodes/DOFs), to allow a simple interchange with the
rigid2LCBC in a problem description. Functionally it corresponds to the RBE3 multi-point constraint in MSC/Nastran.Rotation DOFs in independent nodes are not supported (ignored), see the comment (*) in the code. This is because the independent field is assumed to come from solid elements.
A simplified version for the dependent field without the rotation DOFs is also supported.
- kind = 'average_force'¶
- class sfepy.discrete.fem.lcbc_operators.EdgeDirectionOperator(name, regions, dof_names, dof_map_fun, filename, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for edges direction LCBCs.
The substitution (in 3D) is:
![[u_1, u_2, u_3]^T = [d_1, d_2, d_3]^T w,](../../../../_images/math/d8f05cc74cc10ef8dc116eb3fc3c7bc3ef1094d6.png)
where
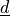 is an edge direction vector averaged into a node. The
new DOF is
is an edge direction vector averaged into a node. The
new DOF is 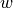 .
.- kind = 'edge_direction'¶
- class sfepy.discrete.fem.lcbc_operators.IntegralMeanValueOperator(name, regions, dof_names, dof_map_fun, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for integral mean value LCBCs. All DOFs in a region are summed to form a single new DOF.
- kind = 'integral_mean_value'¶
- class sfepy.discrete.fem.lcbc_operators.LCBCOperator(name, regions, dof_names, dof_map_fun, variables, functions=None)[source]¶
Base class for LCBC operators.
- class sfepy.discrete.fem.lcbc_operators.LCBCOperators(name, variables, functions=None)[source]¶
Container holding instances of LCBCOperator subclasses for a single variable.
- add_from_bc(bc, ts)[source]¶
Create a new LCBC operator described by bc, and add it to the container.
- Parameters:
- bcLinearCombinationBC instance
The LCBC condition description.
- tsTimeStepper instance
The time stepper.
- finalize()[source]¶
Call this after all LCBCs of the variable have been added.
Initializes the global column indices and DOF counts.
- make_global_operator(adi, new_only=False)[source]¶
Assemble all LCBC operators into a single matrix.
- Parameters:
- adiDofInfo
The active DOF information.
- new_onlybool
If True, the operator columns will contain only new DOFs.
- Returns:
- mtx_lccsr_matrix
The global LCBC operator in the form of a CSR matrix.
- rhs_lcarray
The right-hand side for non-homogeneous LCBCs.
- lcdiDofInfo
The global active LCBC-constrained DOF information.
- class sfepy.discrete.fem.lcbc_operators.MRLCBCOperator(name, regions, dof_names, dof_map_fun, variables, functions=None)[source]¶
Base class for model-reduction type LCBC operators.
These operators are applied to a single field, and replace its DOFs in a given region by new DOFs. In case some field DOFs are to be preserved, those have to be “copied” explicitly, by setting the corresponding row of the operator matrix to a single value one (see, for example,
NoPenetrationOperator).
- class sfepy.discrete.fem.lcbc_operators.MatchDOFsOperator(name, regions, dof_names, dof_map_fun, variables, ts, functions)[source]¶
Transformation matrix operator for match DOFs boundary conditions.
This operator ties DOFs of two fields in two disjoint regions together. It does not create any new DOFs.
- kind = 'match_dofs'¶
- class sfepy.discrete.fem.lcbc_operators.MultiNodeLCOperator(name, regions, dof_names, dof_map_fun, constraints, variables, ts, functions)[source]¶
Transformation matrix operator that defines the DOFs at one (dependent) node as a linear combination of the DOFs at some other (independent) nodes.
The linear combination is given by:

for all
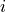 in a given set of DOFs.
in a given set of DOFs. 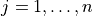 are
the linear constraint indices and
are
the linear constraint indices and  are given weights of
the independent nodes.
are given weights of
the independent nodes.- kind = 'multi_node_combination'¶
- class sfepy.discrete.fem.lcbc_operators.NoPenetrationOperator(name, regions, dof_names, dof_map_fun, filename, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for no-penetration LCBCs.
- kind = 'no_penetration'¶
- class sfepy.discrete.fem.lcbc_operators.NodalLCOperator(name, regions, dof_names, dof_map_fun, constraints, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for the general linear combination of DOFs in each node of a field in the given region.
The DOFs can be fully constrained - then the operator corresponds to enforcing Dirichlet boundary conditions.
The linear combination is given by:
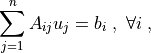
where
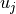 ,
, 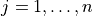 are the DOFs in the node and
are the DOFs in the node and
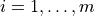 ,
, 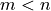 , are the linear constraint indices.
, are the linear constraint indices.SymPy is used to solve the constraint linear system in each node for the dependent DOF(s).
- kind = 'nodal_combination'¶
- class sfepy.discrete.fem.lcbc_operators.NormalDirectionOperator(name, regions, dof_names, dof_map_fun, filename, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for normal direction LCBCs.
The substitution (in 3D) is:
![[u_1, u_2, u_3]^T = [n_1, n_2, n_3]^T w](../../../../_images/math/85c90a747875108b47a06706f2700e770f0d6001.png)
The new DOF is
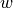 .
.- kind = 'normal_direction'¶
- class sfepy.discrete.fem.lcbc_operators.Rigid2Operator(name, regions, dof_names, dof_map_fun, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for rigid body multi-point constraint LCBCs.
For each dependent node
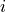 in the first region, its DOFs
in the first region, its DOFs
 are given by the displacement
are given by the displacement  and rotation
and rotation
 in the single independent node in the second region:
in the single independent node in the second region:
where the spin matrix
 is computed using the coordinates
relative to the independent node, i.e.
is computed using the coordinates
relative to the independent node, i.e.  .
Functionally it corresponds to the RBE2 multi-point constraint in
MSC/Nastran.
.
Functionally it corresponds to the RBE2 multi-point constraint in
MSC/Nastran.A simplified version for fields without the rotation DOFs is also supported.
- kind = 'rigid2'¶
- class sfepy.discrete.fem.lcbc_operators.RigidOperator(name, regions, dof_names, dof_map_fun, variables, ts=None, functions=None)[source]¶
Transformation matrix operator for rigid LCBCs.
- kind = 'rigid'¶
- class sfepy.discrete.fem.lcbc_operators.ShiftedPeriodicOperator(name, regions, dof_names, dof_map_fun, shift_fun, variables, ts, functions)[source]¶
Transformation matrix operator for shifted periodic boundary conditions.
This operator ties existing DOFs of two fields in two disjoint regions together. Unlike
MRLCBCOperatorsubclasses, it does not create any new DOFs.- kind = 'shifted_periodic'¶