navier_stokes/stokes.py

Description

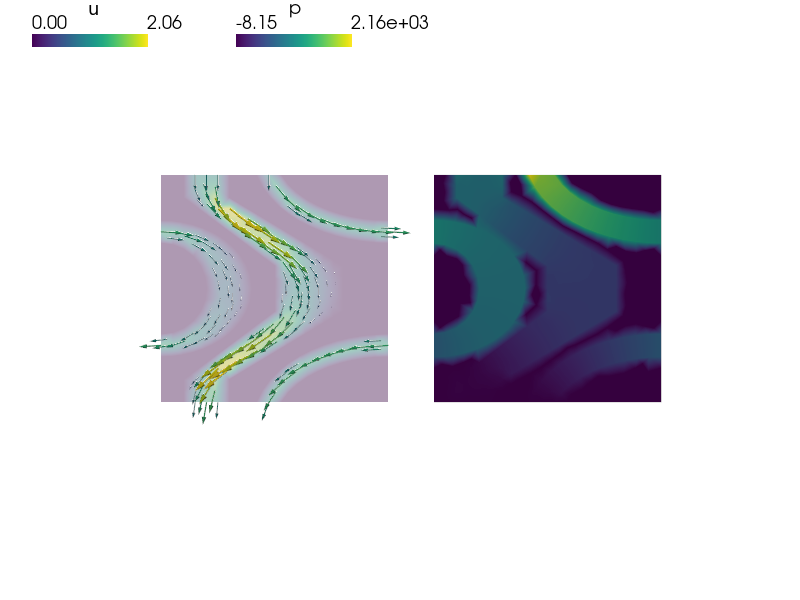
Stokes equations for incompressible fluid flow.

This example demonstrates fields defined on subdomains as well as use of periodic boundary conditions.

Find , such that:

source code

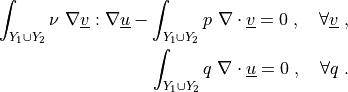
r"""
Stokes equations for incompressible fluid flow.

This example demonstrates fields defined on subdomains as well as use of
periodic boundary conditions.

Find :math:`\ul{u}`, :math:`p` such that:

.. math::
    \int_{Y_1 \cup Y_2} \nu\ \nabla \ul{v} : \nabla \ul{u}
    - \int_{Y_1 \cup Y_2} p\ \nabla \cdot \ul{v}
    = 0
    \;, \quad \forall \ul{v} \;,

    \int_{Y_1 \cup Y_2} q\ \nabla \cdot \ul{u}
    = 0
    \;, \quad \forall q \;.
"""
from __future__ import absolute_import
from sfepy import data_dir
from sfepy.discrete.fem.periodic import match_y_line

filename_mesh = data_dir + '/meshes/2d/special/channels_symm944t.mesh'

if filename_mesh.find( 'symm' ):
    region_1 = {
        'name' : 'Y1',
        'select' : """cells of group 3""",
    }
    region_2 = {
        'name' : 'Y2',
        'select' : """cells of group 4 +c cells of group 6
                      +c cells of group 8""",
    }
    region_4 = {
        'name' : 'Y1Y2',
        'select' : """r.Y1 +c r.Y2""",
    }
    region_5 = {
        'name' : 'Walls',
        'select' : """r.EBCGamma1 +v r.EBCGamma2""",
        'kind' : 'facet',
    }
    region_310 = {
        'name' : 'EBCGamma1',
        'select' : """(cells of group 1 *v cells of group 3)
                      +v
                      (cells of group 2 *v cells of group 3)
                      """,
        'kind' : 'facet',
    }
    region_320 = {
        'name' : 'EBCGamma2',
        'select' : """(cells of group 5 *v cells of group 4)
                      +v
                      (cells of group 1 *v cells of group 4)
                      +v
                      (cells of group 7 *v cells of group 6)
                      +v
                      (cells of group 2 *v cells of group 6)
                      +v
                      (cells of group 9 *v cells of group 8)
                      +v
                      (cells of group 2 *v cells of group 8)
                      """,
        'kind' : 'facet',
    }


w2 = 0.499
# Sides.
region_20 = {
    'name' : 'Left',
    'select' : 'vertices in (x < %.3f)' % -w2,
    'kind' : 'facet',
}
region_21 = {
    'name' : 'Right',
    'select' : 'vertices in (x > %.3f)' % w2,
    'kind' : 'facet',
}
region_22 = {
    'name' : 'Bottom',
    'select' : 'vertices in (y < %.3f)' % -w2,
    'kind' : 'facet',
}
region_23 = {
    'name' : 'Top',
    'select' : 'vertices in (y > %.3f)' % w2,
    'kind' : 'facet',
}

field_1 = {
    'name' : '2_velocity',
    'dtype' : 'real',
    'shape' : (2,),
    'region' : 'Y1Y2',
    'approx_order' : 2,
}

field_2 = {
    'name' : 'pressure',
    'dtype' : 'real',
    'shape' : (1,),
    'region' : 'Y1Y2',
    'approx_order' : 1,
}

variable_1 = {
    'name' : 'u',
    'kind' : 'unknown field',
    'field' : '2_velocity',
    'order' : 0,
}
variable_2 = {
    'name' : 'v',
    'kind' : 'test field',
    'field' : '2_velocity',
    'dual' : 'u',
}
variable_3 = {
    'name' : 'p',
    'kind' : 'unknown field',
    'field' : 'pressure',
    'order' : 1,
}
variable_4 = {
    'name' : 'q',
    'kind' : 'test field',
    'field' : 'pressure',
    'dual' : 'p',
}

integral_1 = {
    'name' : 'i',
    'order' : 2,
}

equations = {
    'balance' :
    """dw_div_grad.i.Y1Y2( fluid.viscosity, v, u )
     - dw_stokes.i.Y1Y2( v, p ) = 0""",
    'incompressibility' :
    """dw_stokes.i.Y1Y2( u, q ) = 0""",
}

material_1 = {
    'name' : 'fluid',
    'values' : {
        'viscosity' : 1.0,
        'density' : 1e0,
    },
}

ebc_1 = {
    'name' : 'walls',
    'region' : 'Walls',
    'dofs' : {'u.all' : 0.0},
}
ebc_2 = {
    'name' : 'top_velocity',
    'region' : 'Top',
    'dofs' : {'u.1' : -1.0, 'u.0' : 0.0},
}
ebc_10 = {
    'name' : 'bottom_pressure',
    'region' : 'Bottom',
    'dofs' : {'p.0' : 0.0},
}

epbc_1 = {
    'name' : 'u_rl',
    'region' : ['Left', 'Right'],
    'dofs' : {'u.all' : 'u.all', 'p.0' : 'p.0'},
    'match' : 'match_y_line',
}

functions = {
    'match_y_line' : (match_y_line,),
}

solver_0 = {
    'name' : 'ls',
    'kind' : 'ls.scipy_direct',
}

solver_1 = {
    'name' : 'newton',
    'kind' : 'nls.newton',

    'i_max'      : 2,
    'eps_a'      : 1e-8,
    'eps_r'      : 1e-2,
    'macheps'   : 1e-16,
    'lin_red'    : 1e-2, # Linear system error < (eps_a * lin_red).
    'ls_red'     : 0.1,
    'ls_red_warp' : 0.001,
    'ls_on'      : 1.1,
    'ls_min'     : 1e-5,
    'check'     : 0,
    'delta'     : 1e-6,
}

save_format = 'hdf5' # 'hdf5' or 'vtk'