navier_stokes/navier_stokes.py

Description

Navier-Stokes equations for incompressible fluid flow.

Find , such that:

source code

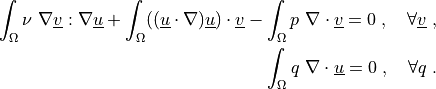
r"""
Navier-Stokes equations for incompressible fluid flow.

Find :math:`\ul{u}`, :math:`p` such that:

.. math::
    \int_{\Omega} \nu\ \nabla \ul{v} : \nabla \ul{u}
    + \int_{\Omega} ((\ul{u} \cdot \nabla) \ul{u}) \cdot \ul{v}
    - \int_{\Omega} p\ \nabla \cdot \ul{v}
    = 0
    \;, \quad \forall \ul{v} \;,

    \int_{\Omega} q\ \nabla \cdot \ul{u}
    = 0
    \;, \quad \forall q \;.
"""
from __future__ import absolute_import
from sfepy import data_dir

filename_mesh = data_dir + '/meshes/3d/elbow2.mesh'

options = {
    'nls' : 'newton',
    'ls' : 'ls',
    'post_process_hook' : 'verify_incompressibility',

    # Options for saving higher-order variables.
    # Possible kinds:
    #    'strip' ... just remove extra DOFs (ignores other linearization
    #                options)
    #    'adaptive' ... adaptively refine linear element mesh.
    'linearization' : {
        'kind' : 'strip',
        'min_level' : 1, # Min. refinement level to achieve everywhere.
        'max_level' : 2, # Max. refinement level.
        'eps' : 1e-1, # Relative error tolerance.
    },
}

field_1 = {
    'name' : '3_velocity',
    'dtype' : 'real',
    'shape' : (3,),
    'region' : 'Omega',
    'approx_order' : '1B',
}

field_2 = {
    'name' : 'pressure',
    'dtype' : 'real',
    'shape' : (1,),
    'region' : 'Omega',
    'approx_order' : 1,
}

# Can use logical operations '&' (and), '|' (or).
region_1000 = {
    'name' : 'Omega',
    'select' : 'cells of group 6',
}

region_0 = {
    'name' : 'Walls',
    'select' : 'vertices of surface -v (r.Outlet +v r.Inlet)',
    'kind' : 'facet',
}
region_1 = {
    'name' : 'Inlet',
    'select' : 'vertices by cinc0', # In
    'kind' : 'facet',
}
region_2 = {
    'name' : 'Outlet',
    'select' : 'vertices by cinc1', # Out
    'kind' : 'facet',
}

ebc_1 = {
    'name' : 'Walls',
    'region' : 'Walls',
    'dofs' : {'u.all' : 0.0},
}
ebc_2 = {
    'name' : 'Inlet',
    'region' : 'Inlet',
    'dofs' : {'u.1' : 1.0, 'u.[0,2]' : 0.0},
}

material_1 = {
    'name' : 'fluid',
    'values' : {
        'viscosity' : 1.25e-3,
        'density' : 1e0,
    },
}

variable_1 = {
    'name' : 'u',
    'kind' : 'unknown field',
    'field' : '3_velocity',
    'order' : 0,
}
variable_2 = {
    'name' : 'v',
    'kind' : 'test field',
    'field' : '3_velocity',
    'dual' : 'u',
}
variable_3 = {
    'name' : 'p',
    'kind' : 'unknown field',
    'field' : 'pressure',
    'order' : 1,
}
variable_4 = {
    'name' : 'q',
    'kind' : 'test field',
    'field' : 'pressure',
    'dual' : 'p',
}
variable_5 = {
    'name' : 'pp',
    'kind' : 'parameter field',
    'field' : 'pressure',
    'like' : 'p',
}

integral_1 = {
    'name' : 'i1',
    'order' : 2,
}
integral_2 = {
    'name' : 'i2',
    'order' : 3,
}

##
# Stationary Navier-Stokes equations.
equations = {
    'balance' :
    """+ dw_div_grad.i2.Omega( fluid.viscosity, v, u )
       + dw_convect.i2.Omega( v, u )
       - dw_stokes.i1.Omega( v, p ) = 0""",
    'incompressibility' :
    """dw_stokes.i1.Omega( u, q ) = 0""",
}

solver_0 = {
    'name' : 'ls',
    'kind' : 'ls.scipy_direct',
}

solver_1 = {
    'name' : 'newton',
    'kind' : 'nls.newton',

    'i_max'      : 5,
    'eps_a'      : 1e-8,
    'eps_r'      : 1.0,
    'macheps'   : 1e-16,
    'lin_red'    : 1e-2, # Linear system error < (eps_a * lin_red).
    'ls_red'     : 0.1,
    'ls_red_warp' : 0.001,
    'ls_on'      : 0.99999,
    'ls_min'     : 1e-5,
    'check'     : 0,
    'delta'     : 1e-6,
}

def verify_incompressibility(out, problem, variables, extend=False):
    """This hook is normally used for post-processing (additional results can
    be inserted into `out` dictionary), but here we just verify the weak
    incompressibility condition."""
    from sfepy.base.base import nm, output, assert_

    one = nm.ones((variables['p'].field.n_nod,), dtype=nm.float64)
    variables.set_state_parts({'p' : one})
    zero = problem.evaluate('dw_stokes.i1.Omega(u, p)')
    output('div(u) = %.3e' % zero)

    assert_(abs(zero) < 1e-14)

    return out

##
# Functions.
import os.path as op
import sys

sys.path.append(data_dir) # Make installed example work.
import sfepy.examples.navier_stokes.utils as utils

cinc_name = 'cinc_' + op.splitext(op.basename(filename_mesh))[0]
cinc = getattr(utils, cinc_name)

functions = {
    'cinc0' : (lambda coors, domain=None: cinc(coors, 0),),
    'cinc1' : (lambda coors, domain=None: cinc(coors, 1),),
}