linear_elasticity/wedge_mesh.py

Description

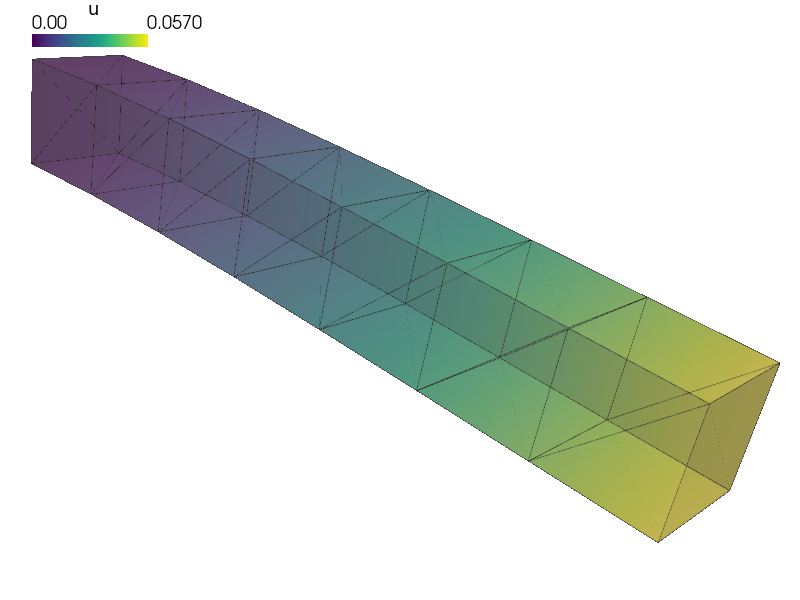
A linear elastic beam loaded with a continuous force. The FE meshes consisting of hexehedral, tetrahedral, and wedge elements are used in the simulation and the results are compared.

The displacement at the beam end is compared to the reference solution calculated on the homogeneous hexahedral mesh.

Running the simulation:

sfepy-run sfepy/examples/linear_elasticity/wedge_mesh.py

Viewing the results:

sfepy-view output/beam_h7.vtk output/beam_t42.vtk output/beam_w14.vtk -f u:s0:wu:e:p0 u:s1:wu:e:p0 u:s2:wu:e:p0 --camera-position="1.2,-0.6,0.1,0.4,0.1,-0.1,-0.2,0.1,1"

source code

r"""
A linear elastic beam loaded with a continuous force. The FE meshes consisting
of hexehedral, tetrahedral, and wedge elements are used in the simulation and
the results are compared.

The displacement at the beam end is compared to the reference
solution calculated on the homogeneous hexahedral mesh.

Running the simulation::

    sfepy-run sfepy/examples/linear_elasticity/wedge_mesh.py

Viewing the results::

    sfepy-view output/beam_h7.vtk output/beam_t42.vtk output/beam_w14.vtk -f u:s0:wu:e:p0 u:s1:wu:e:p0 u:s2:wu:e:p0 --camera-position="1.2,-0.6,0.1,0.4,0.1,-0.1,-0.2,0.1,1"
"""
import os.path as osp
import numpy as nm
from sfepy import data_dir
from sfepy.mechanics.matcoefs import stiffness_from_youngpoisson
from sfepy.base.base import Struct
from sfepy.discrete import Problem
from sfepy.discrete.fem import Mesh
from sfepy.discrete.fem.meshio import UserMeshIO
from scipy.spatial.transform import Rotation

global_dict = {}


def mesh_hook(mesh, mode):
    if mode == 'read' and 'mesh_hook_param' in global_dict:
        fname, angle = global_dict['mesh_hook_param']
        mesh = Mesh.from_file(fname)

        center = nm.average(mesh.cmesh.coors, axis=0)
        coors = mesh.cmesh.coors - center

        rot = Rotation.from_rotvec(nm.array([1., 0, 0]) * nm.deg2rad(angle))
        mesh.cmesh.coors[:] = rot.apply(coors) + center

        return mesh


def test_meshes(pb0):
    out = []
    conf = pb0.conf.copy()
    ok = True

    for mesh_group in meshes:
        displ = []
        for mesh in mesh_group:
            if isinstance(mesh, tuple):
                fname = osp.join(data_dir, 'meshes', '3d', mesh[0])
                angle = mesh[1]
                global_dict['mesh_hook_param'] = (fname, angle)
                conf.filename_mesh = UserMeshIO(mesh_hook)
            else:
                conf.filename_mesh = osp.join(data_dir, 'meshes', '3d', mesh)

            pb = Problem.from_conf(conf)
            pb.set_output_dir(pb0.output_dir)

            yield pb, out

            displ.append(out[-1][1]['u'].data[-1].reshape((-1, 3)))

            yield None

        err = nm.array([d[-1, 2] - displ[0][-1, 2] for d in displ[1:]]) < 0.01
        ok = ok and err.all()

    print(f'wedge elements test: {["failed!", "passed"][int(ok)]}')


def get_force(ts, coors, mode=None, **kwargs):
    if mode == 'qp':
        force = 1e3

        val = nm.zeros_like(coors)[..., None]
        val[:, 2, 0] = -coors[:, 0] / 0.7 * force

        return {'val': val}


def post_proces(out, pb, state, extend=False):
    S = pb.evaluate('ev_cauchy_stress.i.Omega(solid.D, u)', mode='el_avg')
    out['stress'] = Struct(name='out', data=S, mode='cell')

    return out


meshes = [
    ['beam_h7.mesh', ('beam_w14.vtk', 90), ('beam_w14.vtk', 270)],
    ['beam_t42.mesh', 'beam_w14.vtk', ('beam_w14.vtk', 180)],
]

def define():
    filename_mesh = osp.join(data_dir, 'meshes', '3d', meshes[0][0])

    options = {
        'post_process_hook': 'post_proces',
        'parametric_hook': 'test_meshes',
        'output_dir': 'output',
    }

    regions = {
        'Omega': 'all',
        'Left': ('vertices in (x < 0.01)', 'facet'),
        'Right': ('vertices in (x > 0.69)', 'facet'),
        'Top': ('vertices in (z > 0.09)', 'facet'),
        'Bottom': ('vertices in (z < 0.01)', 'facet'),
        'Edge': ('r.Bottom *v r.Right', 'vertex'),
    }

    functions = {
        'get_force' : (get_force,),
    }

    materials = {
        'solid': ({'D': stiffness_from_youngpoisson(dim=3, young=1e6,
                                                    poisson=0.3)},),
        'force': 'get_force',
    }

    fields = {
        'displacement': ('real', 'vector', 'Omega', 1),
    }

    integrals = {
        'i': 2,
    }

    variables = {
        'u': ('unknown field', 'displacement', 0),
        'v': ('test field', 'displacement', 'u'),
    }

    ebcs = {
        'Fixed': ('Left', {'u.all' : 0.0}),
    }

    equations = {
        'balance_of_forces':
        """dw_lin_elastic.i.Omega(solid.D, v, u)
        = dw_surface_ltr.i.Top(force.val, v)"""
    }

    solvers = {
        'ls': ('ls.auto_direct', {}),
        'newton': ('nls.newton', {
            'i_max': 1,
            'eps_a': 1e-6,
        }),
    }

    return locals()