linear_elasticity/shell10x_cantilever.py

Description

Bending of a long thin cantilever beam, declarative problem description.

The example demonstrates use of the dw_shell10x term.

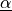Find displacements of the central plane , and rotations such that:

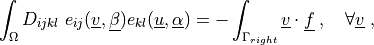
where 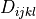is the isotropic elastic tensor, given using the Young’s modulus 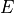and the Poisson’s ratio .

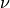The variable u below holds both and 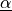DOFs. For visualization, it is saved as two fields u_disp and u_rot, corresponding to and 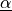, respectively.

See also linear_elasticity/shell10x_cantilever_interactive.py example.

View the results using:

sfepy-view shell10x.vtk -f u_disp:wu_disp 1:vw

source code

r"""
Bending of a long thin cantilever beam, declarative problem description.

The example demonstrates use of the
:class:`dw_shell10x <sfepy.terms.terms_shells.Shell10XTerm>` term.

Find displacements of the central plane :math:`\ul{u}`, and rotations
:math:`\ul{\alpha}` such that:

.. math::
    \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}, \ul{\beta})
    e_{kl}(\ul{u}, \ul{\alpha})
    = - \int_{\Gamma_{right}} \ul{v} \cdot \ul{f}
    \;, \quad \forall \ul{v} \;,

where :math:`D_{ijkl}` is the isotropic elastic tensor, given using the Young's
modulus :math:`E` and the Poisson's ratio :math:`\nu`.

The variable ``u`` below holds both :math:`\ul{u}` and :math:`\ul{\alpha}`
DOFs. For visualization, it is saved as two fields ``u_disp`` and ``u_rot``,
corresponding to :math:`\ul{u}` and :math:`\ul{\alpha}`, respectively.

See also :ref:`linear_elasticity-shell10x_cantilever_interactive` example.

View the results using::

  sfepy-view shell10x.vtk -f u_disp:wu_disp 1:vw
"""
from __future__ import absolute_import
from sfepy.base.base import output
from sfepy.discrete.fem.meshio import UserMeshIO
from sfepy.discrete import Integral
import sfepy.mechanics.shell10x as sh

import sfepy.examples.linear_elasticity.shell10x_cantilever_interactive as sci

# Beam dimensions.
dims = [0.2, 0.01, 0.001]
thickness = dims[2]

transform = 'bend' # None, 'bend' or 'twist'

# Mesh resolution: increase to improve accuracy.
shape = [11, 2]

# Material parameters.
young = 210e9
poisson = 0.3

# Loading force.
force = -1.0

def mesh_hook(mesh, mode):
    """
    Generate the beam mesh.
    """
    if mode == 'read':
        mesh = sci.make_mesh(dims[:2], shape, transform=transform)
        return mesh

def post_process(out, problem, state, extend=False):
    u = problem.get_variables()['u']
    gamma2 = problem.domain.regions['Gamma2']

    dofs = u.get_state_in_region(gamma2)
    output('DOFs along the loaded edge:')
    output('\n%s' % dofs)

    if transform != 'twist':
        label, ii = {None : ('u_3', 2), 'bend' : ('u_1', 0)}[transform]

        u_exact = sci.get_analytical_displacement(dims, young, force,
                                                  transform=transform)
        output('max. %s displacement:' % label, dofs[0, ii])
        output('analytical value:', u_exact)

    return out

filename_mesh = UserMeshIO(mesh_hook)

options = {
    'nls' : 'newton',
    'ls' : 'ls',
    'post_process_hook' : 'post_process',
}

if transform is None:
    pload = [[0.0, 0.0, force / shape[1], 0.0, 0.0, 0.0]] * shape[1]

elif transform == 'bend':
    pload = [[force / shape[1], 0.0, 0.0, 0.0, 0.0, 0.0]] * shape[1]

elif transform == 'twist':
    pload = [[0.0, force / shape[1], 0.0, 0.0, 0.0, 0.0]] * shape[1]

materials = {
    'm' : ({
            'D' : sh.create_elastic_tensor(young=young, poisson=poisson),
            '.drill' : 1e-7,
    },),
    'load' : ({
            '.val' : pload,
    },)
}

xmin = (-0.5 + 1e-12) * dims[0]
xmax = (0.5 - 1e-12) * dims[0]

regions = {
    'Omega' : 'all',
    'Gamma1' : ('vertices in (x < %.14f)' % xmin, 'facet'),
    'Gamma2' : ('vertices in (x > %.14f)' % xmax, 'facet'),
}

fields = {
    'fu': ('real', 6, 'Omega', 1, 'H1', 'shell10x'),
}

variables = {
    'u' : ('unknown field', 'fu', 0),
    'v' : ('test field', 'fu', 'u'),
}

ebcs = {
    'fix' : ('Gamma1', {'u.all' : 0.0}),
}

# Custom integral.
aux = Integral('i', order=3)
qp_coors, qp_weights = aux.get_qp('3_8')
qp_coors[:, 2] = thickness * (qp_coors[:, 2] - 0.5)
qp_weights *= thickness

integrals = {
    'i' : ('custom', qp_coors, qp_weights),
}

equations = {
    'elasticity' :
    """dw_shell10x.i.Omega(m.D, m.drill, v, u)
     = dw_point_load.i.Gamma2(load.val, v)""",
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max'      : 1,
        'eps_a'      : 1e-7,
    }),
}