linear_elasticity/linear_elastic_damping.py¶
Description
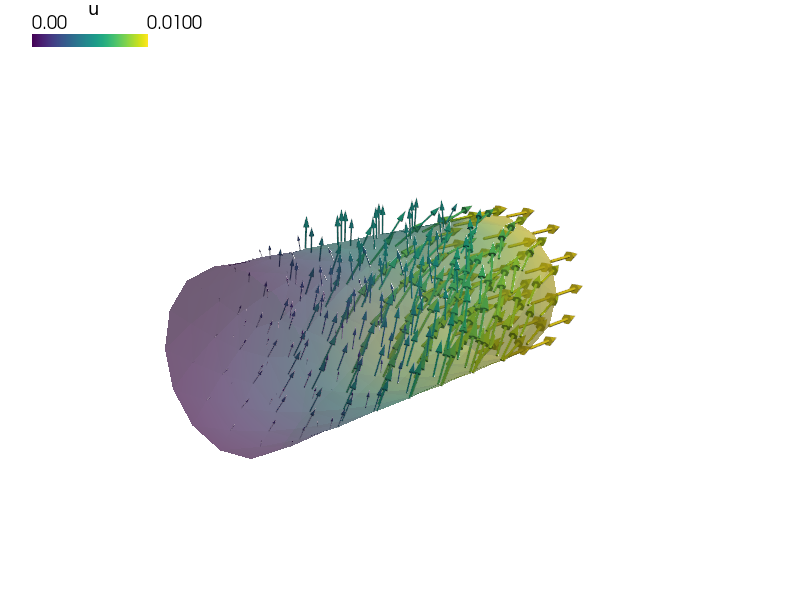
Time-dependent linear elasticity with a simple damping.
Find  such that:
such that:
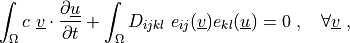
where
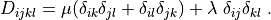
r"""
Time-dependent linear elasticity with a simple damping.
Find :math:`\ul{u}` such that:
.. math::
\int_{\Omega} c\ \ul{v} \cdot \pdiff{\ul{u}}{t}
+ \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
= 0
\;, \quad \forall \ul{v} \;,
where
.. math::
D_{ijkl} = \mu (\delta_{ik} \delta_{jl}+\delta_{il} \delta_{jk}) +
\lambda \ \delta_{ij} \delta_{kl}
\;.
"""
from copy import deepcopy
import numpy as nm
from sfepy.examples.linear_elasticity.linear_elastic import \
filename_mesh, materials, regions, fields, ebcs, \
integrals, solvers
def print_times(problem, state):
print(nm.array(problem.ts.times))
options = {
'ts' : 'ts',
'save_times' : 'all',
'post_process_hook_final' : print_times,
'output_format' : 'h5',
}
variables = {
'u' : ('unknown field', 'displacement', 0, 1),
'v' : ('test field', 'displacement', 'u'),
}
# Put density to 'solid'.
materials = deepcopy(materials)
materials['solid'][0].update({'c' : 1000.0})
# Moving the PerturbedSurface region.
ebcs = deepcopy(ebcs)
ebcs['PerturbedSurface'][1].update({'u.0' : 'ebc_sin'})
def ebc_sin(ts, coors, **kwargs):
val = 0.01 * nm.sin(2.0*nm.pi*ts.nt)
return nm.tile(val, (coors.shape[0],))
equations = {
'balance_of_forces in time' :
"""dw_dot.i.Omega( solid.c, v, du/dt )
+ dw_lin_elastic.i.Omega( solid.D, v, u ) = 0""",
}
def adapt_time_step(ts, status, adt, problem, verbose=False):
if ts.time > 0.5:
ts.set_time_step(0.1)
return True
solvers = deepcopy(solvers) # Do not spoil linear_elastic.py namespace in tests.
solvers.update({
'ts' : ('ts.adaptive', {
't0' : 0.0,
't1' : 1.0,
'dt' : None,
'n_step' : 101,
'adapt_fun' : adapt_time_step,
'verbose' : 1,
}),
})
ls = solvers['ls']
ls[1].update({'use_presolve' : True})
functions = {
'ebc_sin' : (ebc_sin,),
}