linear_elasticity/elastic_contact_sphere.py

Description

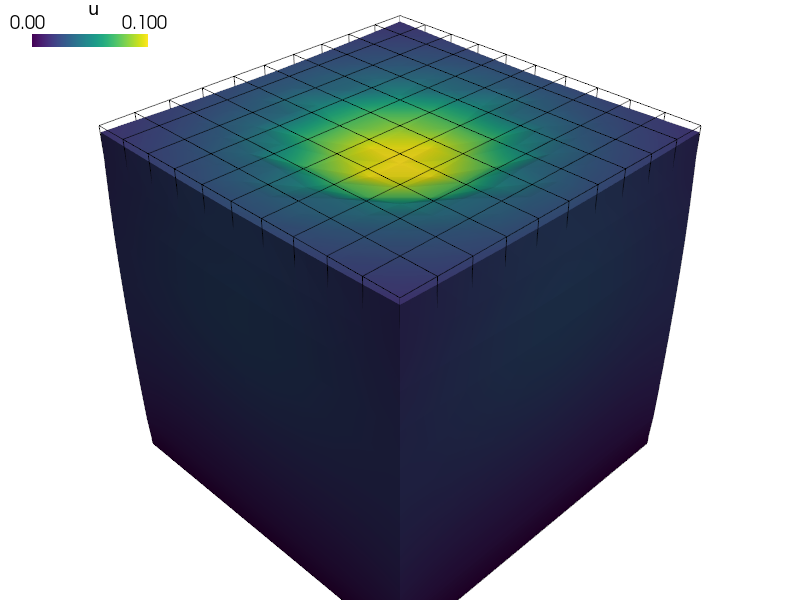
Elastic contact sphere simulating an indentation test.

Find such that:

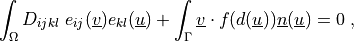
where

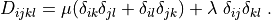
Notes

Even though the material is linear elastic and small deformations are used, the problem is highly nonlinear due to contacts with the sphere. See also elastic_contact_planes.py example.

source code

r"""
Elastic contact sphere simulating an indentation test.

Find :math:`\ul{u}` such that:

.. math::
    \int_{\Omega} D_{ijkl}\ e_{ij}(\ul{v}) e_{kl}(\ul{u})
    + \int_{\Gamma} \ul{v} \cdot f(d(\ul{u})) \ul{n}(\ul{u})
    = 0 \;,

where

.. math::
    D_{ijkl} = \mu (\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}) +
    \lambda \ \delta_{ij} \delta_{kl}
    \;.

Notes
-----

Even though the material is linear elastic and small deformations are used, the
problem is highly nonlinear due to contacts with the sphere. See also
elastic_contact_planes.py example.
"""
from __future__ import absolute_import
from sfepy import data_dir
from sfepy.mechanics.matcoefs import stiffness_from_lame

filename_mesh = data_dir + '/meshes/3d/cube_medium_hexa.mesh'

k = 1e5 # Elastic sphere stiffness for positive penetration.
f0 = 1e-2 # Force at zero penetration.

options = {
    'nls' : 'newton',
    'ls' : 'ls',

    'output_format': 'vtk',
}

fields = {
    'displacement': ('real', 3, 'Omega', 1),
}

materials = {
    'solid' : ({
        'D': stiffness_from_lame(dim=3, lam=5.769, mu=3.846),
    },),
    'cs' : ({
        'f' : [k, f0],
        '.c' : [0.0, 0.0, 1.2],
        '.r' : 0.8,
    },),
}

variables = {
    'u' : ('unknown field', 'displacement', 0),
    'v' : ('test field', 'displacement', 'u'),
}

regions = {
    'Omega' : 'all',
    'Bottom' : ('vertices in (z < -0.499)', 'facet'),
    'Top' : ('vertices in (z > 0.499)', 'facet'),
}

ebcs = {
    'fixed' : ('Bottom', {'u.all' : 0.0}),
}

equations = {
    'elasticity' :
    """dw_lin_elastic.2.Omega(solid.D, v, u)
     + dw_contact_sphere.2.Top(cs.f, cs.c, cs.r, v, u)
     = 0""",
}

solvers = {
    'ls' : ('ls.scipy_direct', {}),
    'newton' : ('nls.newton', {
        'i_max' : 20,
        'eps_a' : 1e-1,
        'ls_on' : 2.0,
        'check' : 0,
        'delta' : 1e-6,
    }),
}

def main():
    import os

    import numpy as nm
    import matplotlib.pyplot as plt

    from sfepy.discrete.fem import MeshIO
    import sfepy.linalg as la
    from sfepy.mechanics.contact_bodies import ContactSphere, plot_points

    conf_dir = os.path.dirname(__file__)
    io = MeshIO.any_from_filename(filename_mesh, prefix_dir=conf_dir)
    bb = io.read_bounding_box()
    outline = [vv for vv in la.combine(zip(*bb))]

    ax = plot_points(None, nm.array(outline), 'r*')
    csc = materials['cs'][0]
    cs = ContactSphere(csc['.c'], csc['.r'])

    pps = (bb[1] - bb[0]) * nm.random.rand(5000, 3) + bb[0]
    mask = cs.mask_points(pps, 0.0)

    ax = plot_points(ax, cs.centre[None, :], 'b*', ms=30)
    ax = plot_points(ax, pps[mask], 'kv')
    ax = plot_points(ax, pps[~mask], 'r.')

    plt.show()

if __name__ == '__main__':
    main()