homogenization/nonlinear_hyperelastic_mM.py¶
Description
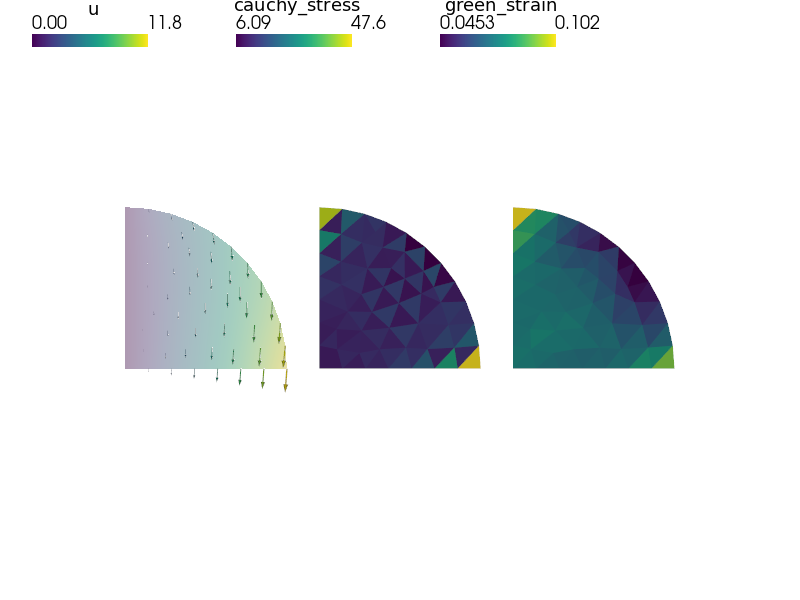
Homogenized nonlinear hyperelastic material with evolving microstructure deformation in each macroscopic quadrature point.
Run in parallel using:
mpiexec -n 4 sfepy-run --app=bvp-mM --debug-mpi sfepy/examples/homogenization/nonlinear_hyperelastic_mM.py
"""
Homogenized nonlinear hyperelastic material with evolving microstructure
deformation in each macroscopic quadrature point.
Run in parallel using::
mpiexec -n 4 sfepy-run --app=bvp-mM --debug-mpi sfepy/examples/homogenization/nonlinear_hyperelastic_mM.py
"""
import numpy as nm
from sfepy import data_dir, base_dir
from sfepy.base.base import Struct, output
from sfepy.terms.terms_hyperelastic_ul import HyperElasticULFamilyData
from sfepy.homogenization.micmac import get_homog_coefs_nonlinear
import sfepy.linalg as la
from sfepy.discrete.evaluate import Evaluator
hyperelastic_data = {}
def post_process(out, pb, state, extend=False):
if isinstance(state, dict):
pass
else:
pb.update_materials_flag = 2
stress = pb.evaluate('ev_integrate_mat.1.Omega(solid.S, u)',
mode='el_avg')
out['cauchy_stress'] = Struct(name='output_data',
mode='cell',
data=stress,
dofs=None)
strain = pb.evaluate('ev_integrate_mat.1.Omega(solid.E, u)',
mode='el_avg')
out['green_strain'] = Struct(name='output_data',
mode='cell',
data=strain,
dofs=None)
pb.update_materials_flag = 0
if pb.conf.options.get('recover_micro', False):
happ = pb.homogen_app
if pb.ts.step == 0:
rname = pb.conf.options.recovery_region
rcells = pb.domain.regions[rname].get_cells()
sh = hyperelastic_data['homog_mat_shape']
happ.app_options.store_micro_idxs = sh[1] * rcells
else:
hpb = happ.problem
recovery_hook = hpb.conf.options.get('recovery_hook', None)
if recovery_hook is not None:
recovery_hook = hpb.conf.get_function(recovery_hook)
rname = pb.conf.options.recovery_region
rcoors = []
for ii in happ.app_options.store_micro_idxs:
key = happ.get_micro_cache_key('coors', ii, pb.ts.step)
if key in happ.micro_state_cache:
rcoors.append(happ.micro_state_cache[key])
recovery_hook(hpb, rcoors, pb.domain.regions[rname], pb.ts)
return out
def get_homog_mat(ts, coors, mode, term=None, problem=None, **kwargs):
if problem.update_materials_flag == 2 and mode == 'qp':
out = hyperelastic_data['homog_mat']
return {k: nm.array(v) for k, v in out.items()}
elif problem.update_materials_flag == 0 or not mode == 'qp':
return
output('get_homog_mat')
dim = problem.domain.mesh.dim
update_var = problem.conf.options.mesh_update_variables[0]
state_u = problem.equations.variables[update_var]
state_u.field.clear_mappings()
family_data = problem.family_data(state_u, term.region, term.integral,
term.geometry_types['u'])
mtx_f = family_data.mtx_f.reshape((coors.shape[0],)
+ family_data.mtx_f.shape[-2:])
if hasattr(problem, 'mtx_f_prev'):
rel_mtx_f = la.dot_sequences(mtx_f, nm.linalg.inv(problem.mtx_f_prev),
'AB')
else:
rel_mtx_f = mtx_f
problem.mtx_f_prev = mtx_f.copy()
macro_data = {'mtx_e': rel_mtx_f - nm.eye(dim)} # '*' - macro strain
out = get_homog_coefs_nonlinear(ts, coors, mode, macro_data,
term=term, problem=problem,
iteration=problem.iiter, **kwargs)
out['E'] = 0.5 * (la.dot_sequences(mtx_f, mtx_f, 'ATB') - nm.eye(dim))
hyperelastic_data['time'] = ts.step
hyperelastic_data['homog_mat_shape'] = family_data.det_f.shape[:2]
hyperelastic_data['homog_mat'] = \
{k: nm.array(v) for k, v in out.items()}
return out
def ulf_iteration_hook(pb, nls, vec, it, err, err0):
Evaluator.new_ulf_iteration(pb, nls, vec, it, err, err0)
pb.iiter = it
pb.update_materials_flag = True
pb.update_materials()
pb.update_materials_flag = False
class MyEvaluator(Evaluator):
def eval_residual(self, vec, is_full=False):
if not is_full:
vec = self.problem.equations.make_full_vec(vec)
vec_r = self.problem.equations.eval_residuals(vec * 0)
return vec_r
def ulf_init(pb):
pb.family_data = HyperElasticULFamilyData()
pb_vars = pb.get_variables()
pb_vars['u'].init_data()
pb.update_materials_flag = True
pb.iiter = 0
options = {
'output_dir': 'output',
'mesh_update_variables': ['u'],
'nls_iter_hook': ulf_iteration_hook,
'pre_process_hook': ulf_init,
'micro_filename': (base_dir +
'/examples/homogenization/nonlinear_homogenization.py'),
'recover_micro': True,
'recovery_region': 'Recovery',
'post_process_hook': post_process,
'user_evaluator': MyEvaluator,
}
materials = {
'solid': 'get_homog',
}
fields = {
'displacement': ('real', 'vector', 'Omega', 1),
}
variables = {
'u': ('unknown field', 'displacement'),
'v': ('test field', 'displacement', 'u'),
}
filename_mesh = data_dir + '/meshes/2d/its2D.mesh'
regions = {
'Omega': 'all',
'Left': ('vertices in (x < 0.001)', 'facet'),
'Bottom': ('vertices in (y < 0.001 )', 'facet'),
'Recovery': ('cell 49, 81', 'cell'),
}
ebcs = {
'l': ('Left', {'u.all': 0.0}),
'b': ('Bottom', {'u.all': 'move_bottom'}),
}
centre = nm.array([0, 0], dtype=nm.float64)
def move_bottom(ts, coor, **kwargs):
from sfepy.linalg import rotation_matrix2d
vec = coor[:, 0:2] - centre
angle = 3 * ts.step
print('angle:', angle)
mtx = rotation_matrix2d(angle)
out = nm.dot(vec, mtx) - vec
return out
functions = {
'move_bottom': (move_bottom,),
'get_homog': (get_homog_mat,),
}
equations = {
'balance_of_forces':
"""dw_nonsym_elastic.1.Omega(solid.A, v, u)
= - dw_lin_prestress.1.Omega(solid.S, v)""",
}
solvers = {
'ls': ('ls.scipy_direct', {}),
'newton': ('nls.newton', {
'eps_a': 1e-3,
'eps_r': 1e-3,
'i_max': 20,
}),
'ts': ('ts.simple', {
't0': 0,
't1': 1,
'n_step': 3 + 1,
'verbose': 1,
})
}