diffusion/time_poisson_interactive.py¶
Description
Transient Laplace equation (heat equation) with non-constant initial conditions given by a function, using commands for interactive use.
The script allows setting various simulation parameters, namely:
the diffusivity coefficient
the max. initial condition value
temperature field approximation order
uniform mesh refinement
The example shows also how to probe the results.
In the SfePy top-level directory the following command can be used to get usage information:
python sfepy/examples/diffusion/time_poisson_interactive.py -h
#!/usr/bin/env python
"""
Transient Laplace equation (heat equation) with non-constant initial conditions
given by a function, using commands for interactive use.
The script allows setting various simulation parameters, namely:
- the diffusivity coefficient
- the max. initial condition value
- temperature field approximation order
- uniform mesh refinement
The example shows also how to probe the results.
In the SfePy top-level directory the following command can be used to get usage
information::
python sfepy/examples/diffusion/time_poisson_interactive.py -h
"""
import sys
sys.path.append('.')
from argparse import ArgumentParser, RawDescriptionHelpFormatter
import numpy as nm
import matplotlib.pyplot as plt
from sfepy.base.base import assert_, output, ordered_iteritems, IndexedStruct
from sfepy.discrete import (FieldVariable, Material, Integral, Function,
Equation, Equations, Problem)
from sfepy.discrete.problem import prepare_matrix
from sfepy.discrete.fem import Mesh, FEDomain, Field
from sfepy.terms import Term
from sfepy.discrete.conditions import Conditions, EssentialBC, InitialCondition
from sfepy.solvers.ls import ScipyDirect
from sfepy.solvers.nls import Newton
from sfepy.solvers.ts_solvers import SimpleTimeSteppingSolver
from sfepy.discrete.probes import LineProbe, CircleProbe
from sfepy.discrete.projections import project_by_component
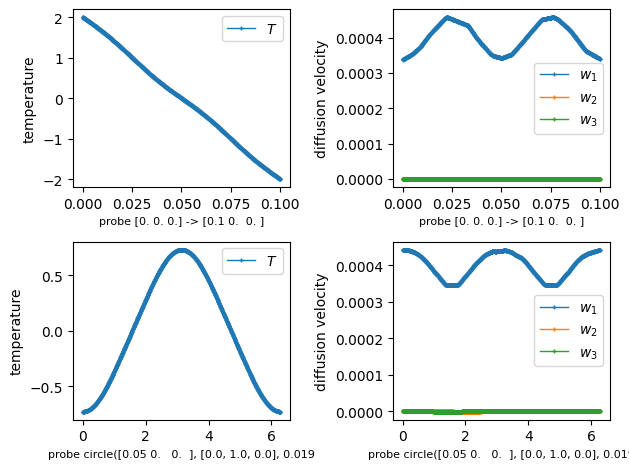
def gen_probes(problem):
"""
Define a line probe and a circle probe.
"""
# Use enough points for higher order approximations.
n_point = 1000
p0, p1 = nm.array([0.0, 0.0, 0.0]), nm.array([0.1, 0.0, 0.0])
line = LineProbe(p0, p1, n_point, share_geometry=True)
# Workaround current probe code shortcoming.
line.set_options(close_limit=0.5)
centre = 0.5 * (p0 + p1)
normal = [0.0, 1.0, 0.0]
r = 0.019
circle = CircleProbe(centre, normal, r, n_point, share_geometry=True)
circle.set_options(close_limit=0.0)
probes = [line, circle]
labels = ['%s -> %s' % (p0, p1),
'circle(%s, %s, %s' % (centre, normal, r)]
return probes, labels
def probe_results(ax_num, T, dvel, probe, label):
"""
Probe the results using the given probe and plot the probed values.
"""
results = {}
pars, vals = probe(T)
results['T'] = (pars, vals)
pars, vals = probe(dvel)
results['dvel'] = (pars, vals)
fig = plt.figure(1)
ax = plt.subplot(2, 2, 2 * ax_num + 1)
ax.cla()
pars, vals = results['T']
ax.plot(pars, vals[:, 0], label=r'$T$', lw=1, ls='-', marker='+', ms=3)
dx = 0.05 * (pars[-1] - pars[0])
ax.set_xlim(pars[0] - dx, pars[-1] + dx)
ax.set_ylabel('temperature')
ax.set_xlabel('probe %s' % label, fontsize=8)
ax.legend(loc='best', fontsize=10)
ax = plt.subplot(2, 2, 2 * ax_num + 2)
ax.cla()
pars, vals = results['dvel']
for ic in range(vals.shape[1]):
ax.plot(pars, vals[:, ic], label=r'$w_{%d}$' % (ic + 1),
lw=1, ls='-', marker='+', ms=3)
dx = 0.05 * (pars[-1] - pars[0])
ax.set_xlim(pars[0] - dx, pars[-1] + dx)
ax.set_ylabel('diffusion velocity')
ax.set_xlabel('probe %s' % label, fontsize=8)
ax.legend(loc='best', fontsize=10)
return fig, results
helps = {
'diffusivity' : 'the diffusivity coefficient [default: %(default)s]',
'ic_max' : 'the max. initial condition value [default: %(default)s]',
'order' : 'temperature field approximation order [default: %(default)s]',
'refine' : 'uniform mesh refinement level [default: %(default)s]',
'probe' : 'probe the results',
'show' : 'show the probing results figure, if --probe is used',
}
def main():
from sfepy import data_dir
parser = ArgumentParser(description=__doc__,
formatter_class=RawDescriptionHelpFormatter)
parser.add_argument('--version', action='version', version='%(prog)s')
parser.add_argument('--diffusivity', metavar='float', type=float,
action='store', dest='diffusivity',
default=1e-5, help=helps['diffusivity'])
parser.add_argument('--ic-max', metavar='float', type=float,
action='store', dest='ic_max',
default=2.0, help=helps['ic_max'])
parser.add_argument('--order', metavar='int', type=int,
action='store', dest='order',
default=2, help=helps['order'])
parser.add_argument('-r', '--refine', metavar='int', type=int,
action='store', dest='refine',
default=0, help=helps['refine'])
parser.add_argument('-p', '--probe',
action="store_true", dest='probe',
default=False, help=helps['probe'])
parser.add_argument('-s', '--show',
action="store_true", dest='show',
default=False, help=helps['show'])
options = parser.parse_args()
assert_((0 < options.order),
'temperature approximation order must be at least 1!')
output('using values:')
output(' diffusivity:', options.diffusivity)
output(' max. IC value:', options.ic_max)
output('uniform mesh refinement level:', options.refine)
mesh = Mesh.from_file(data_dir + '/meshes/3d/cylinder.mesh')
domain = FEDomain('domain', mesh)
if options.refine > 0:
for ii in range(options.refine):
output('refine %d...' % ii)
domain = domain.refine()
output('... %d nodes %d elements'
% (domain.shape.n_nod, domain.shape.n_el))
omega = domain.create_region('Omega', 'all')
left = domain.create_region('Left',
'vertices in x < 0.00001', 'facet')
right = domain.create_region('Right',
'vertices in x > 0.099999', 'facet')
field = Field.from_args('fu', nm.float64, 'scalar', omega,
approx_order=options.order)
T = FieldVariable('T', 'unknown', field, history=1)
s = FieldVariable('s', 'test', field, primary_var_name='T')
m = Material('m', diffusivity=options.diffusivity * nm.eye(3))
integral = Integral('i', order=2*options.order)
t1 = Term.new('dw_diffusion(m.diffusivity, s, T)',
integral, omega, m=m, s=s, T=T)
t2 = Term.new('dw_dot(s, dT/dt)',
integral, omega, s=s, T=T)
eq = Equation('balance', t1 + t2)
eqs = Equations([eq])
# Boundary conditions.
ebc1 = EssentialBC('T1', left, {'T.0' : 2.0})
ebc2 = EssentialBC('T2', right, {'T.0' : -2.0})
# Initial conditions.
def get_ic(coors, ic):
x, y, z = coors.T
return 2 - 40.0 * x + options.ic_max * nm.sin(4 * nm.pi * x / 0.1)
ic_fun = Function('ic_fun', get_ic)
ic = InitialCondition('ic', omega, {'T.0' : ic_fun})
pb = Problem('heat', equations=eqs)
pb.set_bcs(ebcs=Conditions([ebc1, ebc2]))
pb.set_ics(Conditions([ic]))
variables = pb.get_initial_state()
init_fun, prestep_fun, _poststep_fun = pb.get_tss_functions()
ls = ScipyDirect({})
nls_status = IndexedStruct()
nls = Newton({'is_linear' : True}, lin_solver=ls, status=nls_status)
tss = SimpleTimeSteppingSolver({'t0' : 0.0, 't1' : 100.0, 'n_step' : 11},
nls=nls, context=pb, verbose=True)
pb.set_solver(tss)
if options.probe:
# Prepare probe data.
probes, labels = gen_probes(pb)
ev = pb.evaluate
order = 2 * (options.order - 1)
gfield = Field.from_args('gu', nm.float64, 'vector', omega,
approx_order=options.order - 1)
dvel = FieldVariable('dvel', 'parameter', gfield,
primary_var_name='(set-to-None)')
cfield = Field.from_args('gu', nm.float64, 'scalar', omega,
approx_order=options.order - 1)
component = FieldVariable('component', 'parameter', cfield,
primary_var_name='(set-to-None)')
nls_options = {'eps_a' : 1e-16, 'i_max' : 1}
suffix = tss.ts.suffix
def poststep_fun(ts, vec):
vec = _poststep_fun(ts, vec)
# Probe the solution.
dvel_qp = ev('ev_diffusion_velocity.%d.Omega(m.diffusivity, T)'
% order, copy_materials=False, mode='qp')
project_by_component(dvel, dvel_qp, component, order,
nls_options=nls_options)
all_results = []
for ii, probe in enumerate(probes):
fig, results = probe_results(ii, T, dvel, probe, labels[ii])
all_results.append(results)
plt.tight_layout()
fig.savefig('time_poisson_interactive_probe_%s.png'
% (suffix % ts.step), bbox_inches='tight')
for ii, results in enumerate(all_results):
output('probe %d (%s):' % (ii, probes[ii].name))
output.level += 2
for key, res in ordered_iteritems(results):
output(key + ':')
val = res[1]
output(' min: %+.2e, mean: %+.2e, max: %+.2e'
% (val.min(), val.mean(), val.max()))
output.level -= 2
return vec
else:
poststep_fun = _poststep_fun
pb.time_update(tss.ts)
variables.apply_ebc()
# This is required if {'is_linear' : True} is passed to Newton.
mtx = prepare_matrix(pb, variables)
pb.try_presolve(mtx)
tss_status = IndexedStruct()
tss(variables.get_state(pb.active_only, force=True),
init_fun=init_fun, prestep_fun=prestep_fun, poststep_fun=poststep_fun,
status=tss_status)
output(tss_status)
if options.show:
plt.show()
if __name__ == '__main__':
main()