diffusion/time_poisson.py¶
Description
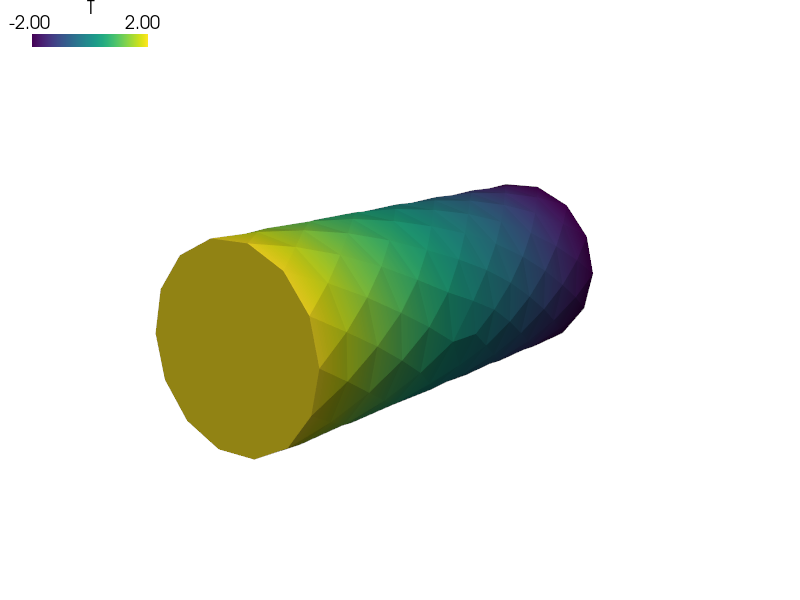
Transient Laplace equation with non-constant initial conditions given by a function.
Find 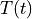 for
for ![t \in [0, t_{\rm final}]](../_images/math/9f80775f131863202ea25954249a43c09294920c.png) such that:
such that:
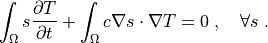
r"""
Transient Laplace equation with non-constant initial conditions given by a
function.
Find :math:`T(t)` for :math:`t \in [0, t_{\rm final}]` such that:
.. math::
\int_{\Omega} s \pdiff{T}{t}
+ \int_{\Omega} c \nabla s \cdot \nabla T
= 0
\;, \quad \forall s \;.
"""
from sfepy import data_dir
filename_mesh = data_dir + '/meshes/3d/cylinder.mesh'
t0 = 0.0
t1 = 0.1
n_step = 11
material_2 = {
'name' : 'coef',
'values' : {'val' : 0.01},
'kind' : 'stationary', # 'stationary' or 'time-dependent'
}
field_1 = {
'name' : 'temperature',
'dtype' : 'real',
'shape' : (1,),
'region' : 'Omega',
'approx_order' : 1,
}
variable_1 = {
'name' : 'T',
'kind' : 'unknown field',
'field' : 'temperature',
'order' : 0,
'history' : 1,
}
variable_2 = {
'name' : 's',
'kind' : 'test field',
'field' : 'temperature',
'dual' : 'T',
}
regions = {
'Omega' : 'all',
'Gamma_Left' : ('vertices in (x < 0.00001)', 'facet'),
'Gamma_Right' : ('vertices in (x > 0.099999)', 'facet'),
}
ebcs = {
'T1': ('Gamma_Left', {'T.0' : 2.0}),
'T2': ('Gamma_Right', {'T.0' : -2.0}),
}
def get_ic(coor, ic):
"""Non-constant initial condition."""
import numpy as nm
# Normalize x coordinate.
mi, ma = coor[:,0].min(), coor[:,0].max()
nx = (coor[:,0] - mi) / (ma - mi)
return nm.where( (nx > 0.25) & (nx < 0.75 ), 8.0 * (nx - 0.5), 0.0 )
functions = {
'get_ic' : (get_ic,),
}
ics = {
'ic' : ('Omega', {'T.0' : 'get_ic'}),
}
integral_1 = {
'name' : 'i',
'order' : 1,
}
equations = {
'Temperature' :
"""dw_dot.i.Omega( s, dT/dt )
+ dw_laplace.i.Omega( coef.val, s, T ) = 0"""
}
solver_0 = {
'name' : 'ls',
'kind' : 'ls.scipy_direct',
'use_presolve' : True,
}
solver_1 = {
'name' : 'newton',
'kind' : 'nls.newton',
'i_max' : 1,
'eps_a' : 1e-10,
'eps_r' : 1.0,
'macheps' : 1e-16,
'lin_red' : 1e-2, # Linear system error < (eps_a * lin_red).
'ls_red' : 0.1,
'ls_red_warp' : 0.001,
'ls_on' : 1.1,
'ls_min' : 1e-5,
'check' : 0,
'delta' : 1e-6,
'is_linear' : True,
}
solver_2 = {
'name' : 'ts',
'kind' : 'ts.simple',
't0' : t0,
't1' : t1,
'dt' : None,
'n_step' : n_step, # has precedence over dt!
'verbose' : 1,
}
options = {
'nls' : 'newton',
'ls' : 'ls',
'ts' : 'ts',
'save_times' : 'all',
}