dg/advection_1D.py

Description

Transient advection equation in 1D solved using discontinous galerkin method.

Usage Examples

Run:

sfepy-run sfepy/examples/dg/advection_1D.py

To view animated results use sfepy/examples/dg/dg_plot_1D.py specifing name of the output in output/ folder, default is dg/advection_1D:

python3 sfepy/examples/dg/dg_plot_1D.py dg/advection_1D

dg_plot_1D.py also accepts full and relative paths:

python3 sfepy/examples/dg/dg_plot_1D.py output/dg/advection_1D

source code

r"""
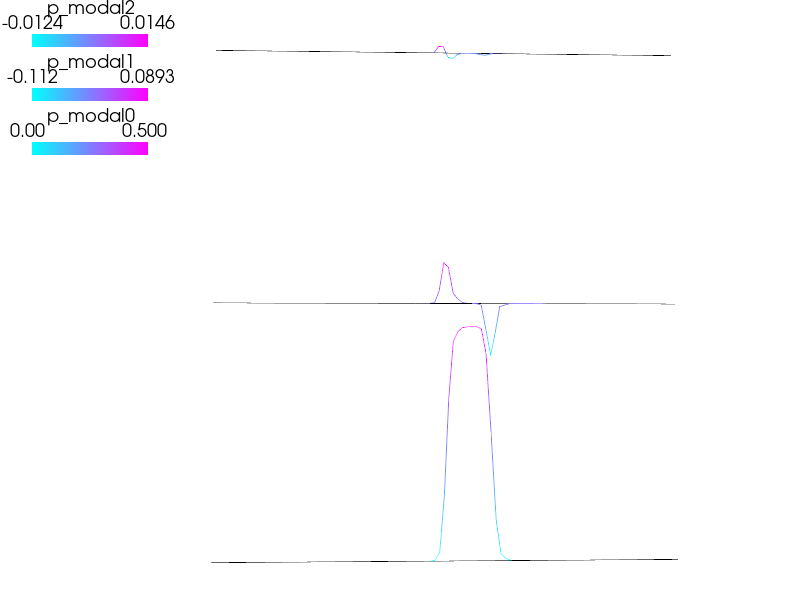
Transient advection equation in 1D solved using discontinous galerkin method.

.. math:: \frac{dp}{dt} + a \cdot dp/dx = 0

    p(t,0) = p(t,1)


Usage Examples
--------------
Run::

  sfepy-run sfepy/examples/dg/advection_1D.py

To view animated results use ``sfepy/examples/dg/dg_plot_1D.py`` specifing name
of the output in ``output/`` folder, default is ``dg/advection_1D``::

  python3 sfepy/examples/dg/dg_plot_1D.py dg/advection_1D

``dg_plot_1D.py`` also accepts full and relative paths::

  python3 sfepy/examples/dg/dg_plot_1D.py output/dg/advection_1D
"""
from sfepy.examples.dg.example_dg_common import *
from sfepy.discrete.dg.limiters import MomentLimiter1D

dim = 1

def define(filename_mesh=None,
           approx_order=2,

           adflux=0.0,
           limit=True,

           cw=None,
           diffcoef=None,
           diffscheme="symmetric",

           cfl=0.4,
           dt=None,
           t1=0.1
           ):

    t0 = 0
    transient = True

    mstart = 0
    mend = 1

    diffcoef = None
    cw = None

    example_name = "advection_1D"
    dim = 1

    if filename_mesh is None:
        filename_mesh = get_gen_1D_mesh_hook(0, 1, 100)

    materials = {
        'a': ({'val': [1.0], '.flux': adflux},),

    }

    regions = {
        'Omega': 'all',
        'Gamma': ('vertices of surface', 'facet'),
        'left': ('vertices in x == 0', 'vertex'),
        'right': ('vertices in x == 1', 'vertex')
    }

    fields = {
        'f': ('real', 'scalar', 'Omega', str(approx_order) + 'd', 'DG', 'legendre')
    }

    variables = {
        'p': ('unknown field', 'f', 0, 1),
        'v': ('test field', 'f', 'p'),
    }

    dgebcs = {
        'u_left': ('left', {'p.all': 0}),
        'u_righ': ('right', {'p.all': 0}),
    }

    dgepbc_1 = {
        'name'  : 'u_rl',
        'region': ['right', 'left'],
        'dofs': {'p.all': 'p.all'},
        'match': 'match_y_line',
    }

    integrals = {
        'i': 2 * approx_order,
    }

    equations = {
        'Advection': """
                       dw_dot.i.Omega(v, p)
                       - dw_s_dot_mgrad_s.i.Omega(a.val, p[-1], v)
                       + dw_dg_advect_laxfrie_flux.i.Omega(a.flux, a.val, v, p[-1]) = 0
                      """
    }

    solvers = {
        "tss": ('ts.tvd_runge_kutta_3',
                {"t0"     : t0,
                 "t1"     : t1,
                 'limiters': {"f": MomentLimiter1D} if limit else {}
                 }),
        'nls': ('nls.newton', {}),
        'ls' : ('ls.scipy_direct', {})
    }

    options = {
        'ts'              : 'tss',
        'nls'             : 'newton',
        'ls'              : 'ls',
        'save_times'      : 100,
        'active_only'     : False,
        'pre_process_hook': get_cfl_setup(cfl)
                            if dt is None else
                            get_cfl_setup(dt=dt),
        'output_dir'      : 'output/dg/' + example_name,
        'output_format'   : "vtk",
    }


    functions = {}

    def local_register_function(fun):
        try:
            functions.update({fun.__name__: (fun,)})

        except AttributeError:  # Already a sfepy Function.
            fun = fun.function
            functions.update({fun.__name__: (fun,)})

        return fun

    def four_step_p(x):
        """
        piecewise constant (-inf, 1.8],(1.8, a + 4](a+4, a + 5](a + 5, inf)
        """
        return nm.piecewise(x,
                            [x <= mstart,
                             x <= mstart + .4,
                             mstart + .4 < x,
                             mstart + .5 <= x],
                            [0, 0, .5, 0])

    @local_register_function
    def get_ic(x, ic=None):
        return four_step_p(x)

    def analytic_sol(coors, t=None, uset=False):
        x = coors[..., 0]
        if uset:
            res = get_ic(x[..., None] - t[None, ...])
            return res # for animating transient problem

        res = get_ic(x[..., None])
        return res[..., 0]

    @local_register_function
    def sol_fun(ts, coors, mode="qp", **kwargs):
        t = ts.time
        if mode == "qp":
            return {"p": analytic_sol(coors, t)[..., None, None]}

    ics = {
        'ic': ('Omega', {'p.0': 'get_ic'}),
    }

    return locals()