diffusion/poisson_parallel_interactive.py¶
Description
Parallel assembling and solving of a Poisson’s equation, using commands for interactive use.
Find 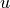 such that:
such that:
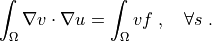
Important Notes¶
This example requires petsc4py, mpi4py and (optionally) pymetis with their dependencies installed!
This example generates a number of files - do not use an existing non-empty directory for the
output_dirargument.Use the
--clearoption with care!
Notes¶
Each task is responsible for a subdomain consisting of a set of cells (a cell region).
Each subdomain owns PETSc DOFs within a consecutive range.
When both global and task-local variables exist, the task-local variables have
_isuffix.This example does not use a nonlinear solver.
This example can serve as a template for solving a linear single-field scalar problem - just replace the equations in
create_local_problem().The command line options are saved into <output_dir>/options.txt file.
Usage Examples¶
See all options:
$ python examples/diffusion/poisson_parallel_interactive.py -h
See PETSc options:
$ python examples/diffusion/poisson_parallel_interactive.py -help
Single process run useful for debugging with debug():
$ python examples/diffusion/poisson_parallel_interactive.py output-parallel
Parallel runs:
$ mpiexec -n 3 python examples/diffusion/poisson_parallel_interactive.py output-parallel -2 --shape=101,101
$ mpiexec -n 3 python examples/diffusion/poisson_parallel_interactive.py output-parallel -2 --shape=101,101 --metis
$ mpiexec -n 5 python examples/diffusion/poisson_parallel_interactive.py output-parallel -2 --shape=101,101 --verify --metis -ksp_monitor -ksp_converged_reason
View the results using:
$ python postproc.py output-parallel/sol.h5 --wireframe -b -d'u,plot_warp_scalar'
#!/usr/bin/env python
r"""
Parallel assembling and solving of a Poisson's equation, using commands for
interactive use.
Find :math:`u` such that:
.. math::
\int_{\Omega} \nabla v \cdot \nabla u
= \int_{\Omega} v f
\;, \quad \forall s \;.
Important Notes
---------------
- This example requires petsc4py, mpi4py and (optionally) pymetis with their
dependencies installed!
- This example generates a number of files - do not use an existing non-empty
directory for the ``output_dir`` argument.
- Use the ``--clear`` option with care!
Notes
-----
- Each task is responsible for a subdomain consisting of a set of cells (a cell
region).
- Each subdomain owns PETSc DOFs within a consecutive range.
- When both global and task-local variables exist, the task-local
variables have ``_i`` suffix.
- This example does not use a nonlinear solver.
- This example can serve as a template for solving a linear single-field scalar
problem - just replace the equations in :func:`create_local_problem()`.
- The command line options are saved into <output_dir>/options.txt file.
Usage Examples
--------------
See all options::
$ python examples/diffusion/poisson_parallel_interactive.py -h
See PETSc options::
$ python examples/diffusion/poisson_parallel_interactive.py -help
Single process run useful for debugging with :func:`debug()
<sfepy.base.base.debug>`::
$ python examples/diffusion/poisson_parallel_interactive.py output-parallel
Parallel runs::
$ mpiexec -n 3 python examples/diffusion/poisson_parallel_interactive.py output-parallel -2 --shape=101,101
$ mpiexec -n 3 python examples/diffusion/poisson_parallel_interactive.py output-parallel -2 --shape=101,101 --metis
$ mpiexec -n 5 python examples/diffusion/poisson_parallel_interactive.py output-parallel -2 --shape=101,101 --verify --metis -ksp_monitor -ksp_converged_reason
View the results using::
$ python postproc.py output-parallel/sol.h5 --wireframe -b -d'u,plot_warp_scalar'
"""
from __future__ import absolute_import
from argparse import RawDescriptionHelpFormatter, ArgumentParser
import os
import sys
sys.path.append('.')
import csv
import numpy as nm
import matplotlib.pyplot as plt
from sfepy.base.base import output, Struct
from sfepy.base.ioutils import ensure_path, remove_files_patterns, save_options
from sfepy.base.timing import Timer
from sfepy.discrete.fem import Mesh, FEDomain, Field
from sfepy.discrete.common.region import Region
from sfepy.discrete import (FieldVariable, Material, Integral, Function,
Equation, Equations, Problem, State)
from sfepy.discrete.conditions import Conditions, EssentialBC
from sfepy.discrete.evaluate import apply_ebc_to_matrix
from sfepy.terms import Term
from sfepy.solvers.ls import PETScKrylovSolver
import sfepy.parallel.parallel as pl
import sfepy.parallel.plot_parallel_dofs as ppd
def create_local_problem(omega_gi, order):
"""
Local problem definition using a domain corresponding to the global region
`omega_gi`.
"""
mesh = omega_gi.domain.mesh
# All tasks have the whole mesh.
bbox = mesh.get_bounding_box()
min_x, max_x = bbox[:, 0]
eps_x = 1e-8 * (max_x - min_x)
mesh_i = Mesh.from_region(omega_gi, mesh, localize=True)
domain_i = FEDomain('domain_i', mesh_i)
omega_i = domain_i.create_region('Omega', 'all')
gamma1_i = domain_i.create_region('Gamma1',
'vertices in (x < %.10f)'
% (min_x + eps_x),
'facet', allow_empty=True)
gamma2_i = domain_i.create_region('Gamma2',
'vertices in (x > %.10f)'
% (max_x - eps_x),
'facet', allow_empty=True)
field_i = Field.from_args('fu', nm.float64, 1, omega_i,
approx_order=order)
output('number of local field DOFs:', field_i.n_nod)
u_i = FieldVariable('u_i', 'unknown', field_i)
v_i = FieldVariable('v_i', 'test', field_i, primary_var_name='u_i')
integral = Integral('i', order=2*order)
mat = Material('m', lam=10, mu=5)
t1 = Term.new('dw_laplace(m.lam, v_i, u_i)',
integral, omega_i, m=mat, v_i=v_i, u_i=u_i)
def _get_load(coors):
val = nm.ones_like(coors[:, 0])
for coor in coors.T:
val *= nm.sin(4 * nm.pi * coor)
return val
def get_load(ts, coors, mode=None, **kwargs):
if mode == 'qp':
return {'val' : _get_load(coors).reshape(coors.shape[0], 1, 1)}
load = Material('load', function=Function('get_load', get_load))
t2 = Term.new('dw_volume_lvf(load.val, v_i)',
integral, omega_i, load=load, v_i=v_i)
eq = Equation('balance', t1 - 100 * t2)
eqs = Equations([eq])
ebc1 = EssentialBC('ebc1', gamma1_i, {'u_i.all' : 0.0})
ebc2 = EssentialBC('ebc2', gamma2_i, {'u_i.all' : 0.1})
pb = Problem('problem_i', equations=eqs, active_only=False)
pb.time_update(ebcs=Conditions([ebc1, ebc2]))
pb.update_materials()
return pb
def verify_save_dof_maps(field, cell_tasks, dof_maps, id_map, options,
verbose=False):
vec = pl.verify_task_dof_maps(dof_maps, id_map, field, verbose=verbose)
order = options.order
mesh = field.domain.mesh
sfield = Field.from_args('aux', nm.float64, 'scalar', field.region,
approx_order=order)
aux = FieldVariable('aux', 'parameter', sfield,
primary_var_name='(set-to-None)')
out = aux.create_output(vec,
linearization=Struct(kind='adaptive',
min_level=order-1,
max_level=order-1,
eps=1e-8))
filename = os.path.join(options.output_dir,
'para-domains-dofs.h5')
if field.is_higher_order():
out['aux'].mesh.write(filename, out=out)
else:
mesh.write(filename, out=out)
out = Struct(name='cells', mode='cell',
data=cell_tasks[:, None, None, None])
filename = os.path.join(options.output_dir,
'para-domains-cells.h5')
mesh.write(filename, out={'cells' : out})
def solve_problem(mesh_filename, options, comm):
order = options.order
rank, size = comm.Get_rank(), comm.Get_size()
output('rank', rank, 'of', size)
stats = Struct()
timer = Timer('solve_timer')
timer.start()
mesh = Mesh.from_file(mesh_filename)
stats.t_read_mesh = timer.stop()
timer.start()
if rank == 0:
cell_tasks = pl.partition_mesh(mesh, size, use_metis=options.metis,
verbose=True)
else:
cell_tasks = None
stats.t_partition_mesh = timer.stop()
output('creating global domain and field...')
timer.start()
domain = FEDomain('domain', mesh)
omega = domain.create_region('Omega', 'all')
field = Field.from_args('fu', nm.float64, 1, omega, approx_order=order)
stats.t_create_global_fields = timer.stop()
output('...done in', timer.dt)
output('distributing field %s...' % field.name)
timer.start()
distribute = pl.distribute_fields_dofs
lfds, gfds = distribute([field], cell_tasks,
is_overlap=True,
save_inter_regions=options.save_inter_regions,
output_dir=options.output_dir,
comm=comm, verbose=True)
lfd = lfds[0]
stats.t_distribute_fields_dofs = timer.stop()
output('...done in', timer.dt)
if rank == 0:
dof_maps = gfds[0].dof_maps
id_map = gfds[0].id_map
if options.verify:
verify_save_dof_maps(field, cell_tasks,
dof_maps, id_map, options, verbose=True)
if options.plot:
ppd.plot_partitioning([None, None], field, cell_tasks, gfds[0],
options.output_dir, size)
output('creating local problem...')
timer.start()
omega_gi = Region.from_cells(lfd.cells, field.domain)
omega_gi.finalize()
omega_gi.update_shape()
pb = create_local_problem(omega_gi, order)
variables = pb.get_variables()
eqs = pb.equations
u_i = variables['u_i']
field_i = u_i.field
stats.t_create_local_problem = timer.stop()
output('...done in', timer.dt)
if options.plot:
ppd.plot_local_dofs([None, None], field, field_i, omega_gi,
options.output_dir, rank)
output('allocating global system...')
timer.start()
sizes, drange = pl.get_sizes(lfd.petsc_dofs_range, field.n_nod, 1)
output('sizes:', sizes)
output('drange:', drange)
pdofs = pl.get_local_ordering(field_i, lfd.petsc_dofs_conn)
output('pdofs:', pdofs)
pmtx, psol, prhs = pl.create_petsc_system(pb.mtx_a, sizes, pdofs, drange,
is_overlap=True, comm=comm,
verbose=True)
stats.t_allocate_global_system = timer.stop()
output('...done in', timer.dt)
output('evaluating local problem...')
timer.start()
state = State(variables)
state.fill(0.0)
state.apply_ebc()
rhs_i = eqs.eval_residuals(state())
# This must be after pl.create_petsc_system() call!
mtx_i = eqs.eval_tangent_matrices(state(), pb.mtx_a)
stats.t_evaluate_local_problem = timer.stop()
output('...done in', timer.dt)
output('assembling global system...')
timer.start()
apply_ebc_to_matrix(mtx_i, u_i.eq_map.eq_ebc)
pl.assemble_rhs_to_petsc(prhs, rhs_i, pdofs, drange, is_overlap=True,
comm=comm, verbose=True)
pl.assemble_mtx_to_petsc(pmtx, mtx_i, pdofs, drange, is_overlap=True,
comm=comm, verbose=True)
stats.t_assemble_global_system = timer.stop()
output('...done in', timer.dt)
output('creating solver...')
timer.start()
conf = Struct(method='cg', precond='gamg', sub_precond='none',
i_max=10000, eps_a=1e-50, eps_r=1e-5, eps_d=1e4, verbose=True)
status = {}
ls = PETScKrylovSolver(conf, comm=comm, mtx=pmtx, status=status)
stats.t_create_solver = timer.stop()
output('...done in', timer.dt)
output('solving...')
timer.start()
psol = ls(prhs, psol)
psol_i = pl.create_local_petsc_vector(pdofs)
gather, scatter = pl.create_gather_scatter(pdofs, psol_i, psol, comm=comm)
scatter(psol_i, psol)
sol0_i = state() - psol_i[...]
psol_i[...] = sol0_i
gather(psol, psol_i)
stats.t_solve = timer.stop()
output('...done in', timer.dt)
output('saving solution...')
timer.start()
u_i.set_data(sol0_i)
out = u_i.create_output()
filename = os.path.join(options.output_dir, 'sol_%02d.h5' % comm.rank)
pb.domain.mesh.write(filename, io='auto', out=out)
gather_to_zero = pl.create_gather_to_zero(psol)
psol_full = gather_to_zero(psol)
if comm.rank == 0:
sol = psol_full[...].copy()[id_map]
u = FieldVariable('u', 'parameter', field,
primary_var_name='(set-to-None)')
filename = os.path.join(options.output_dir, 'sol.h5')
if (order == 1) or (options.linearization == 'strip'):
out = u.create_output(sol)
mesh.write(filename, io='auto', out=out)
else:
out = u.create_output(sol, linearization=Struct(kind='adaptive',
min_level=0,
max_level=order,
eps=1e-3))
out['u'].mesh.write(filename, io='auto', out=out)
stats.t_save_solution = timer.stop()
output('...done in', timer.dt)
stats.t_total = timer.total
stats.n_dof = sizes[1]
stats.n_dof_local = sizes[0]
stats.n_cell = omega.shape.n_cell
stats.n_cell_local = omega_gi.shape.n_cell
if options.show:
plt.show()
return stats
def save_stats(filename, pars, stats, overwrite, rank, comm=None):
out = stats.to_dict()
names = sorted(out.keys())
shape_dict = {'n%d' % ii : pars.shape[ii] for ii in range(pars.dim)}
keys = ['size', 'rank', 'dim'] + list(shape_dict.keys()) + ['order'] + names
out['size'] = comm.size
out['rank'] = rank
out['dim'] = pars.dim
out.update(shape_dict)
out['order'] = pars.order
if rank == 0 and overwrite:
with open(filename, 'w') as fd:
writer = csv.DictWriter(fd, fieldnames=keys)
writer.writeheader()
writer.writerow(out)
else:
with open(filename, 'a') as fd:
writer = csv.DictWriter(fd, fieldnames=keys)
writer.writerow(out)
helps = {
'output_dir' :
'output directory',
'dims' :
'dimensions of the block [default: %(default)s]',
'shape' :
'shape (counts of nodes in x, y, z) of the block [default: %(default)s]',
'centre' :
'centre of the block [default: %(default)s]',
'2d' :
'generate a 2D rectangle, the third components of the above'
' options are ignored',
'order' :
'field approximation order',
'linearization' :
'linearization used for storing the results with approximation order > 1'
' [default: %(default)s]',
'metis' :
'use metis for domain partitioning',
'verify' :
'verify domain partitioning, save cells and DOFs of tasks'
' for visualization',
'plot' :
'make partitioning plots',
'save_inter_regions' :
'save inter-task regions for debugging partitioning problems',
'show' :
'show partitioning plots (implies --plot)',
'stats_filename' :
'name of the stats file for storing elapsed time statistics',
'new_stats' :
'create a new stats file with a header line (overwrites existing!)',
'silent' : 'do not print messages to screen',
'clear' :
'clear old solution files from output directory'
' (DANGEROUS - use with care!)',
}
def main():
parser = ArgumentParser(description=__doc__.rstrip(),
formatter_class=RawDescriptionHelpFormatter)
parser.add_argument('output_dir', help=helps['output_dir'])
parser.add_argument('--dims', metavar='dims',
action='store', dest='dims',
default='1.0,1.0,1.0', help=helps['dims'])
parser.add_argument('--shape', metavar='shape',
action='store', dest='shape',
default='11,11,11', help=helps['shape'])
parser.add_argument('--centre', metavar='centre',
action='store', dest='centre',
default='0.0,0.0,0.0', help=helps['centre'])
parser.add_argument('-2', '--2d',
action='store_true', dest='is_2d',
default=False, help=helps['2d'])
parser.add_argument('--order', metavar='int', type=int,
action='store', dest='order',
default=1, help=helps['order'])
parser.add_argument('--linearization', choices=['strip', 'adaptive'],
action='store', dest='linearization',
default='strip', help=helps['linearization'])
parser.add_argument('--metis',
action='store_true', dest='metis',
default=False, help=helps['metis'])
parser.add_argument('--verify',
action='store_true', dest='verify',
default=False, help=helps['verify'])
parser.add_argument('--plot',
action='store_true', dest='plot',
default=False, help=helps['plot'])
parser.add_argument('--show',
action='store_true', dest='show',
default=False, help=helps['show'])
parser.add_argument('--save-inter-regions',
action='store_true', dest='save_inter_regions',
default=False, help=helps['save_inter_regions'])
parser.add_argument('--stats', metavar='filename',
action='store', dest='stats_filename',
default=None, help=helps['stats_filename'])
parser.add_argument('--new-stats',
action='store_true', dest='new_stats',
default=False, help=helps['new_stats'])
parser.add_argument('--silent',
action='store_true', dest='silent',
default=False, help=helps['silent'])
parser.add_argument('--clear',
action='store_true', dest='clear',
default=False, help=helps['clear'])
options, petsc_opts = parser.parse_known_args()
if options.show:
options.plot = True
comm = pl.PETSc.COMM_WORLD
output_dir = options.output_dir
filename = os.path.join(output_dir, 'output_log_%02d.txt' % comm.rank)
if comm.rank == 0:
ensure_path(filename)
comm.barrier()
output.prefix = 'sfepy_%02d:' % comm.rank
output.set_output(filename=filename, combined=options.silent == False)
output('petsc options:', petsc_opts)
mesh_filename = os.path.join(options.output_dir, 'para.h5')
dim = 2 if options.is_2d else 3
dims = nm.array(eval(options.dims), dtype=nm.float64)[:dim]
shape = nm.array(eval(options.shape), dtype=nm.int32)[:dim]
centre = nm.array(eval(options.centre), dtype=nm.float64)[:dim]
output('dimensions:', dims)
output('shape: ', shape)
output('centre: ', centre)
if comm.rank == 0:
from sfepy.mesh.mesh_generators import gen_block_mesh
if options.clear:
remove_files_patterns(output_dir,
['*.h5', '*.mesh', '*.txt', '*.png'],
ignores=['output_log_%02d.txt' % ii
for ii in range(comm.size)],
verbose=True)
save_options(os.path.join(output_dir, 'options.txt'),
[('options', vars(options))])
mesh = gen_block_mesh(dims, shape, centre, name='block-fem',
verbose=True)
mesh.write(mesh_filename, io='auto')
comm.barrier()
output('field order:', options.order)
stats = solve_problem(mesh_filename, options, comm)
output(stats)
if options.stats_filename:
if comm.rank == 0:
ensure_path(options.stats_filename)
comm.barrier()
pars = Struct(dim=dim, shape=shape, order=options.order)
pl.call_in_rank_order(
lambda rank, comm:
save_stats(options.stats_filename, pars, stats, options.new_stats,
rank, comm),
comm
)
if __name__ == '__main__':
main()

