sfepy.terms.terms_biot module¶
- class sfepy.terms.terms_biot.BiotETHTerm(name, arg_str, integral, region, **kwargs)[source]¶
This term has the same definition as dw_biot_th, but assumes an exponential approximation of the convolution kernel resulting in much higher efficiency. Can use derivatives.
- Definition:
![\begin{array}{l}
\int_{\Omega} \left [\int_0^t \alpha_{ij}(t-\tau)\,p(\tau)) \difd{\tau}
\right]\,e_{ij}(\ul{v}) \mbox{ ,} \\
\int_{\Omega} \left [\int_0^t
\alpha_{ij}(t-\tau) e_{kl}(\ul{u}(\tau)) \difd{\tau} \right] q
\end{array}](../../../_images/math/c01db865e05fe0edb8964623c287b0f08c8c47e6.png)
- Call signature:
dw_biot_eth
(ts, material_0, material_1, virtual, state)(ts, material_0, material_1, state, virtual)- Arguments 1:
ts :
TimeStepperinstancematerial_0 :
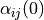
material_1 :
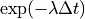 (decay at
(decay at 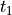 )
)virtual :

state :

- Arguments 2:
ts :
TimeStepperinstancematerial_0 :
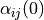
material_1 :
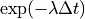 (decay at
(decay at 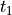 )
)state :

virtual :
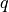
- arg_shapes = {'material_0': 'S, 1', 'material_1': '1, 1', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}¶
- arg_types = (('ts', 'material_0', 'material_1', 'virtual', 'state'), ('ts', 'material_0', 'material_1', 'state', 'virtual'))¶
- modes = ('grad', 'div')¶
- name = 'dw_biot_eth'¶
- class sfepy.terms.terms_biot.BiotStressTerm(name, arg_str, integral, region, **kwargs)[source]¶
Evaluate Biot stress tensor.
It is given in the usual vector form exploiting symmetry: in 3D it has 6 components with the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in
2D it has 3 components with the indices ordered as
, in
2D it has 3 components with the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) .
.Supports ‘eval’, ‘el_avg’ and ‘qp’ evaluation modes.
- Definition:
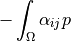
- Call signature:
ev_biot_stress
(material, parameter)- Arguments:
material :
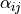
parameter :

- arg_shapes = {'material': 'S, 1', 'parameter': 1}¶
- arg_types = ('material', 'parameter')¶
- integration = 'cell'¶
- name = 'ev_biot_stress'¶
- class sfepy.terms.terms_biot.BiotTHTerm(name, arg_str, integral, region, **kwargs)[source]¶
Fading memory Biot term. Can use derivatives.
- Definition:
![\begin{array}{l}
\int_{\Omega} \left [\int_0^t \alpha_{ij}(t-\tau)\,p(\tau)) \difd{\tau}
\right]\,e_{ij}(\ul{v}) \mbox{ ,} \\
\int_{\Omega} \left [\int_0^t
\alpha_{ij}(t-\tau) e_{kl}(\ul{u}(\tau)) \difd{\tau} \right] q
\end{array}](../../../_images/math/c01db865e05fe0edb8964623c287b0f08c8c47e6.png)
- Call signature:
dw_biot_th
(ts, material, virtual, state)(ts, material, state, virtual)- Arguments 1:
ts :
TimeStepperinstancematerial :
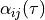
virtual :

state :

- Arguments 2:
ts :
TimeStepperinstancematerial :
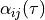
state :

virtual :
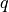
- arg_shapes = {'material': '.: N, S, 1', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}¶
- arg_types = (('ts', 'material', 'virtual', 'state'), ('ts', 'material', 'state', 'virtual'))¶
- modes = ('grad', 'div')¶
- name = 'dw_biot_th'¶
- class sfepy.terms.terms_biot.BiotTerm(name, arg_str, integral, region, **kwargs)[source]¶
Biot coupling term with
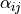 given in:
given in:vector form exploiting symmetry - in 3D it has the indices ordered as
![[11, 22, 33, 12, 13, 23]](../../../_images/math/831e68247b7b81f4648d22336a8bd761038d0416.png) , in 2D it has
the indices ordered as
, in 2D it has
the indices ordered as ![[11, 22, 12]](../../../_images/math/f930f08c378137d074ca533e6d938267b04d560b.png) ,
,matrix form - non-symmetric coupling parameter.
Corresponds to weak forms of Biot gradient and divergence terms. Can be evaluated. Can use derivatives.
- Definition:
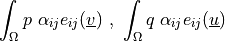
- Call signature:
dw_biot
(material, virtual, state)(material, state, virtual)(material, parameter_v, parameter_s)- Arguments 1:
material :
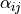
virtual :

state :

- Arguments 2:
material :
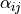
state :

virtual :
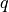
- Arguments 3:
material :
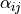
parameter_v :

parameter_s :

- arg_shapes = [{'material': 'S, 1', 'parameter_s': 1, 'parameter_v': 'D', 'state/div': 'D', 'state/grad': 1, 'virtual/div': (1, None), 'virtual/grad': ('D', None)}, {'material': 'D, D'}]¶
- arg_types = (('material', 'virtual', 'state'), ('material', 'state', 'virtual'), ('material', 'parameter_v', 'parameter_s'))¶
- modes = ('grad', 'div', 'eval')¶
- name = 'dw_biot'¶